
الارتباط مفهوم أساسي في الإحصاء وتحليل البيانات، حيث يساعد على فهم العلاقة بين متغيرين. وفي حين أنه غالباً ما يتم تسليط الضوء على الارتباطات الموجبة أو السالبة القوية، فإن الارتباط الصفري لا يقل أهمية.
وهذا يعني عدم وجود علاقة خطية بين المتغيرين. بعبارة أخرى، لا تتنبأ التغيرات في أحد المتغيرين بالتغيرات في المتغير الآخر.
في هذه المدونة، سنستكشف مفهوم الارتباط الصفري، وسنقدم تعريفًا واضحًا وأمثلة توضيحية وطرق تحديده.
ما هو الارتباط الصفري؟
الارتباط الصفري هو مصطلح إحصائي يصف حالة لا توجد فيها علاقة خطية بين متغيرين. عندما يكون الارتباط بين متغيّرين ارتباطاً صفرياً، فإن التغيّرات في أحد المتغيّرين لا تتنبأ بالتغيّرات في المتغيّر الآخر. وفي هذه الحالة يكون معامل الارتباط، الذي يقيس درجة واتجاه العلاقة بين المتغيرين، يساوي صفرًا تمامًا.
يعد فهم هذا الارتباط مهمًا في التحليل الإحصائي لأنه يساعد في تحديد المتغيرات التي لا توجد علاقة تنبؤية بينها وبين بعضها البعض، وهو أمر بالغ الأهمية عند بناء النماذج الإحصائية أو تفسير أنماط البيانات.
ما أهمية الارتباط الصفري؟
يعد الارتباط الصفري مفهومًا مهمًا في الإحصاء وتحليل البيانات لعدة أسباب مثل:
يحدد الاستقلالية
فهو يساعد على تحديد المتغيرات المستقلة خطياً عن بعضها البعض. إذا كان الارتباط بين متغيّرين لا يوجد بينهما أي ارتباط، فإن التغييرات في أحد المتغيّرين لا توفر أي معلومات حول التغييرات في المتغيّر الآخر. وهذا أمر بالغ الأهمية لفهم بنية البيانات والعلاقات (أو عدم وجودها) بين المتغيرات.
يحسن النماذج الإحصائية
في تحليل الانحدار والنماذج الإحصائية الأخرى، يمكن أن يؤدي تضمين المتغيرات التي لها هذا الارتباط بالمتغير التابع إلى إضافة ضوضاء وتقليل القدرة التنبؤية للنموذج. من خلال تحديد واستبعاد مثل هذه المتغيرات، يمكن تبسيط النماذج وجعلها أكثر كفاءة، مما يؤدي إلى تحسين الأداء وقابلية التفسير.
يساعد هذا الارتباط على تجنب التفسير الخاطئ
إن فهم هذا الارتباط يمنع سوء تفسير البيانات.
- على سبيل المثال، قد يستنتج الباحث خطأً وجود علاقة بين متغيرين بناءً على الحدس أو الملاحظات الأولية.
يوضح حساب معامل الارتباط وإيجاد أنه يساوي صفرًا أنه لا توجد علاقة خطية، مما يجنبنا استنتاجات خاطئة.
يسلط الضوء على العلاقات غير الخطية
يسلط الضوء على إمكانية وجود علاقات غير خطية. إذا كان الارتباط بين متغيّرين لا يعني بالضرورة أنهما غير مترابطين؛ فقد تكون بينهما علاقة معقدة وغير خطية. يمكن أن يؤدي إدراك ذلك إلى إجراء مزيد من التحقيق باستخدام طرق أخرى، مثل الانحدار غير الخطي أو تحويل البيانات.
يساعد الارتباط في توجيه التصميم التجريبي
في التصميم التجريبي، يمكن أن تؤدي معرفة المتغيرات التي لها ارتباط صفري إلى توجيه اختيار المتغيرات التي يجب تضمينها أو التحكم فيها. ويساعد ذلك في تصميم تجارب أكثر قوة حيث يتم تقليل تأثير المتغيرات غير ذات الصلة إلى الحد الأدنى، مما يؤدي إلى نتائج أوضح وأكثر موثوقية.
يفهم السلوك المتغير
يوفر نظرة ثاقبة لسلوك المتغيرات في مجموعة البيانات. في التحليل المالي، يمكن أن يساعد فهم الأصول التي لا ترتبط ببعضها البعض في تنويع المحفظة الاستثمارية، حيث يمكن أن يؤدي الجمع بين هذه الأصول إلى تقليل المخاطر الإجمالية.
يدعم اختبار الفرضيات
في اختبار الفرضيات، غالبًا ما يكون هذا الارتباط فرضية لاغية.
- على سبيل المثال، في اختبار ما إذا كان هناك متغيران مرتبطان أم لا، قد تنص الفرضية الفارغة على أن الارتباط بينهما يساوي صفرًا.
يساعد تحديد ما إذا كان ذلك صحيحاً أو خاطئاً في التحقق من صحة الفرضيات أو دحضها.
ما هي أمثلة الارتباط الصفري؟
يمكن العثور على أمثلة على هذا الارتباط، حيث لا تتوافق التغيرات في أحد المتغيرات مع التغيرات في متغير آخر، في مجالات مختلفة مثل
مجال البحث
مثال: عدد المنشورات العلمية ونكهة الآيس كريم المفضلة
تبحث دراسة في العلاقة بين عدد المنشورات العلمية للباحثين ونكهة الآيس كريم المفضلة لديهم.
لا توجد علاقة منطقية بين عدد الأوراق العلمية التي ينشرها الباحث وتفضيله لنكهة آيس كريم معينة. ونتيجة لذلك، من المتوقع أن يظهر هذا الارتباط بين هذين المتغيرين.
مجال التعليم
مثال: حجم حذاء الطلاب ودرجاتهم في الرياضيات
تبحث دراسة تربوية فيما إذا كانت هناك أي علاقة بين أحجام أحذية الطلاب ودرجاتهم في مادة الرياضيات.
حجم الحذاء هو خاصية جسدية ليس لها أي تأثير على الأداء الأكاديمي للطالب في الرياضيات. ولذلك، من المرجح أن تكون العلاقة بين حجم الحذاء ودرجات الرياضيات صفراً.
مجال الرعاية الصحية
مثال: فصيلة الدم والإصابة بنزلات البرد الشائعة
تبحث دراسة للرعاية الصحية فيما إذا كانت هناك علاقة بين فصيلة دم الشخص وعدد المرات التي يصاب فيها بنزلة البرد في السنة.
لا ترتبط فصيلة الدم بتكرار الإصابة بنزلات البرد، والتي تتأثر بعوامل أخرى مختلفة مثل التعرض للفيروسات وقوة الجهاز المناعي. وبالتالي، من المتوقع أن يكون الارتباط بين فصيلة الدم ومعدل الإصابة بنزلات البرد صفراً.
كيفية تحديد الارتباط الصفري؟
سنستكشف هنا كيفية تحديد هذا الارتباط من خلال الفحص البصري، والحساب الإحصائي، واختبار الفرضيات، والتحليل السياقي.
1. الفحص البصري باستخدام المخططات المبعثرة
تعتبر مخططات التبعثر أداة فعالة لتقييم العلاقة بين متغيرين بصرياً.
إنشاء مخطط مبعثر:
- ضع أحد المتغيرين على المحور س والآخر على المحور ص.
- ابحث عن أي اتجاه أو نمط يمكن تمييزه في نقاط البيانات.
تحديد الارتباط:
- إذا كانت النقاط مبعثرة بشكل عشوائي دون وجود اتجاه واضح (لا تصاعدي ولا تنازلي)، فهذا يشير إلى وجود ارتباط.
- يشير التشتت العشوائي إلى أنه لا يوجد خط (سواء كان مستقيمًا أو منحنيًا) يمكن أن يلائم نقاط البيانات بشكل جيد.
مثال:
- أحجام أحذية الطلاب مقابل درجات الرياضيات: إذا قمت برسم أحجام الأحذية مقابل درجات الرياضيات ورأيت تشتتاً عشوائياً للنقاط بدون اتجاه، فهذا يشير إلى عدم وجود ارتباط.
2. حساب معامل الارتباط
معامل ارتباط بيرسون (r) هو المقياس الأكثر شيوعًا للارتباط الخطي.
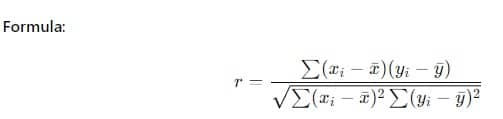
الخطوات:
- اجمع نقاط البيانات المزدوجة للمتغيرين.
- أوجد الوسط الحسابي (المتوسط) لكل متغير.
- احسب مدى بُعد كل نقطة بيانات عن الوسط الحسابي.
- اضرب الانحرافات لكل زوج واجمع حواصل الضرب.
- استخدم الصيغة لإيجاد معامل الارتباط.
تفسير الارتباط:
القيمة القريبة من الصفر: إذا كانت قيمة ر ص قريبة من الصفر، فإنها تشير إلى وجود علاقة خطية ضئيلة أو معدومة بين المتغيرات.
مثال:
- مقاسات الأحذية ودرجات الرياضيات: إذا كانت قيمة ر المحسوبة تساوي تقريبًا 0، فهذا يؤكد الارتباط الصفري.
3. إجراء اختبار الفرضية
يمكن أن يحدد اختبار الفرضية الإحصائية ما إذا كان معامل الارتباط الملاحظ يختلف اختلافًا كبيرًا عن الصفر.
الخطوات:
- الفرضية الفارغة: افترض أن معامل الارتباط يساوي صفرًا.
- الفرضية البديلة: افترض أن معامل الارتباط ليس صفراً.
- حساب إحصائية الاختبار: استخدم اختبار t-test لمعامل الارتباط.
- تحديد قيمة p: قارن قيمة p بمستوى دلالة (على سبيل المثال، 0.05).
الارتباط الصفري:
- إذا كانت قيمة p أكبر من مستوى الدلالة، فلا ترفض الفرضية الفارغة، مما يشير إلى أن الارتباط لا يختلف اختلافًا كبيرًا عن الصفر.
مثال:
- فصيلة الدم والإصابة بنزلات البرد الشائعة: اختبار العلاقة بين فصيلة الدم والإصابة بنزلات البرد الشائعة، إذا كانت قيمة p عالية، فهذا يشير إلى أن أي ارتباط ملاحظ ليس ذا دلالة إحصائية، مما يدعم وجود ارتباط صفري.
4. فهم التحليل السياقي
إن فهم السياق والخلفية النظرية للمتغيرات أمر ضروري لتفسير نتائج الارتباط.
الخطوات:
- فحص المتغيرات: النظر في طبيعة المتغيرات والعلاقات المتوقعة بين المتغيرات.
- تطبيق معرفة المجال: استخدام المعرفة من المجال لافتراض ما إذا كانت العلاقة متوقعة أم لا.
الارتباط الصفري:
- إذا كانت النظرية والأبحاث السابقة تشير إلى عدم وجود علاقة منطقية، فإن هذا يدعم اكتشاف هذا الارتباط.
مثال:
- فصيلة الدم والإصابة بنزلات البرد الشائعة: إن معرفة أن فصيلة الدم لا تؤثر على القابلية للإصابة بنزلات البرد الشائعة يدعم تفسير عدم وجود علاقة إذا وجدت.
الارتباط السالب مقابل الارتباط الموجب مقابل الارتباط الصفري
الارتباط هو مقياس إحصائي يصف قوة العلاقة بين متغيرين واتجاهها. فيما يلي شرح مفصل للارتباط السالب والموجب والارتباط الصفري:
الارتباط الإيجابي
- التعريف: يحدث الارتباط الموجب عندما يتحرك متغيران في نفس الاتجاه. فكلما زاد أحد المتغيِّرين، زاد المتغيِّر الآخر أيضًا، وكلما انخفض أحد المتغيِّرين، انخفض الآخر أيضًا.
- مثال: العلاقة بين الطول والوزن. بشكل عام، كلما زاد طول الشخص، يميل وزنه أيضًا إلى الزيادة.
- التمثيل البياني: في مخطط التبعثر، تميل النقاط إلى التجمع حول خط ينحدر لأعلى من اليسار إلى اليمين.
الارتباط السالب
- التعريف: يحدث الارتباط السالب عندما يتحرك متغيران في اتجاهين متعاكسين. فكلما زاد أحد المتغيرين، انخفض المتغير الآخر، والعكس صحيح.
- مثال: العلاقة بين مقدار الوقت المستغرق في المذاكرة وعدد الأخطاء التي يتم ارتكابها في الاختبار. بشكل عام، كلما زاد الوقت المستغرق في المذاكرة، انخفض عدد الأخطاء.
- التمثيل البياني: في مخطط التبعثر، تميل النقاط إلى التجمع حول خط ينحدر لأسفل من اليسار إلى اليمين.
الارتباط الصفري
- التعريف: يشير إلى عدم وجود علاقة بين المتغيرين. فالتغيرات في أحد المتغيرين لا تتنبأ بالتغيرات في المتغير الآخر.
- مثال: العلاقة بين حجم حذاء الشخص وحاصل ذكائه (IQ). لا توجد علاقة منطقية بين هذين المتغيرين.
- التمثيل البياني: في مخطط التبعثر، يتم توزيع النقاط بشكل عشوائي دون وجود نمط أو ميل واضح.
كيف يمكن لـ QuestionPro المساعدة في تحليل الارتباط؟
تقدم QuestionPro، وهي منصة قوية لاستطلاعات الرأي، أدوات شاملة لتسهيل تحليل الارتباط بفعالية. إليك كيف يمكن أن تساعدك QuestionPro في إجراء تحليل الارتباط:
جمع البيانات دون عناء
تعمل QuestionPro على تبسيط عملية جمع البيانات من خلال أدوات إنشاء الاستبيانات سهلة الاستخدام. يمكنك تصميم الاستبيانات وتوزيعها لجمع البيانات الكمية عن مختلف المتغيرات ذات الأهمية. تدعم المنصة أنواعاً مختلفة من الأسئلة، مما يتيح لك الحصول على بيانات مفصلة وذات صلة بكفاءة.
التحليل الآلي للبيانات
بمجرد جمع البيانات، يوفر QuestionPro أدوات تحليل مدمجة لتحليل الارتباط. يمكنك بسهولة حساب الارتباطات التي تقيس قوة العلاقة الخطية بين متغيرين واتجاهها. يتراوح معامل الارتباط الخطي من -1 إلى 1، حيث:
- 1 تشير إلى وجود ارتباط موجب تام.
- -1 تشير إلى وجود ارتباط سالب تام.
- 0 يشير إلى عدم وجود ارتباط.
التمثيل المرئي
يوفر QuestionPro أدوات تصور لمساعدتك في تفسير نتائج تحليل الارتباط. يمكن إنشاء مخططات مبعثرة ومصفوفات الارتباط لتوفير تمثيل بياني واضح للعلاقات بين المتغيرات. هذه الأداة المرئية المساعدة ضرورية لتحديد الاتجاهات والأنماط بسرعة.
تحديد الأنماط والاتجاهات
باستخدام تحليل الارتباط الخاص ببرنامج QuestionPro، لاحظ الباحثون وجود ارتباط (موجب أو سالب أو صفر) بين المتغيرات:
- ارتباط موجب: يتحرك كلا المتغيرين في نفس الاتجاه. على سبيل المثال، قد ترتبط زيادة الإنفاق الإعلاني بزيادة المبيعات.
- الارتباط السالب: تميل المتغيرات إلى التحرك في اتجاهين متعاكسين. على سبيل المثال، قد ترتبط زيادة الوقت أمام الشاشة بانخفاض الأداء الأكاديمي.
- الارتباط الصفري: لا توجد علاقة بين المتغيرات. على سبيل المثال، قد لا يرتبط عدد سنوات الدراسة في المدرسة بعدد الحروف في اسم الشخص.
التطبيقات العملية
يمكن استخدام تحليل الارتباط في QuestionPro في العديد من التطبيقات العملية، مثل:
- أبحاث السوق: قياس فعالية الحملات التسويقية من خلال ربط الإنفاق الإعلاني بأداء المبيعات.
- الرعاية الصحية: تقييم العلاقة بين استخدام الأدوية ونتائج المرضى، مثل مستويات ضغط الدم.
- التعليم: تحديد تأثير عادات الدراسة على الأداء الأكاديمي من خلال الربط بين ساعات الدراسة والدرجات.
استنتاج
يشير الارتباط الصفري بين متغيرين إلى عدم وجود علاقة خطية، مما يشير إلى أن التغيرات في أحد المتغيرين لا تتوافق مع التغيرات في متغير آخر. من خلال حساب معاملات الارتباط وتصور البيانات من خلال مخططات التبعثر، يمكن للباحثين أن يحددوا بدقة ما إذا كانت المتغيرات مترابطة أو مترابطة إيجابياً أو مترابطة سلبياً أو تظهر هذا الارتباط.
يوفر لك استخدام QuestionPro لتحليل الارتباط في استبياناتك طريقة فعالة للكشف عن العلاقات المفيدة بين المتغيرات. من خلال استكشاف واجهة QuestionPro البديهية، والأدوات التحليلية المتقدمة، وميزات إعداد التقارير الشاملة، يمكنك إجراء تحليل الارتباط بكفاءة واستخلاص رؤى قيمة من بياناتك. اتصل بـ QuestionPro اليوم لمزيد من المعلومات!







