
معامل ارتباط سبيرمان: التعريف
معامل ارتباط رتبة سبيرمان أو معامل ارتباط سبيرمان هو مقياس غير معلمي لارتباط الرتبة (الاعتماد الإحصائي للترتيب بين متغيرين).
سميت على اسم تشارلز سبيرمان ، وغالبا ما يشار إليها بالحرف اليوناني ” ρ” (rho) وتستخدم بشكل أساسي لتحليل البيانات.
يقيس قوة واتجاه الارتباط بين متغيرين مرتبين. ولكن قبل أن نتحدث عن معامل ارتباط سبيرمان ، من المهم أن نفهم ارتباط بيرسون أولا. ارتباط بيرسون هو مقياس إحصائي لقوة العلاقة الخطية بين البيانات المقترنة.
لحساب واختبار أهمية متغير الترتيب ، فإنه يتطلب افتراض البيانات التالية ليكون صحيحا:
- مستوى الفاصل الزمني أو النسبة
- ذات الصلة الخطية
- ثنائي المتغير الموزع
إذا كانت بياناتك لا تفي بالافتراضات المذكورة أعلاه ، فستحتاج إلى معامل سبيرمان. من الضروري معرفة الوظيفة الرتيبة لفهم معامل ارتباط سبيرمان. الدالة الرتيبة هي دالة إما لا تنقص أبدا أو لا تزيد أبدا لأنها زيادة متغيرة مستقلة. يمكن شرح وظيفة رتيبة باستخدام الصورة أدناه:
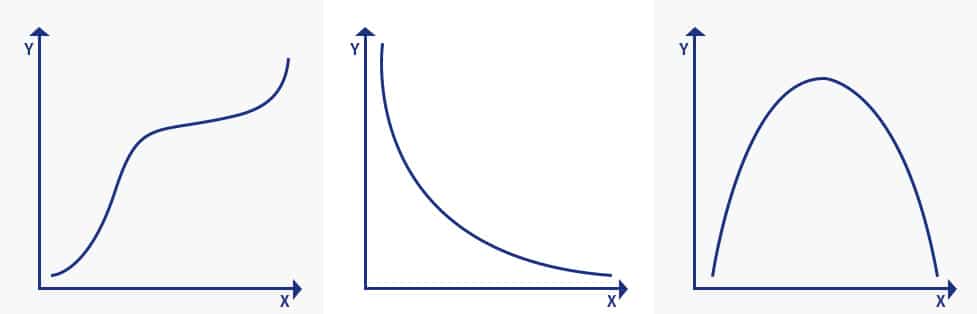
تشرح الصورة ثلاثة مفاهيم في الوظيفة الرتيبة:
- زيادة رتيبة: عندما يزداد المتغير “x” ولا ينخفض المتغير “y” أبدا.
- يتناقص رتابة: عندما يزداد المتغير “x” ولكن المتغير “y” لا يزيد أبدا
- غير رتيب: عندما يزداد المتغير “x” ويزيد المتغير “y” أحيانا وينقص أحيانا.
العلاقة الأحادية أقل تقييدا عند مقارنتها بالعلاقة الخطية المستخدمة في معامل بيرسون. على الرغم من أن الرتابة ليست الشرط النهائي لمعامل ارتباط سبيرمان ، إلا أنه لن يكون من المفيد متابعة ارتباط سبيرمان دون تحديد قوة واتجاه العلاقة الرتيبة إذا كان من المعروف بالفعل أن العلاقة بين المتغير غير أحادية التوتر.
تعرف على المزيد: تحليل العشب مع أمثلة
معامل ارتباط سبيرمان: الصيغة والحساب مع المثال
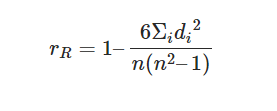 هنا،
هنا،
n = عدد نقاط البيانات للمتغيرين
di= الفرق في رتب عنصر “ith”
يمكن أن يأخذ معامل سبيرمان ، ⍴ ، قيمة تتراوح بين +1 إلى -1 حيث ،
- تعني قيمة ⍴ +1 ارتباطا مثاليا للرتبة
- تعني القيمة ⍴ 0 عدم وجود ارتباط للرتب
- تعني القيمة ⍴ -1 ارتباطا سلبيا مثاليا بين الرتب.
كلما اقتربنا من قيمة ⍴ إلى 0 ، كان الارتباط بين الرتبتين أضعف.
يجب أن نكون قادرين على ترتيب البيانات قبل متابعة معامل ارتباط رتبة سبيرمان. من المهم ملاحظة ما إذا كانت زيادة متغير واحد ، فإن المتغير الآخر يتبع علاقة رتيبة.
في كل مستوى ، ستحتاج إلى مقارنة قيم المتغيرين. إليك كيفية عمل الحسابات:
تم ذكر درجات 9 طلاب في التاريخ والجغرافيا في الجدول أدناه.
الخطوة 1- إنشاء جدول للبيانات التي تم الحصول عليها.
الخطوة 2- ابدأ بترتيب مجموعتي البيانات. يمكن تحقيق ترتيب البيانات عن طريق تعيين الترتيب “1” لأكبر رقم في العمود ، و “2” إلى ثاني أكبر رقم وهكذا دواليك. عادة ما تحصل أصغر قيمة على أدنى ترتيب. يجب أن يتم ذلك لكلتا المجموعتين من القياسات.
الخطوة 3- أضف عمودا ثالثا d إلى مجموعة البيانات الخاصة بك ، حيث يشير d هنا إلى الفرق بين الرتب. على سبيل المثال ، إذا كانت رتبة الفيزياء للطالب الأول هي 3 ورتبة الرياضيات هي 5 ، فإن الفرق في الترتيب هو 3. في العمود الرابع ، قم بتربيع قيم d الخاصة بك.
| تاريخ | رتبة | جغرافيا | رتبة | d | د مربع |
| 35 | 3 | 30 | 5 | 2 | 4 |
| 23 | 5 | 33 | 3 | 2 | 4 |
| 47 | 1 | 45 | 2 | 1 | 1 |
| 17 | 6 | 23 | 6 | 0 | 0 |
| 10 | 7 | 8 | 8 | 1 | 1 |
| 43 | 2 | 49 | 1 | 1 | 1 |
| 9 | 8 | 12 | 7 | 1 | 1 |
| 6 | 9 | 4 | 9 | 0 | 0 |
| 28 | 4 | 31 | 4 | 0 | 0 |
| 12 |
الخطوة 4- اجمع كل قيم مربع d الخاصة بك ، وهي 12 (∑d مربع)
الخطوة 5- أدخل هذه القيم في الصيغة
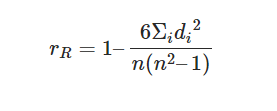
= 1- (6 * 12) / (9 (81-1))
= 1-72 / 720
= 1-01
= 0.9
ارتباط رتبة سبيرمان لهذه البيانات هو 0.9 وكما ذكر أعلاه إذا كانت قيمة ⍴ تقترب من +1 ، فلديهم ارتباط مثالي للرتبة.
تعرف على المزيد: التحليل الموحد – التعريف والأنواع والمثال والخوارزمية والنموذج
كيفية إجراء معامل الارتباط مع QuestionPro
في هذا القسم ، ستتعلم كيف يمكنك تشغيل معامل ارتباط رتبة سبيرمان للاستطلاع الخاص بك.
الخطوة 1: انتقل إلى الاستطلاعات الخاصة بي →تحديد استطلاع→تحليلات
الخطوة 2: انقر فوق التحليل الارتباطي تحت التحليل
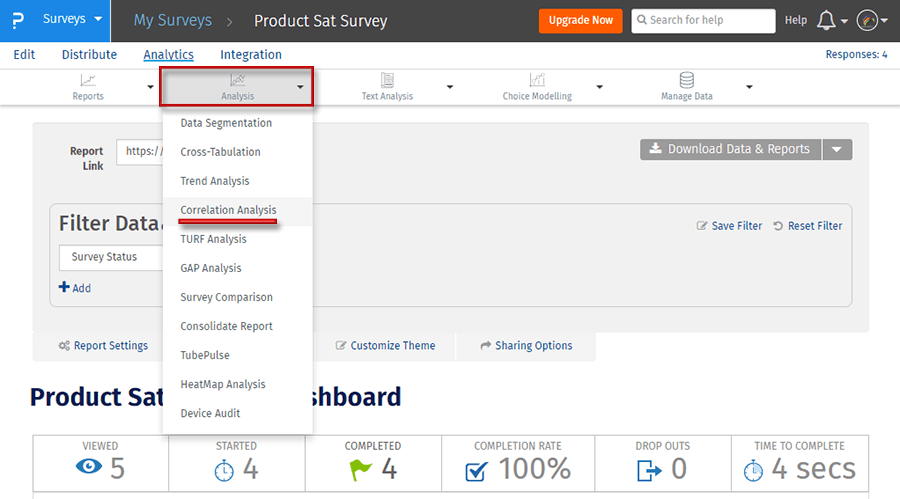
الخطوة 3: انقر على زر إنشاء معامل سبيرمان للحصول على تقرير مفصل
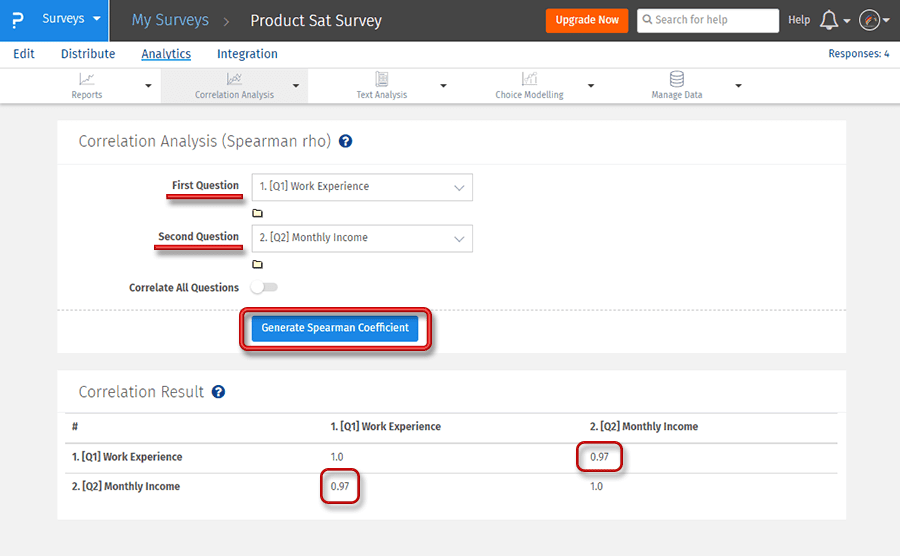
في المثال أعلاه ، يتم استخدام معامل سبيرمان للارتباط لمعرفة العلاقة بين المتغيرين ، خبرة العمل والدخل الشهري. الفكرة العامة هي أن الدخل الشهري يجب أن يزداد مع خبرة العمل ، مما يعني أنه يجب أن يكون هناك ارتباط إيجابي بين المتغيرين وهو ما تثبته قيمة rs وهي 0.97
تعرف على المزيد: تحليل GAP – التعريف والطريقة والقالب مع مثال







