Korrelationsmatrix: Was ist sie, wie funktioniert sie & Beispiele

Haben Sie sich jemals gefragt, wie sich Dinge wie Ihr Budget, Ihr Umsatz oder die Kundenzufriedenheit gegenseitig beeinflussen? Was wäre, wenn es eine einfache Möglichkeit gäbe, diese Zusammenhänge auf einen Blick zu erkennen? Der beste Weg ist eine Korrelationsmatrix. Sie ist wie ein Spickzettel, mit dem Sie verborgene Beziehungen in Ihren Daten aufdecken können. Sie wird häufig in Bereichen wie Finanzen, Wirtschaft, Psychologie und Biologie verwendet, weil sie den Menschen hilft zu verstehen, wie verschiedene Dinge miteinander in Beziehung stehen.

Um gute Entscheidungen auf der Grundlage von Daten zu treffen, müssen Sie wissen, wie man eine Korrelationsmatrix liest und verwendet. Sie zeigt die Variablen in Zeilen und Spalten an. Der Korrelationskoeffizient wird in jede Zelle einer Tabelle geschrieben.

In diesem Blog zeigen wir Ihnen, wie eine Korrelationsmatrix funktioniert und geben Ihnen einige Beispiele, damit Sie herausfinden, wie Sie sie zur Datenanalyse verwenden können.

Was ist eine Korrelationsmatrix?

Eine Korrelationsmatrix ist eine Tabelle mit Korrelationskoeffizienten, die die Stärke und Richtung der Beziehungen zwischen Variablen messen.

Die Matrix zeigt, wie alle möglichen Wertepaare in einer Tabelle zueinander in Beziehung stehen. Sie ist ein leistungsfähiges Werkzeug, um einen großen Datensatz zusammenzufassen und Muster in den Daten zu finden und darzustellen.

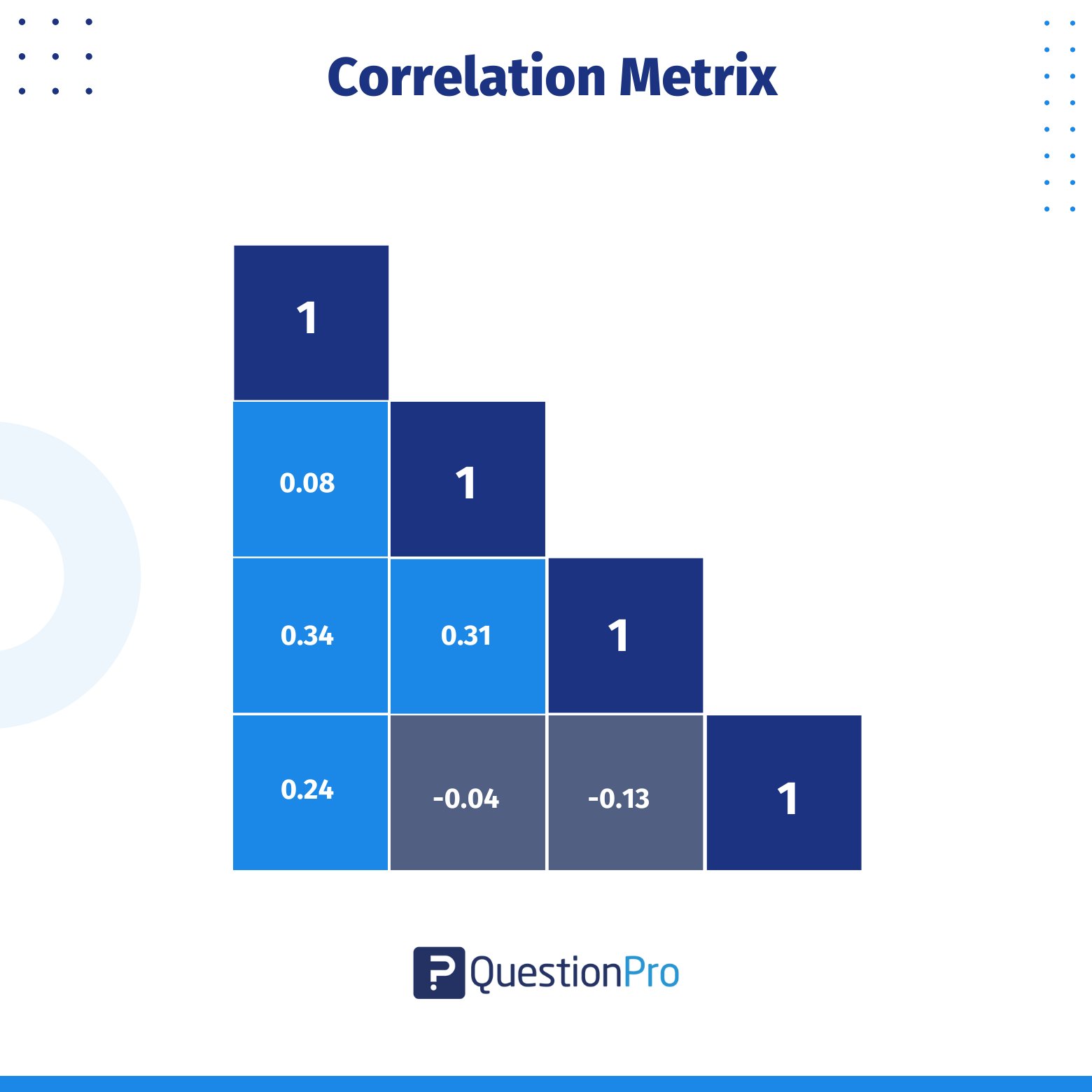
Sie wird oft in Form einer Tabelle dargestellt, in der jede Variable sowohl in den Zeilen als auch in den Spalten aufgeführt ist und der Korrelationskoeffizient zwischen jedem Variablenpaar in jeder Zelle steht.

Der Korrelationskoeffizient reicht von -1 bis +1, wobei -1 für eine perfekte negative Korrelation, +1 für eine perfekte positive Korrelation und 0 für eine Nullkorrelation zwischen den Variablen steht.

Wann wird eine Korrelationsmatrix verwendet?

Eine Korrelationsmatrix ist ein wertvolles Instrument, um Einblicke in Ihren Datensatz zu gewinnen. Wenn Sie zum Beispiel versuchen, den Preis eines Autos auf der Grundlage von Faktoren wie Kraftstofftyp, Getriebe oder Alter vorherzusagen, hilft Ihnen die Korrelationsmatrix, die Beziehungen zwischen diesen Variablen zu verstehen.

So funktioniert die Matrix:

• Ein Wert von 1 weist auf eine starke positive Beziehung zwischen zwei Variablen hin.
• Ein Wert von 0 bedeutet, dass es keine Beziehung zwischen ihnen gibt.
• Ein Wert von -1 signalisiert eine stark negative oder umgekehrte Beziehung.

Mithilfe einer Korrelationsmatrix können Sie die Zusammenhänge in Ihren Daten leicht analysieren und visualisieren. Dies macht sie zu einem wichtigen Schritt für Datenwissenschaftler, bevor sie Modelle für maschinelles Lernen erstellen. Wenn Sie verstehen, welche Variablen miteinander korreliert sind, können Sie die einflussreichsten Faktoren für Ihr Modell identifizieren.

Die Matrix bietet eine Reihe von Werten zwischen -1 und 1, mit denen Sie die Stärke und Richtung der Beziehungen zwischen den Variablen bestimmen können.

Wie funktioniert die Korrelationsmatrix?

Die folgende Formel wird verwendet, um den Korrelationskoeffizienten zwischen zwei Variablen zu berechnen:

r = (nΣXY – ΣXΣY) / sqrt((nΣX^2 – (ΣX)^2)(nΣY^2 – (ΣY)^2))

Wo:

• r = Korrelationskoeffizient
• n = Anzahl der Beobachtungen
• ΣXY = Summe des Produkts jedes Paars der entsprechenden Beobachtungen der beiden Variablen
• ΣX = Summe der Beobachtungen der ersten Variablen
• ΣY = Summe der Beobachtungen der zweiten Variablen
• ΣX^2 = Summe der Quadrate der Beobachtungen der ersten Variablen
• ΣY^2 = Summe der Quadrate der Beobachtungen der zweiten Variablen

Der resultierende Korrelationskoeffizient variiert von -1 bis +1, wobei -1 für eine perfekte negative Korrelation, +1 für eine perfekte positive Korrelation und 0 für keine Korrelation zwischen den Variablen steht.

• Sie können damit feststellen, welche Variablen signifikant miteinander verbunden sind und welche schlecht oder gar nicht korreliert sind. Diese Informationen können genutzt werden, um Prognosen und fundierte Urteile auf der Grundlage von Fakten zu erstellen.
• So können Sie schnell und einfach erkennen, wie die verschiedenen Variablen miteinander verbunden sind. Variablen, die dazu neigen, gemeinsam zu steigen oder zu fallen, haben hohe positive Korrelationskoeffizienten. Variablen, die sich in entgegengesetzter Richtung nach oben oder unten entwickeln, haben hohe negative Korrelationskoeffizienten.
• Sie ist wichtig, um Muster und Beziehungen zwischen Variablen zu finden. Sie kann auch verwendet werden, um Vorhersagen und Entscheidungen auf der Grundlage von Daten zu treffen. Niedrige Korrelationskoeffizienten zeigen, dass die beiden Variablen keine starke Beziehung zueinander haben.

Die wichtigsten Punkte der Korrelationsmatrix

Die Korrelationsmatrix mag wie ein etwas abstraktes Konzept mit vielen Variationen erscheinen, insbesondere wenn wir uns die verschiedenen Arten von statistischen Matrizen ansehen, die es gibt. Es gibt jedoch bestimmte Merkmale, die eine Korrelationsmatrix funktional und effektiv machen.

Nachfolgend finden Sie die wichtigsten Punkte:

• Beziehungen zwischen Variablen: Mit Hilfe der Korrelationsmatrix können Sie feststellen, wie zwei oder mehr Variablen zueinander in Beziehung stehen oder voneinander abhängen.
• Leicht zu lesende Tabelle: Die Tabelle ist in einem Tabellenformat dargestellt, das es leicht macht, sie zu lesen, zu verstehen und Muster zu finden, um vorherzusagen, was in Zukunft passieren wird.
• Daten-Zusammenfassung: Die Idee hilft dabei, die Daten zusammenzufassen und zu soliden Schlussfolgerungen zu kommen, die den Anlegern helfen, bessere Entscheidungen darüber zu treffen, wo sie ihr Geld anlegen sollen.
• Werkzeug-Optionen: Sie können Excel oder fortgeschrittenere Tools wie SPSS und das von Python gesteuerte Pandas verwenden, um die Matrix effektiv zu erstellen.

Zusammenfassend lässt sich sagen, dass eine Korrelationsmatrix ein hilfreiches Instrument ist, um schnell zu verstehen, wie verschiedene Variablen zusammenhängen, was Ihnen helfen kann, datengestützte Entscheidungen zu treffen.

Beispiel für die Korrelationsmatrix

Lassen Sie uns an einem Beispiel sehen, wie eine Korrelationsmatrix beim Lesen und Verstehen eines Datensatzes mit vier Variablen helfen kann: Alter, Einkommen, Bildung und Arbeitszufriedenheit:

	Alter	Einkommen	Bildung	Arbeitszufriedenheit
Alter	1	0.5	0.3	0.2
Einkommen	0.5	1	0.8	0.6
Bildung	0.3	0.8	1	0.4
Arbeitszufriedenheit	0.2	0.8	0.4	1

In diesem Beispiel können wir sehen, dass Einkommen und Bildung eine starke positive Korrelation von 0,8 aufweisen. Das bedeutet, dass Menschen mit einem höheren Bildungsniveau tendenziell auch ein höheres Einkommen haben.

Alter und Einkommen weisen ebenfalls eine mäßig positive Korrelation von 0,5 auf, was darauf hindeutet, dass das Einkommen mit dem Alter steigt. Die Korrelation zwischen Alter und Arbeitszufriedenheit beträgt jedoch nur 0,2, was zeigt, dass das Alter kein starker Prädiktor für die Arbeitszufriedenheit ist.

Die Korrelationsmatrix ist eine nützliche Zusammenfassung oder Analyse, wie diese Variablen zueinander in Beziehung stehen.

Wie erstellt man eine Korrelationsmatrix in Excel?

Die Erstellung einer Korrelationsmatrix in Excel ist einfach und kann Ihnen helfen, die Beziehungen zwischen verschiedenen Variablen in Ihrem Datensatz zu analysieren.

Hier sehen Sie, wie Sie Schritt für Schritt vorgehen können:

1. Bereiten Sie Ihre Daten vor

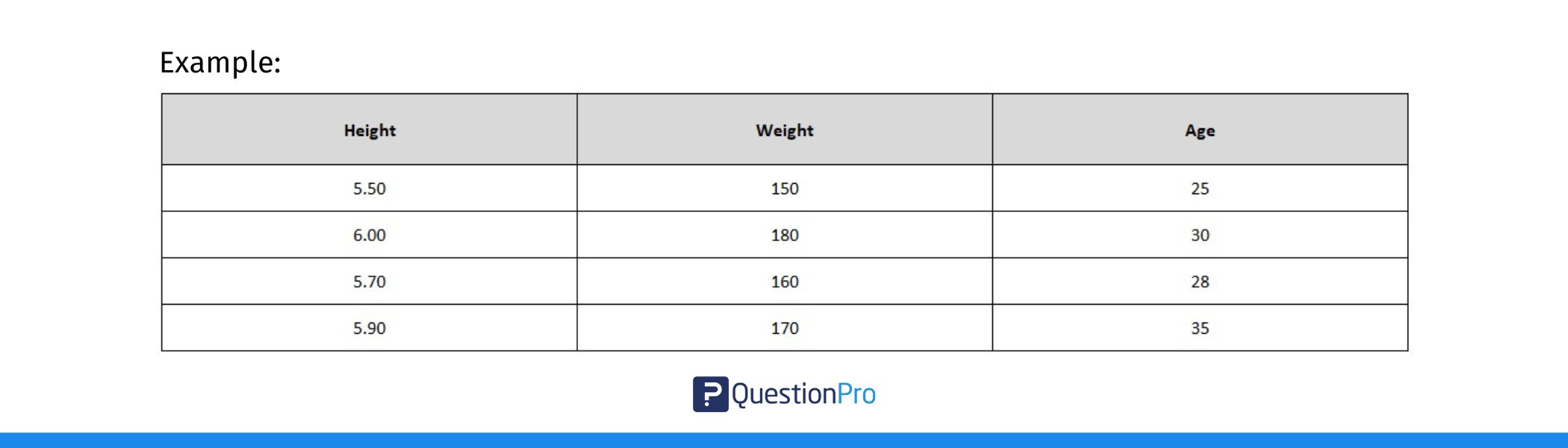
Stellen Sie zunächst sicher, dass Ihre Daten in Spalten organisiert sind. Jede Spalte sollte für eine andere Variable stehen, und die Zeilen sollten die Werte für jede Beobachtung enthalten.

Wenn Sie zum Beispiel die Beziehung zwischen Größe, Gewicht und Alter untersuchen, sollte jede dieser Variablen in einer eigenen Spalte stehen.

2. Wählen Sie die Daten:

Markieren Sie die Daten (ohne die Spaltenüberschriften), für die Sie die Korrelation berechnen möchten.

3. Verwenden Sie die Funktion CORREL:

Wenn Sie die Korrelation zwischen zwei Variablen manuell berechnen möchten:

• Klicken Sie auf eine leere Zelle, in der das Korrelationsergebnis erscheinen soll.
• Geben Sie =CORREL( ein und wählen Sie dann den Bereich für die erste Variable (z.B. Höhe).
• Wählen Sie nach dem Komma den Bereich für die zweite Variable (z.B. Gewicht).
  Wenn Sie beispielsweise das Verhältnis zwischen Größe und Gewicht analysieren, wählen Sie nach der Auswahl des Bereichs für die Größendaten den Bereich für die Gewichtsdaten in Ihrer Kalkulationstabelle aus.
• Drücken Sie die Eingabetaste, und Excel zeigt den Korrelationskoeffizienten zwischen diesen beiden Variablen an.

4. Erstellen Sie die vollständige Korrelationsmatrix:

Um eine vollständige Korrelationsmatrix zu erstellen, wiederholen Sie die obigen Schritte für jedes Paar von Variablen:

• Erstellen Sie in der ersten Zeile Überschriften für jede Variable (z.B. Größe, Gewicht, Alter).
• Listen Sie in der ersten Spalte die gleichen Variablen auf.
• Füllen Sie die Zellen aus, indem Sie die Korrelation zwischen jedem Variablenpaar mit =CORREL() berechnen.

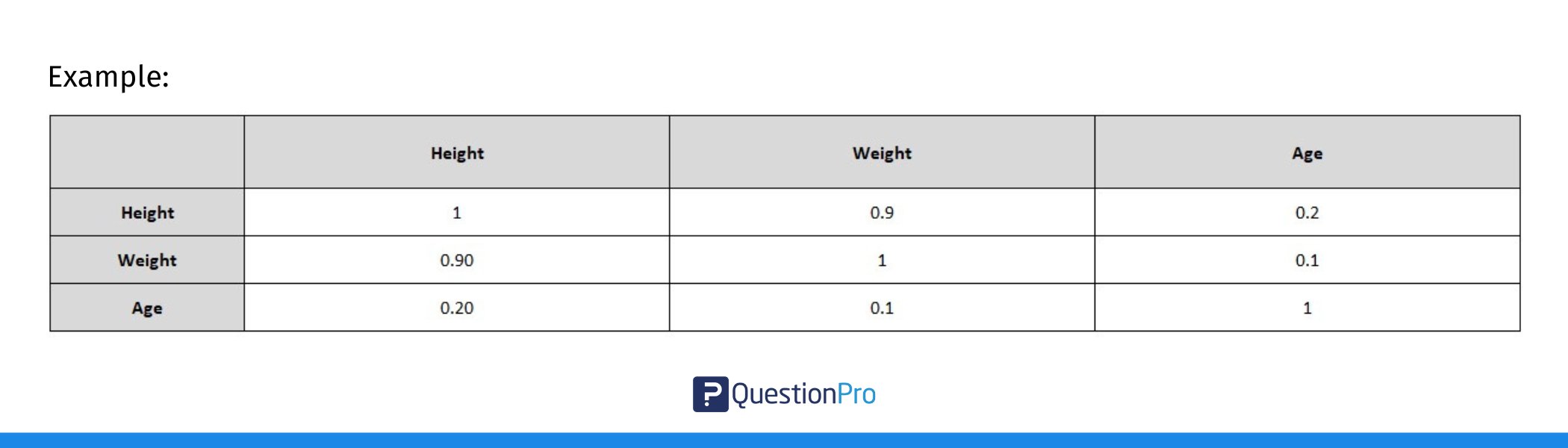
In dieser Tabelle:

• Die Diagonalwerte sind 1, da jede Variable mit sich selbst perfekt korreliert ist.
• Die Werte außerhalb der Diagonalen sind die Korrelationen zwischen Paaren von Variablen.

5. Verwenden Sie das Datenanalyse-Tool (optional):

Wenn Sie automatisch eine Korrelationsmatrix für alle Ihre Daten erstellen möchten, können Sie das integrierte Datenanalyse-Toolpaket von Excel verwenden:

• Gehen Sie auf die Registerkarte Daten im Menüband.
• Klicken Sie auf Datenanalyse (wenn Sie diese Option nicht sehen, müssen Sie möglicherweise das Analysis ToolPak in den Excel-Optionen aktivieren).
• Wählen Sie Korrelation aus der Liste und klicken Sie auf OK.
• Wählen Sie den Eingabebereich (Ihre Daten), markieren Sie das Feld Beschriftungen in der ersten Zeile (wenn Sie Kopfzeilen haben) und wählen Sie, wo die Ergebnisse angezeigt werden sollen.
• Klicken Sie auf OK, und Excel erstellt eine vollständige Korrelationsmatrix für Sie!

6. Interpretieren Sie die Ergebnisse:

Sobald die Matrix erstellt ist, sehen Sie sich die Korrelationswerte an:

• Werte in der Nähe von +1 bedeuten eine starke positive Beziehung.
• Werte in der Nähe von -1 bedeuten eine stark negative Beziehung.
• Werte nahe 0 deuten auf eine geringe bis gar keine Beziehung hin.

Und das war’s! Sie haben nun eine Korrelationsmatrix in Excel erstellt, mit der Sie analysieren können, wie die verschiedenen Variablen in Ihrem Datensatz miteinander in Beziehung stehen.

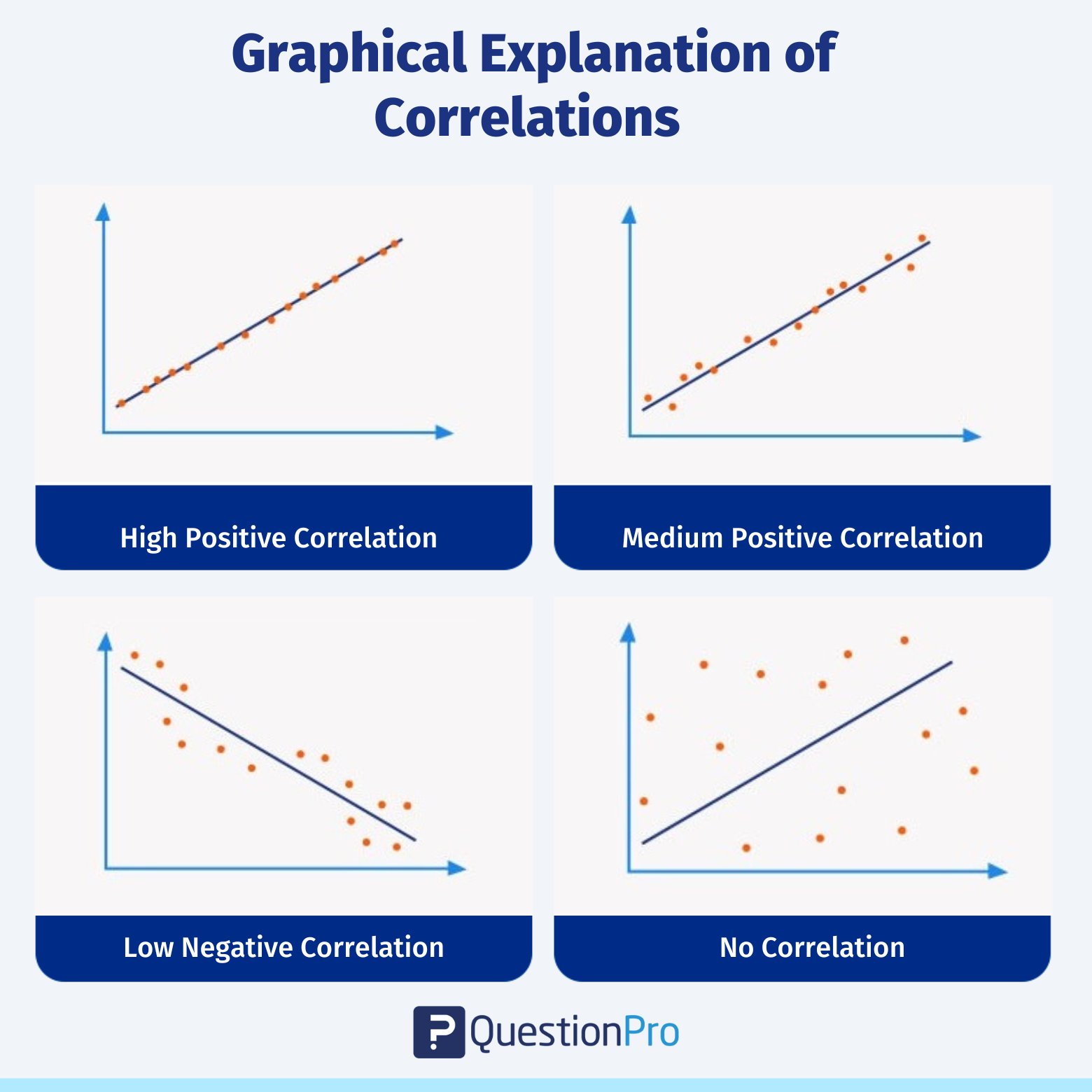
Arten von Korrelationskoeffizienten

Bei der Messung der Beziehung zwischen zwei Variablen gibt es verschiedene Methoden, die Sie je nach Art der Daten und der Beziehung zwischen den Variablen anwenden können.

Hier ein Blick auf einige der gängigsten Korrelationskoeffizienten:

1. Pearson-Korrelationskoeffizient (r)

Der Pearson-Korrelationskoeffizient ist die am häufigsten verwendete Methode zur Messung der linearen Beziehung zwischen zwei kontinuierlichen Variablen. Er funktioniert am besten, wenn die Daten normal verteilt sind und ist ideal für parametrische Daten. Um den Pearson-Korrelationskoeffizienten zu ermitteln, berechnen Sie die Kovarianz der beiden Variablen und dividieren sie durch das Produkt ihrer Standardabweichungen.

Dieser Koeffizient gibt einen Wert zwischen -1 und +1 an, wobei +1 für eine perfekte positive lineare Beziehung steht, -1 für eine perfekte negative lineare Beziehung und 0 bedeutet, dass es keine lineare Beziehung zwischen den Variablen gibt.

Spearman’s Rangkorrelationskoeffizient ‚ρ‘ (rho)

Der Spearmansche Rangkorrelationskoeffizient wird verwendet, wenn Ihre Daten ordinal sind (Rangdaten) oder wenn die Beziehung zwischen den Variablen zwar nicht linear, aber dennoch monoton ist (d. h., wenn eine Variable zunimmt, nimmt die andere tendenziell zu oder ab, aber nicht unbedingt in einer geraden Linie).

Um den Spearman’schen Rangkorrelationskoeffizienten zu ermitteln, ordnen Sie zunächst die Werte jeder Variablen vom niedrigsten zum höchsten Wert, berechnen die Differenz zwischen den Rängen für jedes Paar von Datenpunkten und verwenden diese Rangdifferenzen in der Spearman-Formel zur Berechnung der Korrelation.

Im Gegensatz zum Pearson-Koeffizienten wird bei der Spearman-Korrelation nicht davon ausgegangen, dass die Daten einer Normalverteilung folgen, was sie zu einer nicht-parametrischen Alternative macht.

3. Kendall’s Tau

Kendall’s Tau ist eine weitere nicht-parametrische Methode, die der Spearman’schen Rangkorrelation ähnelt. Sie ist besonders nützlich, wenn Sie mit kleineren Stichprobengrößen oder ordinalen Daten arbeiten. Wie die Spearman-Methode misst sie die Stärke einer monotonen Beziehung, aber sie verwendet einen etwas anderen Ansatz und liefert oft zuverlässigere Ergebnisse, wenn die Ränge gleich sind oder die Datensätze klein sind.

Der Korrelationskoeffizient fasst die Beziehung zusammen. Denken Sie jedoch daran, dass Korrelation nicht gleichbedeutend mit Kausalität ist, d. h.selbst wenn zwei Variablen hoch korreliert sind, bedeutet dies nicht, dass die eine die andere verursacht.

Wenn Sie ein tieferes Verständnis für die Berechnung und Interpretation des Pearson-Korrelationskoeffizienten haben möchten, empfehlen wir Ihnen unseren ausführlichen Leitfaden: Pearson Korrelationskoeffizient.

Korrelationsmatrix vs. Kovarianzmatrix

Wir wissen, dass eine Korrelationsmatrix eine Tabelle mit den Korrelationskoeffizienten zwischen mehreren Variablen ist. Sie stellt die Stärke und Richtung ihrer Beziehungen auf einer standardisierten Skala von -1 bis +1 dar. Eine Kovarianzmatrix hingegen ist eine Tabelle, die die Kovarianzen zwischen den Variablen aufzeigt. Sie misst, wie Veränderungen in einer Variable mit Veränderungen in einer anderen zusammenhängen, ohne jedoch die Werte zu standardisieren.

Obwohl sowohl die Kovarianzmatrix als auch die Korrelationsmatrix in der Statistik verwendet werden, um Muster zu untersuchen, sind sie unterschiedlich. Die erste zeigt, wie unterschiedlich zwei oder mehr Variablen voneinander sind, während die zweite zeigt, wie ähnlich sie sich sind.

Korrelations- und Kovarianzmatrizen unterscheiden sich unter anderem durch folgende Merkmale:

Basis	Korrelationsmatrix	Kovarianz-Matrix
Beziehung	Sie hilft dabei, sowohl die Richtung (positiv/negativ) als auch die Stärke (niedrig/mittel/hoch) der Beziehung zwischen zwei Variablen herauszufinden.	Sie misst nur, in welche Richtung die Beziehung zwischen zwei Variablen geht.
Angegebene Teilmenge und Bereich	Sie ist ein Teil der Kovarianz und hat einen Wertebereich zwischen 0 und 1 (-1 bis 1).	Es ist eine größere Idee, die keine klaren Grenzen hat (sie kann bis ins Unendliche gehen).
Dimension	Es kann nicht gemessen werden.	Sie kann gemessen werden.

Beschränkungen der Korrelation

Die Korrelation ist zwar ein leistungsfähiges Instrument, hat aber auch einige Einschränkungen, die man kennen sollte, um Fehlinterpretationen oder Missbrauch der Ergebnisse zu vermeiden.

Hier sind die wichtigsten Einschränkungen der Korrelation:

• Korrelation bedeutet nicht gleich Kausalität: Eine starke Korrelation bedeutet nicht, dass eine Variable die Veränderung der anderen verursacht.
• Empfindlich gegenüber Ausreißern: Extremwerte können die Korrelation verzerren und die Beziehung stärker oder schwächer erscheinen lassen, als sie ist.
• Misst nur lineare Beziehungen: Korrelationsmethoden wie Pearson konzentrieren sich nur auf lineare Beziehungen und können nicht-lineare Muster übersehen.
• Setzt Homoskedastizität voraus: Die Korrelation setzt voraus, dass die Varianz der Daten über alle Ebenen der Variablen hinweg konsistent ist.

Fazit

Eine Korrelationsmatrix ist ein nützliches Instrument, um herauszufinden, wie verschiedene Variablen miteinander in Beziehung stehen. Indem wir uns die Korrelationskoeffizienten zwischen zwei Variablen ansehen, erfahren wir, wie sie zusammenhängen und wie sich Änderungen in einer Variable auf die anderen Variablen auswirken können.

QuestionPro verfügt über eine Vielzahl von Funktionen und Tools, die Ihnen bei der Analyse und Erstellung einer Korrelationsmatrix helfen können. Die Umfrageplattform hilft Ihnen, Daten von den Befragten zu sammeln, und die Analysetools helfen Ihnen, eine Korrelationsmatrix aus den gesammelten Daten zu erstellen. QuestionPro verfügt außerdem über fortschrittliche Analysetools, mit denen Sie Verbindungen zwischen Variablen finden und Multikollinearität erkennen können.

QuestionPro ist ein nützliches Tool für Forscher und Analysten, die herausfinden möchten, wie verschiedene Variablen miteinander in Beziehung stehen und was man aus Umfragedaten lernen kann.

MEHR LERNEN KOSTENLOSES PROBLEM

Häufig gestellte Fragen (FAQs)