
Die Korrelation ist ein grundlegendes Konzept in der Statistik und Datenanalyse, das hilft, die Beziehung zwischen zwei Variablen zu verstehen. Während starke positive oder negative Korrelationen oft hervorgehoben werden, ist eine Nullkorrelation ebenso wichtig.
Das bedeutet, dass es keine lineare Beziehung zwischen den Variablen gibt. Mit anderen Worten: Änderungen in einer Variable sagen keine Änderungen in der anderen voraus.
In diesem Blog werden wir uns mit dem Konzept der Nullkorrelation befassen und eine klare Definition, anschauliche Beispiele und Methoden zu ihrer Ermittlung liefern.
Was ist eine Nullkorrelation?
Nullkorrelation ist ein statistischer Begriff, der eine Situation beschreibt, in der es keine lineare Beziehung zwischen zwei Variablen gibt. Wenn zwei Variablen eine Nullkorrelation aufweisen, sagen Änderungen in einer Variable keine Änderungen in der anderen Variable voraus. Der Korrelationskoeffizient, der den Grad und die Richtung der Beziehung zwischen den Variablen misst, ist in diesem Fall genau Null.
Das Verständnis dieser Korrelation ist in der statistischen Analyse wichtig, da es hilft, Variablen zu identifizieren, die nicht in einer prädiktiven Beziehung zueinander stehen, was für die Erstellung statistischer Modelle oder die Interpretation von Datenmustern entscheidend ist.
Warum ist Nullkorrelation wichtig?
Die Nullkorrelation ist aus mehreren Gründen ein wichtiges Konzept in der Statistik und Datenanalyse:
Es identifiziert Unabhängigkeit
Sie hilft dabei, Variablen zu identifizieren, die linear unabhängig voneinander sind. Wenn zwei Variablen eine Nullkorrelation aufweisen, geben Änderungen in einer Variable keine Auskunft über Änderungen in der anderen. Dies ist entscheidend für das Verständnis der Struktur der Daten und der Beziehungen (oder deren Fehlen) zwischen den Variablen.
Es verbessert die statistischen Modelle
Bei der Regressionsanalyse und anderen statistischen Modellen kann die Einbeziehung von Variablen mit dieser Korrelation zur abhängigen Variable Rauschen hinzufügen und die Vorhersagekraft des Modells verringern. Durch die Identifizierung und den Ausschluss solcher Variablen können die Modelle vereinfacht und effizienter gestaltet werden, was zu einer besseren Leistung und Interpretierbarkeit führt.
Diese Korrelation hilft, Fehlinterpretationen zu vermeiden
Das Verständnis dieser Korrelation verhindert eine Fehlinterpretation der Daten.
- Zum Beispiel könnte ein Forscher aufgrund seiner Intuition oder seiner ersten Beobachtungen fälschlicherweise auf eine Beziehung zwischen zwei Variablen schließen.
Die Berechnung des Korrelationskoeffizienten und die Feststellung, dass er gleich Null ist, verdeutlicht, dass keine lineare Beziehung besteht und vermeidet falsche Schlussfolgerungen.
Es hebt nicht-lineare Beziehungen hervor
Es verdeutlicht die Möglichkeit von nicht-linearen Beziehungen. Wenn zwei Variablen eine Nullkorrelation aufweisen, bedeutet das nicht unbedingt, dass sie nicht miteinander in Beziehung stehen; sie könnten eine komplexe, nicht lineare Beziehung haben. Wenn Sie dies erkennen, können Sie weitere Untersuchungen mit anderen Methoden durchführen, wie z.B. nicht-lineare Regression oder Datentransformationen.
Korrelation hilft bei der Versuchsplanung
Bei der Versuchsplanung kann das Wissen, welche Variablen eine Nullkorrelation aufweisen, bei der Auswahl der Variablen helfen, die einbezogen oder kontrolliert werden sollen. Dies hilft bei der Planung robusterer Experimente, bei denen der Einfluss irrelevanter Variablen minimiert wird, was zu klareren, zuverlässigeren Ergebnissen führt.
Es versteht variables Verhalten
Sie bietet Einblicke in das Verhalten von Variablen in einem Datensatz. In der Finanzanalyse kann das Wissen darüber, welche Vermögenswerte eine Nullkorrelation zueinander aufweisen, bei der Portfoliodiversifizierung helfen, da die Kombination solcher Vermögenswerte das Gesamtrisiko verringern kann.
Es unterstützt das Testen von Hypothesen
Bei Hypothesentests ist diese Korrelation oft eine Nullhypothese.
- Wenn Sie beispielsweise testen, ob zwei Variablen miteinander verbunden sind, könnte die Nullhypothese besagen, dass die Korrelation zwischen ihnen gleich Null ist.
Die Feststellung, ob dies wahr oder falsch ist, hilft dabei, Hypothesen zu bestätigen oder zu widerlegen.
Was sind die Beispiele für Nullkorrelation?
Beispiele für diese Korrelation, bei der Veränderungen in einer Variable nicht mit Veränderungen in einer anderen Variable übereinstimmen, finden sich in verschiedenen Bereichen, wie z.B.:
Bereich der Forschung
Beispiel: Anzahl der wissenschaftlichen Veröffentlichungen und Lieblings-Eiscreme-Geschmack
Eine Studie untersucht den Zusammenhang zwischen der Anzahl der wissenschaftlichen Veröffentlichungen eines Forschers und seiner Lieblingseissorte.
Es gibt keinen logischen Zusammenhang zwischen der Anzahl der wissenschaftlichen Arbeiten, die ein Forscher veröffentlicht, und seiner Vorliebe für einen bestimmten Eisgeschmack. Folglich wird erwartet, dass diese beiden Variablen diese Korrelation aufweisen.
Bereich Bildung
Beispiel: Die Schuhgröße der Schüler und ihre Noten in Mathematik
In einer Bildungsstudie wird untersucht, ob es einen Zusammenhang zwischen den Schuhgrößen von Schülern und ihren Noten in Mathematik gibt.
Die Schuhgröße ist ein physisches Merkmal, das keinen Einfluss auf die akademischen Leistungen eines Schülers in Mathematik hat. Daher ist die Korrelation zwischen Schuhgröße und Mathenoten wahrscheinlich gleich Null.
Bereich der Gesundheitsfürsorge
Beispiel: Blutgruppe und Auftreten von Erkältungen
Eine Studie im Gesundheitswesen untersucht, ob es einen Zusammenhang zwischen der Blutgruppe eines Menschen und der Anzahl der Erkältungen gibt, die er in einem Jahr bekommt.
Die Blutgruppe steht nicht im Zusammenhang mit der Häufigkeit von Erkältungskrankheiten, die von verschiedenen anderen Faktoren wie der Exposition gegenüber Viren und der Stärke des Immunsystems beeinflusst wird. Daher wird erwartet, dass der Zusammenhang zwischen der Blutgruppe und der Häufigkeit von Erkältungskrankheiten gleich Null ist.
Wie erkennt man eine Nullkorrelation?
Hier werden wir untersuchen, wie Sie diese Korrelation durch visuelle Inspektion, statistische Berechnungen, Hypothesentests und kontextbezogene Analysen identifizieren können.
1. Visuelle Inspektion anhand von Streudiagrammen
Streudiagramme sind ein effektives Instrument zur visuellen Beurteilung der Beziehung zwischen zwei Variablen.
Erstellen Sie ein Streudiagramm:
- Setzen Sie eine Variable auf die x-Achse und die andere auf die y-Achse.
- Suchen Sie nach einem erkennbaren Trend oder Muster in den Datenpunkten.
Erkennen von Korrelationen:
- Wenn die Punkte wahllos verstreut sind und keinen klaren Trend aufweisen (weder nach oben noch nach unten), deutet dies auf eine Korrelation hin.
- Eine zufällige Streuung bedeutet, dass keine Linie (egal ob gerade oder gekrümmt) gut zu den Datenpunkten passen kann.
Beispiel:
- Schuhgrößen der Schüler im Vergleich zu den Mathenoten: Wenn Sie die Schuhgrößen gegen die Mathenoten auftragen und eine zufällige Streuung von Punkten ohne Trend sehen, deutet dies auf eine Nullkorrelation hin.
2. Berechnen Sie den Korrelationskoeffizienten
Der Pearson-Korrelationskoeffizient (r) ist das gängigste Maß für die lineare Korrelation.
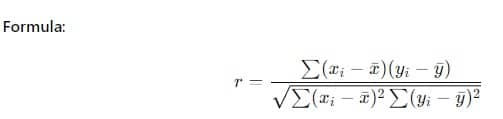
Schritte:
- Sammeln Sie gepaarte Datenpunkte für die beiden Variablen.
- Ermitteln Sie den Mittelwert (Durchschnitt) der einzelnen Variablen.
- Berechnen Sie, wie weit jeder Datenpunkt vom Mittelwert entfernt ist.
- Multiplizieren Sie die Abweichungen für jedes Paar und addieren Sie die Produkte.
- Verwenden Sie die Formel, um den Korrelationskoeffizienten zu ermitteln.
Korrelation interpretieren:
Wert nahe bei 0: Wenn 𝑟 r nahe bei 0 liegt, deutet dies auf eine geringe bis keine lineare Beziehung zwischen den Variablen hin.
Beispiel:
- Schuhgrößen und Mathe-Noten: Wenn das berechnete 𝑟 ungefähr 0 ist, bestätigt dies eine Nullkorrelation.
3. Testen Sie die Hypothese
Mit statistischen Hypothesentests kann festgestellt werden, ob ein beobachteter Korrelationskoeffizient signifikant von Null verschieden ist.
Schritte:
- Null-Hypothese: Nehmen Sie an, dass der Korrelationskoeffizient Null ist.
- Alternative Hypothese: Nehmen Sie an, dass der Korrelationskoeffizient nicht Null ist.
- Berechnen Sie die Teststatistik: Verwenden Sie einen t-Test für den Korrelationskoeffizienten.
- Bestimmen Sie den p-Wert: Vergleichen Sie den p-Wert mit einem Signifikanzniveau (z.B. 0,05).
Nullkorrelation:
- Wenn der p-Wert größer als das Signifikanzniveau ist, lehnen Sie die Nullhypothese nicht ab, was bedeutet, dass die Korrelation nicht signifikant von Null verschieden ist.
Beispiel:
- Blutgruppe und Inzidenz von Erkältungen: Testen Sie die Korrelation zwischen der Blutgruppe und dem Auftreten von Erkältungen. Wenn der p-Wert hoch ist, bedeutet dies, dass die beobachtete Korrelation statistisch nicht signifikant ist und somit eine Nullkorrelation vorliegt.
4. Kontextuelle Analyse verstehen
Um Korrelationsergebnisse zu interpretieren, ist es wichtig, den Kontext und den theoretischen Hintergrund der Variablen zu verstehen.
Schritte:
- Untersuchen Sie die Variablen: Betrachten Sie die Art und die erwarteten Beziehungen zwischen den Variablen.
- Domänenwissen anwenden: Nutzen Sie Wissen aus dem Bereich, um Hypothesen darüber aufzustellen, ob eine Beziehung zu erwarten ist.
Nullkorrelation:
- Wenn Theorie und frühere Forschungen keinen logischen Zusammenhang vermuten lassen, unterstützt dies die Feststellung dieser Korrelation.
Beispiel:
- Blutgruppe und Erkältungshäufigkeit: Das Wissen, dass die Blutgruppe keinen Einfluss auf die Anfälligkeit für Erkältungen hat, unterstützt die Interpretation, dass es keine Korrelation gibt, falls eine solche gefunden wird.
Negative vs. positive Korrelation vs. Nullkorrelation
Die Korrelation ist ein statistisches Maß, das die Stärke und Richtung der Beziehung zwischen zwei Variablen beschreibt. Hier finden Sie eine detaillierte Erklärung der negativen, positiven und Nullkorrelation:
Positive Korrelation
- Definition: Eine positive Korrelation liegt vor, wenn sich zwei Variablen in dieselbe Richtung bewegen. Wenn eine Variable zunimmt, nimmt auch die andere Variable zu, und wenn die eine abnimmt, nimmt auch die andere ab.
- Beispiel: Die Beziehung zwischen Größe und Gewicht. Im Allgemeinen nimmt mit der Körpergröße einer Person auch ihr Gewicht tendenziell zu.
- Grafische Darstellung: In einem Streudiagramm neigen die Punkte dazu, sich um eine Linie zu gruppieren, die von links nach rechts ansteigt.
Negative Korrelation
- Definition: Eine negative Korrelation liegt vor, wenn sich zwei Variablen in entgegengesetzte Richtungen bewegen. Wenn eine Variable zunimmt, nimmt die andere Variable ab und umgekehrt.
- Beispiel: Die Beziehung zwischen der Zeit, die für das Lernen aufgewendet wird, und der Anzahl der Fehler, die bei einem Test gemacht werden. Im Allgemeinen sinkt die Anzahl der Fehler, je mehr Zeit mit Lernen verbracht wird.
- Grafische Darstellung: In einem Streudiagramm neigen die Punkte dazu, sich um eine Linie zu gruppieren, die von links nach rechts abfällt.
Nullkorrelation
- Definition: Es zeigt an, dass es keine Beziehung zwischen den beiden Variablen gibt. Änderungen in einer Variable sagen keine Änderungen in der anderen Variable voraus.
- Beispiel: Die Beziehung zwischen der Schuhgröße einer Person und ihrem Intelligenzquotienten (IQ). Es gibt keine logische Verbindung zwischen diesen beiden Variablen.
- Grafische Darstellung: In einem Streudiagramm sind die Punkte zufällig verteilt, ohne dass ein Muster oder eine Neigung erkennbar ist.
Wie kann QuestionPro bei der Korrelationsanalyse helfen?
QuestionPro, eine robuste Umfrageplattform, bietet umfassende Tools zur effektiven Durchführung von Korrelationsanalysen. Hier erfahren Sie, wie QuestionPro Ihnen bei der Durchführung von Korrelationsanalysen helfen kann:
Mühelose Datenerfassung
QuestionPro vereinfacht den Prozess der Datenerfassung durch seine benutzerfreundlichen Tools zur Erstellung von Umfragen. Sie können Umfragen entwerfen und verteilen, um quantitative Daten zu verschiedenen Variablen von Interesse zu erfassen. Die Plattform unterstützt verschiedene Fragetypen, so dass Sie detaillierte und relevante Daten effizient erfassen können.
Automatisierte Datenanalyse
Sobald die Daten gesammelt sind, bietet QuestionPro integrierte Analysetools für die Korrelationsanalyse. Sie können ganz einfach Korrelationen berechnen, die die Stärke und Richtung der linearen Beziehung zwischen zwei Variablen messen. Der lineare Korrelationskoeffizient reicht von -1 bis 1, wobei:
- 1 bedeutet eine perfekte positive Korrelation.
- -1 bedeutet eine perfekte negative Korrelation.
- 0 bedeutet keine Korrelation.
Visuelle Darstellung
QuestionPro bietet Visualisierungstools, die Ihnen bei der Interpretation der Ergebnisse Ihrer Korrelationsanalyse helfen. Es können Streudiagramme und Korrelationsmatrizen erstellt werden, um die Beziehungen zwischen den Variablen grafisch darzustellen. Diese visuelle Hilfe ist wichtig, um Trends und Muster schnell zu erkennen.
Erkennen von Mustern und Trends
Mit der Korrelationsanalyse von QuestionPro haben die Forscher die Korrelation (positiv, negativ oder null) zwischen den Variablen beobachtet:
- Positive Korrelation: Beide Variablen bewegen sich in dieselbe Richtung. Zum Beispiel können höhere Werbeausgaben mit höheren Umsätzen korrelieren.
- Negative Korrelation: Die Variablen tendieren dazu, sich in entgegengesetzte Richtungen zu bewegen. Zum Beispiel könnte eine erhöhte Bildschirmzeit mit einer geringeren akademischen Leistung korrelieren.
- Nullkorrelation: Es besteht keine Beziehung zwischen den Variablen. Zum Beispiel korreliert die Anzahl der Schuljahre nicht mit der Anzahl der Buchstaben im Namen einer Person.
Praktische Anwendungen
Die Korrelationsanalyse in QuestionPro kann für verschiedene praktische Anwendungen genutzt werden, wie z.B.:
- Marktforschung: Messen Sie die Effektivität von Marketingkampagnen, indem Sie die Werbeausgaben mit der Verkaufsleistung in Beziehung setzen.
- Gesundheitswesen: Beurteilen Sie den Zusammenhang zwischen der Einnahme von Medikamenten und den Ergebnissen für den Patienten, wie z.B. den Blutdruckwerten.
- Bildung: Bestimmen Sie den Einfluss der Lerngewohnheiten auf die akademische Leistung, indem Sie die Lernstunden mit den Noten korrelieren.
Fazit
Eine Nullkorrelation zwischen zwei Variablen bedeutet, dass es keine lineare Beziehung gibt. Das bedeutet, dass Änderungen in einer Variablen nicht mit Änderungen in einer anderen korrespondieren. Durch die Berechnung von Korrelationskoeffizienten und die Visualisierung von Daten durch Streudiagramme können Forscher genau feststellen, ob Variablen korreliert, positiv korreliert, negativ korreliert sind oder diese Korrelation aufweisen.
Die Verwendung von QuestionPro für die Korrelationsanalyse in Ihren Umfragen bietet eine leistungsstarke Möglichkeit, sinnvolle Beziehungen zwischen Variablen aufzudecken. Mit der intuitiven Benutzeroberfläche von QuestionPro, den fortschrittlichen Analysetools und den umfassenden Berichtsfunktionen können Sie Korrelationsanalysen effizient durchführen und wertvolle Erkenntnisse aus Ihren Daten ableiten. Kontaktieren Sie QuestionPro noch heute für weitere Informationen!






