Die Regressionsanalyse ist vielleicht eine der am häufigsten verwendeten statistischen Methoden zur Untersuchung oder Schätzung der Beziehung zwischen einer Reihe von unabhängigen und abhängigen Variablen. Bei der statistischen Analyse ist die Unterscheidung zwischen kategorischen Daten und numerischen Daten von wesentlicher Bedeutung, da kategorische Daten eindeutige Kategorien oder Bezeichnungen beinhalten, während numerische Daten aus messbaren Größen bestehen.
Sie wird auch als Sammelbegriff für verschiedene Datenanalysetechniken verwendet, die in einer qualitativen Forschungsmethode zur Modellierung und Analyse zahlreicher Variablen eingesetzt werden. Bei der Regressionsmethode ist die abhängige Variable ein Prädiktor oder ein erklärendes Element, und die abhängige Variable ist das Ergebnis oder eine Antwort auf eine bestimmte Frage.
LERNEN SIE ÜBER: Statistische Analysemethoden
Definition der Regressionsanalyse
Die Regressionsanalyse wird häufig zur Modellierung oder Analyse von Daten verwendet. Die meisten Umfrageanalysten verwenden sie, um die Beziehung zwischen den Variablen zu verstehen, die dann zur Vorhersage des genauen Ergebnisses genutzt werden können.
Beispiel: Angenommen, ein Unternehmen, das Erfrischungsgetränke herstellt, möchte seine Produktionsstätte an einen neuen Standort verlegen. Bevor es loslegt, möchte das Unternehmen sein Umsatzmodell und die verschiedenen Faktoren, die sich darauf auswirken könnten, analysieren. Daher führt das Unternehmen eine Online-Umfrage mit einem speziellen Fragebogen durch.
Nach der Verwendung der Regressionsanalyse wird es für das Unternehmen einfacher, die Umfrageergebnisse zu analysieren und die Beziehung zwischen verschiedenen Variablen wie Strom und Umsatz zu verstehen – hier ist der Umsatz die abhängige Variable.
LERNEN ÜBER: Ebene der Analyse
Darüber hinaus hilft das Verständnis der Beziehung zwischen verschiedenen unabhängigen Variablen wie der Preisgestaltung, der Anzahl der Mitarbeiter und der Logistik mit dem Umsatz dem Unternehmen, die Auswirkungen der verschiedenen Faktoren auf Umsatz und Gewinn abzuschätzen.
Umfrageforscher verwenden diese Technik häufig, um eine Korrelation zwischen verschiedenen Variablen von Interesse zu untersuchen und zu finden. Sie bietet die Möglichkeit, den Einfluss verschiedener unabhängiger Variablen auf eine abhängige Variable zu messen.
Insgesamt erspart die Regressionsanalyse den Forschern zusätzlichen Aufwand, mehrere unabhängige Variablen in Tabellen anzuordnen und ihre Wirkung auf eine abhängige Variable zu testen oder zu berechnen. Verschiedene Arten von analytischen Forschungsmethoden werden häufig eingesetzt, um neue Geschäftsideen zu bewerten und fundierte Entscheidungen zu treffen.
Ein kostenloses Konto erstellen
Arten der Regressionsanalyse
Forscher lernen in der Regel zuerst die lineare und die logistische Regression. Aufgrund der weiten Verbreitung dieser beiden Methoden und ihrer einfachen Anwendung denken viele Analysten, dass es nur zwei Arten von Modellen gibt. Jedes Modell hat seine eigenen Besonderheiten und Fähigkeiten, wenn bestimmte Bedingungen erfüllt sind.
In diesem Blog werden die sieben gebräuchlichen Methoden der multiplen Regressionsanalyse erläutert, die zur Interpretation der ausgezählten Daten in verschiedenen Formaten verwendet werden können.
01. Lineare Regressionsanalyse
Sie ist eine der bekanntesten Modellierungstechniken, da sie zu den ersten Elite-Methoden der Regressionsanalyse gehört, die von den Menschen beim Erlernen der prädiktiven Modellierung aufgegriffen wurde. Hier ist die abhängige Variable kontinuierlich, und die unabhängige Variable ist häufiger kontinuierlich oder diskret mit einer linearen Regressionslinie.
Bitte beachten Sie, dass es bei der multiplen linearen Regression mehr als eine unabhängige Variable gibt als bei der einfachen linearen Regression. Daher sollte die lineare Regression nur dann verwendet werden, wenn eine lineare Beziehung zwischen der unabhängigen und der abhängigen Variable besteht.
Beispiel
Ein Unternehmen kann die lineare Regression nutzen, um die Wirksamkeit von Marketingkampagnen, Preisgestaltung und Werbeaktionen auf den Absatz eines Produkts zu messen. Nehmen wir an, ein Unternehmen, das Sportartikel verkauft, möchte herausfinden, ob die Mittel, die es in das Marketing und das Branding seiner Produkte investiert hat, sich gelohnt haben oder nicht.
Die lineare Regression ist die beste statistische Methode zur Interpretation der Ergebnisse. Das Beste an der linearen Regression ist, dass sie auch dabei hilft, die undurchsichtigen Auswirkungen der einzelnen Marketing- und Branding-Aktivitäten zu analysieren und gleichzeitig das Potenzial der einzelnen Komponenten zur Regulierung der Verkäufe zu kontrollieren.
Wenn das Unternehmen zwei oder mehr Werbekampagnen gleichzeitig durchführt, eine im Fernsehen und zwei im Radio, dann kann die lineare Regression leicht den unabhängigen und kombinierten Einfluss der gemeinsamen Durchführung dieser Werbung analysieren.
LERNEN SIE ÜBER: Datenanalyse-Projekte
02. Logistische Regressionsanalyse
Die logistische Regression wird häufig verwendet, um die Wahrscheinlichkeit des Erfolgs oder Misserfolgs eines Ereignisses zu bestimmen. Die logistische Regression wird immer dann verwendet, wenn die abhängige Variable binär ist, wie 0/1, Wahr/Falsch oder Ja/Nein. Man kann also sagen, dass die logistische Regression dazu verwendet wird, entweder die geschlossenen Fragen in einer Umfrage oder die Fragen, die numerische Antworten in einer Umfrage erfordern, zu analysieren.
Bitte beachten Sie, dass die logistische Regression nicht wie die lineare Regression eine lineare Beziehung zwischen einer abhängigen und einer unabhängigen Variable voraussetzt. Die logistische Regression wendet eine nicht-lineare logarithmische Transformation zur Vorhersage des Quotenverhältnisses an. Daher kann sie problemlos mit verschiedenen Arten von Beziehungen zwischen einer abhängigen und einer unabhängigen Variable umgehen.
Beispiel
Die logistische Regression wird häufig zur Analyse kategorischer Daten verwendet, insbesondere für binäre Antwortdaten bei der Modellierung von Geschäftsdaten. Häufiger wird die logistische Regression verwendet, wenn die abhängige Variable kategorisch ist, z.B. um vorherzusagen, ob die von einer Person gemachten Gesundheitsangaben echt(1) oder betrügerisch sind, um zu verstehen, ob der Tumor bösartig ist(1) oder nicht.
Unternehmen nutzen die logistische Regression, um vorherzusagen, ob die Verbraucher einer bestimmten Bevölkerungsgruppe ihr Produkt kaufen oder bei der Konkurrenz einkaufen werden, und zwar auf der Grundlage von Alter, Einkommen, Geschlecht, Ethnie, Wohnsitz, früherem Kauf usw.
03. Polynomiale Regressionsanalyse
Die polynomiale Regression wird in der Regel zur Analyse krummliniger Daten verwendet, wenn die Potenz einer unabhängigen Variable größer als 1 ist. Bei dieser Regressionsanalysemethode ist die Best-Fit-Linie nie eine „gerade Linie“, sondern immer eine „Kurvenlinie“, die in die Datenpunkte passt.
Bitte beachten Sie, dass die polynomiale Regression besser geeignet ist, wenn zwei oder mehr Variablen Exponenten haben und einige nicht.
Darüber hinaus kann es nicht-linear trennbare Daten modellieren und bietet die Freiheit, den genauen Exponenten für jede Variable zu wählen, und das bei voller Kontrolle über die verfügbaren Modellierungsfunktionen.
Beispiel
In Kombination mit der Response Surface Analysis gilt die polynomiale Regression als eine der ausgefeilten statistischen Methoden, die häufig in der Multisource-Feedbackforschung eingesetzt werden. Die polynomiale Regression wird vor allem in der Finanz- und Versicherungsbranche verwendet, wo die Beziehung zwischen abhängigen und unabhängigen Variablen krummlinig ist.
Angenommen, eine Person möchte ihre Ausgaben planen, indem sie ermittelt, wie lange sie braucht, um eine bestimmte Summe zu verdienen. Die polynomiale Regression kann unter Berücksichtigung des Einkommens und der voraussichtlichen Ausgaben leicht die genaue Zeit bestimmen, die er/sie arbeiten muss, um diesen bestimmten Betrag zu verdienen.
04. Schrittweise Regressionsanalyse
Dabei handelt es sich um einen halbautomatischen Prozess, bei dem ein statistisches Modell entweder durch Hinzufügen oder Entfernen der abhängigen Variable auf Basis der t-Statistiken ihrer geschätzten Koeffizienten erstellt wird.
Wenn Sie die schrittweise Regression richtig anwenden, haben Sie mehr Daten zur Verfügung als mit jeder anderen Methode. Sie funktioniert gut, wenn Sie mit einer großen Anzahl von unabhängigen Variablen arbeiten. Sie nimmt lediglich eine Feinabstimmung des Modells der Analyseeinheit vor, indem sie die Variablen nach dem Zufallsprinzip ansteuert.
Die schrittweise Regressionsanalyse wird empfohlen, wenn es mehrere unabhängige Variablen gibt, wobei die Auswahl der unabhängigen Variablen automatisch ohne menschliches Eingreifen erfolgt.
Bitte beachten Sie, dass bei der schrittweisen Regressionsmodellierung die Variable zu der Gruppe der erklärenden Variablen hinzugefügt oder von ihr abgezogen wird. Die Menge der hinzugefügten oder entfernten Variablen wird in Abhängigkeit von der Teststatistik des geschätzten Koeffizienten ausgewählt.
Beispiel
Nehmen wir an, Sie haben eine Reihe unabhängiger Variablen wie Alter, Gewicht, Körperoberfläche, Dauer des Bluthochdrucks, Basalpuls und Stressindex, anhand derer Sie deren Einfluss auf den Blutdruck analysieren möchten.
Bei der schrittweisen Regression wird automatisch die beste Teilmenge der unabhängigen Variablen ausgewählt. Dabei wird entweder zunächst keine Variable ausgewählt, um dann weiterzugehen (indem eine Variable nach der anderen hinzugefügt wird), oder es wird mit allen Variablen im Modell begonnen und dann rückwärts vorgegangen (indem eine Variable nach der anderen entfernt wird).
Mithilfe der Regressionsanalyse können Sie also die Auswirkungen jeder einzelnen oder einer Gruppe von Variablen auf den Blutdruck berechnen.
05. Ridge-Regressionsanalyse
Die Ridge-Regression basiert auf einer gewöhnlichen Methode der kleinsten Quadrate, die zur Analyse von Daten mit Multikollinearität (Daten, bei denen die unabhängigen Variablen stark korreliert sind) verwendet wird. Kollinearität kann als eine nahezu lineare Beziehung zwischen Variablen erklärt werden.
Wenn Multikollinearität vorliegt, sind die Schätzungen der kleinsten Quadrate unverzerrt, aber wenn die Differenz zwischen ihnen größer ist, dann kann sie weit vom wahren Wert entfernt sein. Bei der Ridge-Regression werden die Standardfehler jedoch eliminiert, indem den Regressionsschätzungen ein gewisser Grad an Verzerrung hinzugefügt wird, um zuverlässigere Schätzungen zu erhalten.
Wenn Sie möchten, können Sie sich auch in unserem Blog über Selection Bias informieren.
Bitte beachten Sie, dass die durch die Ridge-Regression abgeleiteten Annahmen denen der kleinsten quadratischen Regression ähneln, der einzige Unterschied ist die Normalität. Obwohl der Wert des Koeffizienten bei der Ridge-Regression eingeschränkt ist, erreicht er nie den Wert Null, was darauf hindeutet, dass die Variablen nicht ausgewählt werden können.
Beispiel
Angenommen, Sie sind begeistert von zwei Gitarristen, die auf einer Veranstaltung in Ihrer Nähe auftreten, und Sie gehen hin, um sich ihren Auftritt anzusehen, um herauszufinden, wer der bessere Gitarrist ist. Doch als der Auftritt beginnt, stellen Sie fest, dass beide gleichzeitig schwarze und blaue Noten spielen.
Ist es möglich, den besten Gitarristen herauszufinden, der den größten Einfluss auf den Klang hat, wenn beide laut und schnell spielen? Da beide Gitarristen unterschiedliche Noten spielen, ist es wesentlich schwieriger, sie zu unterscheiden. Dies ist der beste Fall von Multikollinearität, die die Standardfehler der Koeffizienten tendenziell erhöht.
Die Ridge-Regression befasst sich mit der Multikollinearität in solchen Fällen und beinhaltet eine Verzerrungs- oder Schrumpfungsschätzung, um die Ergebnisse abzuleiten.
06. Lasso-Regressionsanalyse
Lasso (Least Absolute Shrinkage and Selection Operator) ähnelt der Ridge-Regression, verwendet jedoch eine absolute Verzerrung anstelle der quadratischen Verzerrung, die bei der Ridge-Regression verwendet wird.
Sie wurde bereits 1989 als Alternative zur traditionellen Kleinste-Quadrate-Schätzung entwickelt, um die meisten Probleme im Zusammenhang mit der Überanpassung bei Daten mit einer großen Anzahl unabhängiger Variablen zu lösen.
Lasso kann beides – die Auswahl von Variablen und deren Regularisierung zusammen mit einem weichen Schwellenwert – durchführen. Die Anwendung der Lasso-Regression erleichtert die Ableitung einer Teilmenge von Prädiktoren, die den Vorhersagefehler bei der Analyse einer quantitativen Antwort minimieren.
Bitte beachten Sie, dass Regressionskoeffizienten, die nach der Schrumpfung den Wert Null erreichen, aus dem Lasso-Modell ausgeschlossen werden. Im Gegenteil, Regressionskoeffizienten mit einem Wert von mehr als Null sind stark mit den Antwortvariablen assoziiert, wobei die erklärenden Variablen entweder quantitativ, kategorial oder beides sein können.
Beispiel
Angenommen, ein Automobilunternehmen möchte eine Forschungsanalyse zum durchschnittlichen Kraftstoffverbrauch von Autos in den USA durchführen. Als Stichproben wählten sie 32 Automodelle und 10 Merkmale des Automobildesigns – Anzahl der Zylinder, Hubraum, Bruttopferdestärken, Hinterachsübersetzung, Gewicht, ¼-Meile-Zeit, vs. Motor, Getriebe, Anzahl der Gänge und Anzahl der Vergaser.
Wie Sie sehen können, ist eine Korrelation zwischen der Antwortvariablen mpg (miles per gallon) und einigen Variablen wie Gewicht, Hubraum, Anzahl der Zylinder und Pferdestärken extrem korreliert. Das Problem kann mit dem glmnet-Paket in R und der Lasso-Regression für die Merkmalsauswahl analysiert werden.
07. Elastisches Netz – Regressionsanalyse
Es ist eine Mischung aus Ridge- und Lasso-Regressionsmodellen, die mit L1- und L2-Normen trainiert wurden. Das elastische Netz bewirkt einen Gruppierungseffekt, bei dem stark korrelierte Prädiktoren dazu neigen, gemeinsam in das Modell hinein- bzw. aus ihm herauszufallen. Die Verwendung des Regressionsmodells mit elastischem Netz wird empfohlen, wenn die Anzahl der Prädiktoren weitaus größer ist als die Anzahl der Beobachtungen.
Bitte beachten Sie, dass das Modell der elastischen Netzregression als Alternative zum Lasso-Regressionsmodell entstanden ist, da der Variablenbereich des Lassos zu stark von den Daten abhängig war, was es instabil machte. Durch die Verwendung der elastischen Netzregression waren die Statistiker in der Lage, die Nachteile der Ridge- und Lassoregression zu überbrücken, um das Beste aus beiden Modellen herauszuholen.
Beispiel
Ein klinisches Forschungsteam, das Zugang zu einem Microarray-Datensatz über Leukämie (LEU) hatte, war daran interessiert, eine diagnostische Regel auf der Grundlage des Expressionsniveaus der vorgelegten Genproben zu erstellen, um die Art der Leukämie vorherzusagen. Der Datensatz, den sie hatten, bestand aus einer großen Anzahl von Genen und wenigen Proben.
Außerdem erhielten sie einen bestimmten Satz von Proben, die als Trainingsproben verwendet werden sollten, von denen einige mit Leukämie Typ 1 (akute lymphatische Leukämie) und einige mit Leukämie Typ 2 (akute myeloische Leukämie) infiziert waren.
Die Modellanpassung und die Auswahl der Tuning-Parameter durch zehnfachen CV wurden mit den Trainingsdaten durchgeführt. Dann verglichen sie die Leistung dieser Methoden, indem sie den mittleren quadratischen Fehler der Vorhersage anhand der Testdaten berechneten, um die erforderlichen Ergebnisse zu erhalten.
Anwendung der Regressionsanalyse in der Marktforschung
Eine Marktforschungsumfrage konzentriert sich auf drei Hauptmatrizen: Kundenzufriedenheit, Kundentreue und Kundenbefürwortung. Denken Sie daran, dass diese Matrizen zwar etwas über den Zustand und die Absichten der Kunden aussagen, aber nicht darüber, wie man die Lage verbessern kann. Daher ist ein detaillierter Fragebogen, mit dem die Verbraucher nach den Gründen für ihre Unzufriedenheit befragt werden, definitiv ein Weg, um praktische Erkenntnisse zu gewinnen.
Es hat sich jedoch gezeigt, dass es den Menschen oft schwer fällt, ihre Motivation oder Demotivation darzulegen oder ihre Zufriedenheit oder Unzufriedenheit zu beschreiben. Außerdem messen die Menschen einigen rationalen Faktoren wie dem Preis, der Verpackung usw. immer eine übermäßige Bedeutung bei. Insgesamt fungiert es als prädiktives Analyse- und Prognoseinstrument in der Marktforschung.
Wenn sie als Prognoseinstrument eingesetzt wird, kann die Regressionsanalyse die Verkaufszahlen eines Unternehmens bestimmen, indem sie externe Marktdaten mit einbezieht. Ein multinationales Unternehmen führt eine Marktforschungsstudie durch, um die Auswirkungen verschiedener Faktoren wie BIP (Bruttoinlandsprodukt), CPI (Verbraucherpreisindex) und anderer ähnlicher Faktoren auf sein Umsatzmodell zu verstehen.
Offensichtlich wurde die Regressionsanalyse unter Berücksichtigung der prognostizierten Marketing-Indikatoren verwendet, um einen vorläufigen Umsatz vorherzusagen, der in zukünftigen Quartalen und sogar in zukünftigen Jahren erzielt werden wird. Je weiter Sie jedoch in die Zukunft gehen, desto unzuverlässiger werden die Daten und desto größer wird die Fehlerspanne.
Fallstudie zur Anwendung der Regressionsanalyse
Ein Unternehmen, das Wasseraufbereitungsanlagen herstellt, wollte die Faktoren verstehen, die zur Beliebtheit der Marke führen. Die Umfrage war das beste Medium, um bestehende und potenzielle Kunden zu erreichen. Es wurde eine groß angelegte Verbraucherumfrage geplant und ein diskreter Fragebogen mit dem besten Umfragetool erstellt.
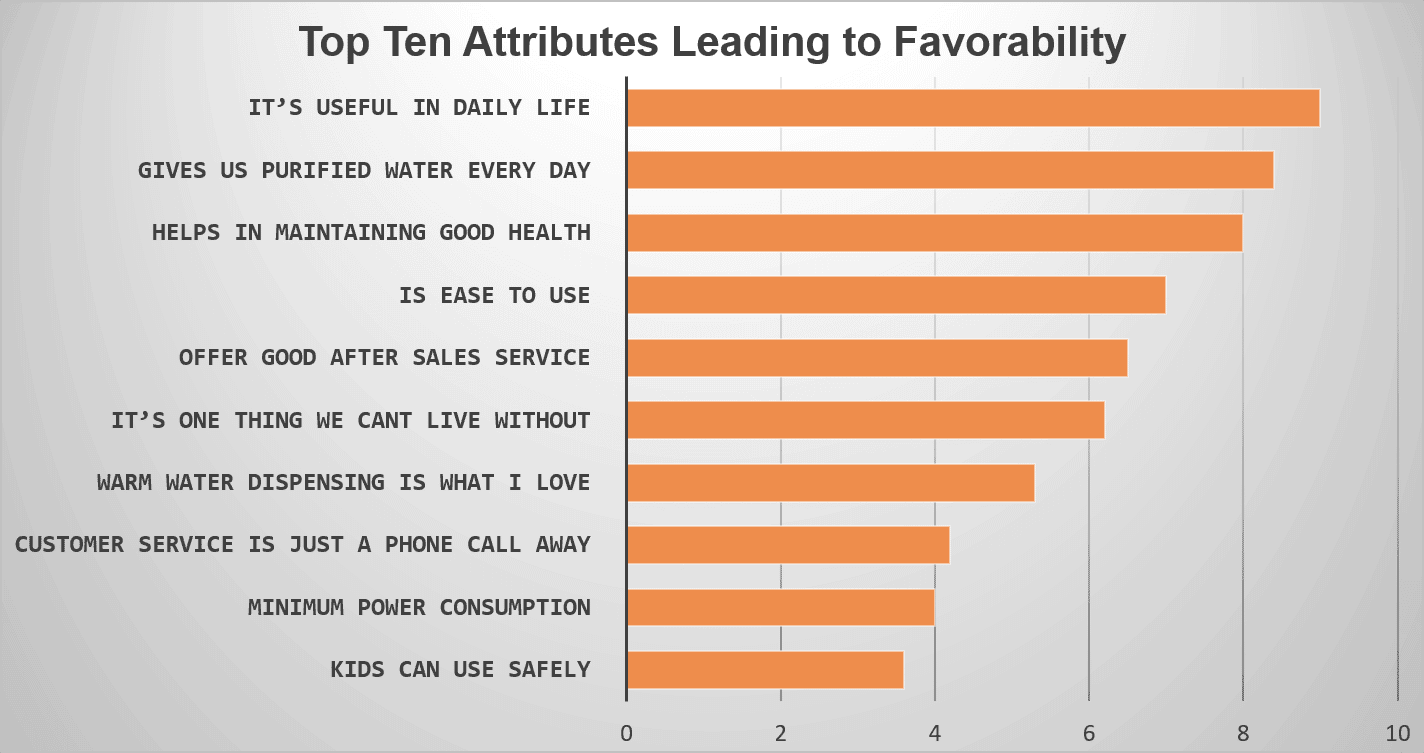
In der Umfrage wurde eine Reihe von Fragen zur Marke, zur Beliebtheit, zur Zufriedenheit und zur wahrscheinlichen Unzufriedenheit gestellt. Nachdem wir optimale Antworten auf die Umfrage erhalten hatten, wurde eine Regressionsanalyse durchgeführt, um die zehn wichtigsten Faktoren, die für die Markengunst verantwortlich sind, einzugrenzen.
Alle zehn abgeleiteten Attribute (die in der Abbildung unten aufgeführt sind) haben auf die eine oder andere Weise ihre Bedeutung für die Beliebtheit der jeweiligen Wasseraufbereitungsmarke unterstrichen.
Wie gewinnt die Regressionsanalyse Erkenntnisse aus Umfragen?
Es ist einfach, eine Regressionsanalyse mit Excel oder SPSS durchzuführen, aber dabei muss man die Bedeutung von vier Zahlen für die Interpretation der Daten verstehen.
Die ersten beiden Zahlen der vier Zahlen beziehen sich direkt auf das Regressionsmodell selbst.
- F-Wert: Er hilft bei der Messung der statistischen Signifikanz des Umfragemodells. Denken Sie daran, dass ein F-Wert von deutlich weniger als 0,05 als aussagekräftiger angesehen wird. Ein F-Wert von weniger als 0,05 stellt sicher, dass das Ergebnis der Umfrageanalyse nicht zufällig ist.
- R-Quadrat: Dies ist der Wert, bei dem die unabhängigen Variablen versuchen, den Umfang der Bewegung der abhängigen Variablen zu erklären. Wenn der R-Quadrat-Wert 0,7 beträgt, kann eine getestete unabhängige Variable 70 % der Bewegung der abhängigen Variable erklären. Das bedeutet, dass die Ergebnisse der Umfrageanalyse, die wir erhalten, in hohem Maße vorhersagend sind und als genau angesehen werden können.
Die beiden anderen Zahlen beziehen sich auf jede der unabhängigen Variablen bei der Interpretation der Regressionsanalyse.
- P-Wert: Wie der F-Wert ist auch der P-Wert statistisch signifikant. Außerdem gibt er an, wie relevant und statistisch signifikant der Effekt der unabhängigen Variable ist. Auch hier suchen wir nach einem Wert von weniger als 0,05.
- Interpretation: Die vierte Zahl bezieht sich auf den Koeffizienten, der sich nach der Messung der Auswirkungen der Variablen ergibt. Wir testen zum Beispiel mehrere unabhängige Variablen, um einen Koeffizienten zu erhalten. Er sagt uns, „um welchen Wert die abhängige Variable voraussichtlich steigen wird, wenn die unabhängigen Variablen (die wir berücksichtigen) um eins steigen, während alle anderen unabhängigen Variablen auf demselben Wert stagnieren.
In einigen wenigen Fällen wird der einfache Koeffizient durch einen standardisierten Koeffizienten ersetzt, der den Beitrag der einzelnen unabhängigen Variablen zur Veränderung der abhängigen Variable zeigt.
Ein kostenloses Konto erstellen
Vorteile der Verwendung der Regressionsanalyse in einer Online-Umfrage
01. Erhalten Sie Zugang zu prädiktiver Analytik
Wussten Sie, dass der Einsatz einer Regressionsanalyse zum Verständnis der Ergebnisse einer Unternehmensumfrage die Möglichkeit bietet, zukünftige Chancen und Risiken aufzudecken?
Wenn wir zum Beispiel einen bestimmten Werbeplatz im Fernsehen gesehen haben, können wir die genaue Anzahl der Unternehmen vorhersagen, die diese Daten nutzen, um ein Höchstgebot für diesen Platz zu schätzen. Die Finanz- und Versicherungsbranche als Ganzes ist sehr auf die Regressionsanalyse von Umfragedaten angewiesen, um Trends und Möglichkeiten für eine genauere Planung und Entscheidungsfindung zu erkennen.
02. Verbessern Sie die operative Effizienz
Wussten Sie, dass Unternehmen die Regressionsanalyse nutzen, um ihre Geschäftsprozesse zu optimieren?
So führen Unternehmen beispielsweise vor der Einführung einer neuen Produktlinie Verbraucherumfragen durch, um die Auswirkungen verschiedener Faktoren auf die Produktion, die Verpackung, den Vertrieb und den Konsum des Produkts besser zu verstehen.
Eine datengestützte Vorausschau hilft, Vermutungen, Hypothesen und interne Politik aus der Entscheidungsfindung zu entfernen. Ein tieferes Verständnis der Bereiche, die sich auf die betriebliche Effizienz und den Umsatz auswirken, führt zu einer besseren Geschäftsoptimierung.
03. Quantitative Unterstützung bei der Entscheidungsfindung
Unternehmensumfragen generieren heute eine Vielzahl von Daten zu Finanzen, Umsatz, Betrieb, Einkäufen usw., und Unternehmer sind in hohem Maße auf verschiedene Datenanalysemodelle angewiesen, um fundierte Geschäftsentscheidungen zu treffen.
Die Regressionsanalyse hilft Unternehmen beispielsweise dabei, fundierte strategische Personalentscheidungen zu treffen. Die Durchführung und Interpretation der Ergebnisse von Mitarbeiterbefragungen wie Umfragen zum Mitarbeiterengagement, Umfragen zur Mitarbeiterzufriedenheit, Umfragen zur Verbesserung des Arbeitgebers, Umfragen zum Ausscheiden von Mitarbeitern usw. verbessert das Verständnis der Beziehung zwischen Mitarbeitern und Unternehmen.
Es hilft auch dabei, sich einen Überblick über bestimmte Probleme zu verschaffen, die sich auf die Arbeitskultur, das Arbeitsumfeld und die Produktivität des Unternehmens auswirken. Darüber hinaus reduzieren intelligente, geschäftsorientierte Interpretationen den riesigen Haufen von Rohdaten in verwertbare Informationen, um eine fundiertere Entscheidung zu treffen.
04. Vermeiden Sie Fehler aufgrund von Intuitionen
Wenn man weiß, wie man die Regressionsanalyse für die Interpretation von Umfrageergebnissen einsetzt, kann man dem Management leicht faktische Unterstützung bieten, um fundierte Entscheidungen zu treffen; aber wissen Sie, dass sie auch dabei hilft, Fehler in der Beurteilung zu vermeiden?
Ein Einkaufszentrum-Manager glaubt zum Beispiel, wenn er die Schließzeit des Einkaufszentrums verlängert, dann wird dies zu mehr Umsatz führen. Die Regressionsanalyse widerspricht der Annahme, dass die Vorhersage höherer Einnahmen aufgrund gestiegener Umsätze die erhöhten Betriebskosten, die durch längere Arbeitszeiten entstehen, nicht stützen wird.
Fazit
Die Regressionsanalyse ist eine nützliche statistische Methode zur Modellierung und zum Verständnis der Beziehungen zwischen Variablen. Sie bietet zahlreiche Vorteile für verschiedene Datentypen und Interaktionen. Forscher und Analysten können nützliche Erkenntnisse über die Faktoren gewinnen, die eine abhängige Variable beeinflussen, und die Ergebnisse nutzen, um fundierte Entscheidungen zu treffen.
Mit QuestionPro Research können Sie die Effizienz und Genauigkeit der Regressionsanalyse verbessern, indem Sie die Prozesse der Datenerfassung, Analyse und Berichterstellung rationalisieren. Die benutzerfreundliche Oberfläche und die zahlreichen Funktionen der Plattform machen sie zu einem wertvollen Werkzeug für Forscher und Analysten, die Regressionsanalysen im Rahmen ihrer Forschungsprojekte durchführen.
Melden Sie sich noch heute für die kostenlose Testversion an und lassen Sie Ihre Forschungsträume fliegen!







