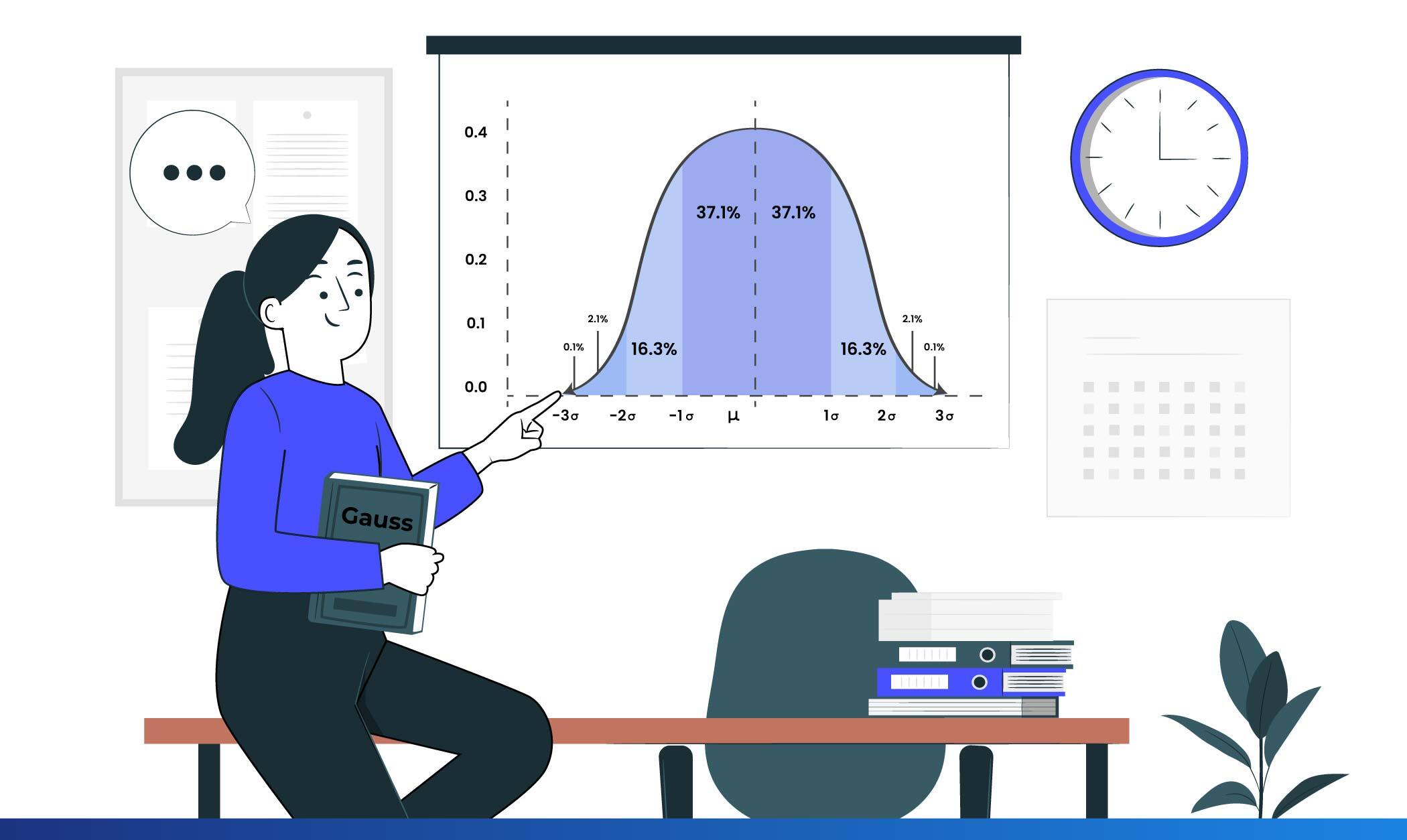
La campana de Gauss, también conocida como la Distribución Normal, lleva el nombre del matemático alemán Carl Friedrich Gauss, y se ha convertido en un pilar esencial en el análisis estadístico y se usa en diversas disciplinas.
En este artículo, exploramos la campana de Gauss desde su definición hasta sus aplicaciones prácticas, destacando sus ventajas y características distintivas.
¿Qué es una campana de Gauss?
La campana de Gauss, o distribución normal, es una función matemática que describe la forma en que se distribuyen los datos en un conjunto. Se caracteriza por su forma simétrica y la famosa apariencia de campana, con la mayoría de los datos concentrados alrededor de la media y dispersándose de manera uniforme hacia ambos lados. La función se define por dos parámetros principales: la media, que representa el centro de la distribución, y la desviación estándar, que mide la dispersión de los datos.
Su forma simétrica implica que la mitad de los datos se encuentran a la izquierda de la media y la otra mitad a la derecha. Además, alrededor del 68% de los datos se encuentran dentro de una desviación estándar de la media, mientras que el 95% se sitúa dentro de dos desviaciones estándar.
Otra característica interesante es que, independientemente de la forma de la distribución original, cuando se acumulan suficientes datos, la distribución tiende a seguir una forma de campana de Gauss. Este fenómeno es conocido como el Teorema del límite central, que subraya la omnipresencia de esta distribución en el análisis estadístico.
Ventajas de la campana de Gauss: ¿Por qué es tan poderosa?
La popularidad de la campana de Gauss radica en varias ventajas clave. En primer lugar, es altamente intuitiva y fácil de entender, lo que la convierte en una herramienta accesible incluso para aquellos que no tienen un fondo matemático extenso. Además, su amplia aplicabilidad permite modelar una amplia gama de situaciones del mundo real con precisión.
Otra ventaja fundamental es su capacidad para resumir la información en dos parámetros: la media y la desviación estándar. Esto simplifica enormemente el análisis y la interpretación de los datos, permitiendo a los investigadores y analistas obtener información valiosa de manera eficiente.
El Teorema del Límite Central establece que, dado un tamaño de muestra suficientemente grande, la distribución de la media de las muestras se aproxima a una distribución normal, independientemente de la forma de la distribución original. Esto hace que la campana de Gauss sea una herramienta poderosa para el análisis de grandes conjuntos de datos.
La campana de Gauss es fundamental en muchas pruebas estadísticas, como la prueba t de Student y la prueba de chi-cuadrado. Estas pruebas se basan en supuestos de normalidad para realizar inferencias sobre poblaciones.
Usos de la campana de Gauss
La campana de Gauss se aplica en una amplia variedad de campos, desde la física y la biología hasta la economía y la psicología. En estadística, es comúnmente utilizada para modelar fenómenos naturales, como la altura de una población o las puntuaciones en un examen. Además, esta distribución se utiliza como base para otras herramientas estadísticas y modelos más complejos.
La campana de Gauss, o distribución normal, se utiliza en una amplia variedad de campos debido a su versatilidad y capacidad para modelar numerosos fenómenos. Algunos de los usos más comunes incluyen:
Estadística descriptiva:
La campana de Gauss es fundamental para describir la distribución de datos en una población. Se utiliza para resumir y entender la tendencia central y la dispersión de un conjunto de datos.
Inferencia estadística:
En inferencia estadística, la campana de Gauss es crucial para realizar predicciones y estimaciones. Permite calcular intervalos de confianza y realizar pruebas de hipótesis, proporcionando herramientas fundamentales para la toma de decisiones basada en datos.
Investigación psicológica:
En psicología, la campana de Gauss se utiliza para modelar diversos fenómenos, como la distribución de coeficientes de inteligencia (CI) en una población. Además, es empleada en estudios de comportamiento y análisis de resultados de pruebas psicométricas.
Economía y finanzas:
En el ámbito económico y financiero, la campana de Gauss se utiliza para modelar la variabilidad de los rendimientos de activos financieros. El modelo de rendimientos logarítmicos sigue una distribución normal en muchos casos, lo que facilita la evaluación de riesgos y la toma de decisiones en inversiones.
Biología y medicina:
En biología, la distribución normal se encuentra en fenómenos como la altura de una población o la distribución de peso en una especie. En medicina, se aplica para analizar datos biométricos y evaluar la eficacia de tratamientos, entre otros usos.
Control de calidad:
La campana de Gauss se utiliza en el control de calidad para evaluar la consistencia y la variabilidad en la producción de bienes y servicios. Permite establecer límites de tolerancia y detectar posibles desviaciones en los procesos de fabricación.
Modelado de fenómenos naturales:
En diversas disciplinas científicas, como la física, la meteorología y la geología, la campana de Gauss se utiliza para modelar la distribución de variables, como la velocidad del viento, la temperatura o la concentración de sustancias químicas en un área determinada.
Machine learning y ciencia de datos:
En el campo del machine learning, la campana de Gauss es utilizada como suposición inicial en muchos algoritmos y modelos. Además, es común asumir que los errores de predicción siguen una distribución normal, lo que facilita el desarrollo y la interpretación de modelos.
Conoce más de la ciencia de datos
Ejemplo de campana de Gauss: Evaluación de rendimiento académico
Imaginemos que estamos analizando el rendimiento académico de los estudiantes en una escuela secundaria. Queremos comprender cómo se distribuyen las calificaciones en un examen de matemáticas y utilizar la campana de Gauss para obtener información valiosa sobre el desempeño general de la clase.
Paso 1: Recopilación de datos
Obtenemos las calificaciones de todos los estudiantes en el examen de matemáticas. Supongamos que hemos recopilado las siguientes calificaciones en una escala de 0 a 100:
78, 82, 85, 88, 90, 92, 94, 96, 98, 100
Paso 2: Cálculo de la media y desviación estándar
Calculamos la media y la desviación estándar de estas calificaciones. Supongamos que la media es 90 y la desviación estándar es 6. Estos valores son simplemente para ilustrar el ejemplo; en un escenario real, se calcularían a partir de los datos reales.
Paso 3: Creación de la campana de Gauss
Con la media y la desviación estándar, podemos crear la campana de Gauss que describe la distribución de las calificaciones. La mayoría de los estudiantes se concentran alrededor de la media, y la forma de campana refleja la probabilidad de obtener diferentes calificaciones.
Paso 4: Interpretación de la campana de Gauss
- 68% de los estudiantes: Alrededor del 68% de los estudiantes obtendrán calificaciones dentro de una desviación estándar de la media, es decir, entre 84 y 96.
- 95% de los estudiantes: Cerca del 95% de los estudiantes tendrán calificaciones dentro de dos desviaciones estándar de la media, en el rango de 78 a 102.
- 99.7% de los estudiantes: Prácticamente todos los estudiantes (99.7%) obtendrán calificaciones dentro de tres desviaciones estándar de la media, entre 72 y 108.
Paso 5: Toma de decisiones y evaluación de desempeño
Con esta distribución, los educadores pueden tomar decisiones informadas sobre la efectividad del examen y la enseñanza. Por ejemplo, si un gran número de estudiantes obtuvo calificaciones por debajo de la media, podría indicar áreas de mejora en la enseñanza. Además, la campana de Gauss proporciona una comprensión clara de cómo se distribuyen las calificaciones, lo que puede ayudar a establecer estándares de rendimiento y políticas educativas.
En este caso de uso, la campana de Gauss no sólo proporciona un resumen visual de la distribución de calificaciones, sino que también ofrece herramientas valiosas para la toma de decisiones educativas basadas en datos estadísticos. Este ejemplo ilustra cómo la distribución normal puede ser una poderosa herramienta en la evaluación y mejora continua del rendimiento académico.
Conclusión
En conclusión, la campana de Gauss es más que una simple curva matemática; es una herramienta esencial que ha demostrado su utilidad en una variedad de disciplinas. Su simplicidad, versatilidad y capacidad para resumir datos complejos en parámetros clave la convierten en un componente fundamental del análisis estadístico. A medida que continuamos explorando y comprendiendo el mundo que nos rodea, la campana de Gauss seguirá desempeñando un papel crucial en nuestra capacidad para modelar y entender los fenómenos con precisión y claridad.
Si buscas herramientas para recopilar datos de calidad para tus próximos proyectos, recuerda que en QuestionPro te podemos ayudar. Comienza creando una cuenta gratis de nuestro software para encuestas y descubre todo su potencial.



