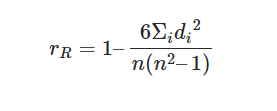El coeficiente de correlación de Spearman es una medida no paramétrica de la correlación de rango (dependencia estadística del ranking entre dos variables). Se utiliza principalmente para el análisis de datos.
Mide la fuerza y la dirección de la asociación entre dos variables clasificadas. Pero antes de hablar de la correlación de Spearman, es importante entender la correlación de Pearson, la cual es una medida estadística de la fuerza de una relación lineal entre datos emparejados.
Te recomiendo leer este artículo sobre las diferencias entre las pruebas no paramétricas y las pruebas paramétricas.
Para el cálculo y la prueba de significación de la variable de ranking, se requiere que la siguientes suposiciones de datos sean ciertas:
- Nivel de intervalo o ratio
- Relación lineal
- Bivariante distribuido
Si tus datos no cumplen con las suposiciones anteriores, necesitarás el coeficiente de correlación de Spearman. Para esto, es necesario saber qué función monótona es para entenderlo.
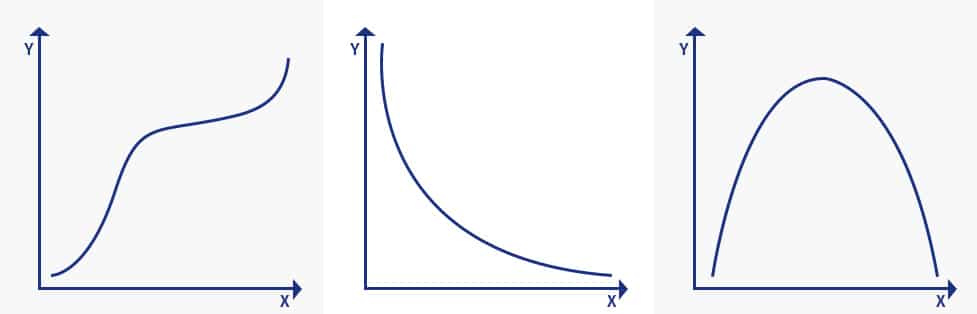
Una función monótona es aquella que nunca disminuye o nunca aumenta, ya que es un incremento variable independiente. Puede ser explicada usando la imagen de abajo:
La imagen explica tres conceptos de la función monótona:
- Monotónicamente en aumento: Cuando la variable “x” aumenta y la variable “y” nunca disminuye.
- Disminuye monótonamente: Cuando la variable “x” aumenta pero la variable “y” nunca aumenta.
- No monótono: Cuando la variable “x” aumenta y la variable “y” a veces aumenta y a veces disminuye.
La relación monótona es menos restrictiva cuando se compara con una relación lineal que se utiliza en el coeficiente de correlación de Pearson. Aunque la monotonicidad no es el último requisito, no será significativo perseguirla sin determinar realmente la fuerza y dirección de una relación monótona si ya se sabía que la relación entre la variable no es monótona.
Quizá te interese conocer cómo realizar un análisis de tabla cruzada.
Cómo calcular el coeficiente de correlación de Spearman
n= número de puntos de datos de las dos variables
di= diferencia de rango del elemento «n”
El Coeficiente Spearman,⍴, puede tomar un valor entre +1 y -1 donde,
- Un valor de +1 en ⍴ significa una perfecta asociación de rango
- Un valor 0 en ⍴ significa que no hay asociación de rangos
- Un valor de -1 en ⍴ significa una perfecta asociación negativa entre los rangos.
Si el valor de ⍴ se acerca a 0, la asociación entre los dos rangos es más débil.
Debemos ser capaces de clasificar los datos antes de proceder con el coeficiente de correlación de Spearman. Es importante observar que si se incrementa una variable, la otra sigue una relación monótona.
Descubre cómo analizar los datos de una investigación con el siguiente artículo.
Cómo se usa el coeficiente de correlación de Spearman
En cada nivel, deberás comparar los valores de las dos variables. Aquí tenemos un ejemplo de cómo funcionan los cálculos:
Los resultados de 9 estudiantes en Historia y Geografía se mencionan en la siguiente tabla.
Paso 1: Crear una tabla con los datos obtenidos.
Paso 2: Comienza por clasificar los dos conjuntos de datos. La clasificación de los datos puede lograrse asignando la clasificación «1» al número más grande de la columna, «2» al segundo número más grande, y así sucesivamente. El valor más pequeño generalmente obtendrá la clasificación más baja. Esto debe hacerse para ambos conjuntos de mediciones.
Paso 3: Agrega una tercera columna “d” a tu conjunto de datos, “d” aquí denota la diferencia entre los rangos. Por ejemplo, si el rango de física del primer estudiante es 3 y el rango de matemáticas es 5, entonces la diferencia en el rango es 3. En la cuarta columna, cuadrar sus valores “d”.
Paso 4: Sumar todos los valores del cuadrado “d” que es 12 (∑d cuadrada).
Paso 5: Insertar estos valores en la fórmula.
=1-(6*12)/(9(81-1))
=1-72/720
=1-01
=0.9
El coeficiente de correlación de Spearman para estos datos es de 0.9 y como se mencionó anteriormente si el valor de ⍴ se acerca a +1 entonces tienen una asociación perfecta de rango.
Cómo llevar a cabo el coeficiente de correlación de Spearman con QuestionPro
En esta sección, aprenderás a ejecutar el coeficiente de correlación de Spearman en tu encuesta online.
Paso 1: Ve a Mis Encuestas →Selecciona la encuesta→Análisis
Paso 2: Haz clic en Análisis de correlación
Paso 3: Haz clic en el botón Generar Coeficiente de Spearman para obtener un informe detallado.
En el ejemplo anterior, el coeficiente de correlación de Spearman se utiliza para averiguar la relación entre las dos variables, la experiencia laboral e ingresos mensuales. Una idea general es que los ingresos mensuales deben aumentar con la experiencia laboral, lo que significa que debe haber una asociación positiva entre las dos variables, lo que se demuestra por el valor de rs que es de 0,97.
Si quieres hacer uso de esta u otras funciones de nuestra plataforma para algún proyecto de investigación, no dudes en contactar a alguno de nuestros expertos.
Por último, quizá te interese leer el siguiente artículo que habla sobre la investigación correlacional.