
La correlación es un concepto fundamental en estadística y análisis de datos, que ayuda a entender la relación entre dos variables. Aunque las correlaciones fuertes, positivas o negativas, suelen destacarse, la correlación nula o cero es igualmente importante.
Significa que no hay una relación lineal entre las variables. En otras palabras, los cambios en una variable no predicen cambios en la otra.
En este artículo, exploraremos el concepto de correlación nula, proporcionando una definición clara, ejemplos ilustrativos y métodos para determinarla.
¿Qué es una correlación nula o cero?
La correlación nula es un término estadístico que describe una situación en la que no hay una relación lineal entre dos variables. Cuando dos variables tienen una correlación cero, los cambios en una variable no predicen cambios en la otra. El coeficiente de correlación, que mide el grado y la dirección de la relación entre variables, es exactamente cero en este caso.
Comprender esta correlación es importante en el análisis estadístico porque ayuda a identificar variables que no tienen una relación predictiva entre sí, lo cual es crucial al construir modelos estadísticos o interpretar patrones de datos.
Conoce más de los tipos de correlación.
¿Por qué es importante la correlación cero?
La correlación nula o cero es un concepto importante en estadística y análisis de datos por varias razones, tales como:
Identifica la independencia
Ayuda a identificar variables que son linealmente independientes entre sí. Si dos variables tienen una correlación cero, los cambios en una variable no proporcionan ninguna información sobre los cambios en la otra. Esto es crucial para entender la estructura de los datos y las relaciones (o la falta de ellas) entre variables.
Mejora los modelos estadísticos
En el análisis de regresión y otros modelos estadísticos, incluir variables con esta correlación en la variable dependiente puede añadir ruido y reducir el poder predictivo del modelo. Al identificar y excluir tales variables, los modelos pueden simplificarse y hacerse más eficientes, lo que conduce a un mejor rendimiento y facilidad de interpretación.
Evita la mala interpretación
Comprender esta correlación previene la mala interpretación de los datos.
Por ejemplo, un investigador podría inferir erróneamente una relación entre dos variables basándose en la intuición o en observaciones iniciales. Calcular el coeficiente de correlación y encontrar que es cero aclara que no existe una relación lineal, evitando conclusiones falsas.
Destaca las relaciones no lineales
Destaca la posibilidad de relaciones no lineales. Si dos variables tienen una correlación nula, no necesariamente significa que no estén relacionadas; podrían tener una relación compleja, no lineal. Reconocer esto puede impulsar una mayor investigación utilizando otros métodos, como la regresión no lineal o transformaciones de datos.
Guía el diseño experimental
En el diseño experimental, conocer qué variables tienen una correlación cero puede guiar la selección de variables para incluir o controlar. Esto ayuda a diseñar experimentos más robustos donde se minimiza la influencia de variables irrelevantes, llevando a resultados más claros y confiables.
Comprender el comportamiento de las variables
Proporciona información sobre el comportamiento de las variables en un conjunto de datos. En el análisis financiero, entender qué activos tienen una correlación cero entre sí puede ayudar en la diversificación de la cartera, ya que combinar tales activos puede reducir el riesgo general.
Apoya la prueba de hipótesis
En la prueba de hipótesis, esta correlación es a menudo una hipótesis nula.
Por ejemplo, al probar si dos variables están relacionadas, la hipótesis nula podría afirmar que la correlación entre ellas es cero. Establecer si esto es verdadero o falso ayuda a validar o refutar hipótesis.
¿Cuáles son los ejemplos de correlación cero?
Ejemplos de esta correlación, donde los cambios en una variable no corresponden con cambios en otra variable, se pueden encontrar en varios campos como:
Campo de investigación
Ejemplo: Número de publicaciones científicas y sabor de helado favorito
Un estudio investiga la relación entre el número de publicaciones científicas de un investigador y su sabor de helado favorito.
No hay una conexión lógica entre el número de artículos científicos que publica un investigador y su preferencia por un sabor de helado en particular. Como resultado, se espera que estas dos variables exhiban esta correlación.
Campo de la educación
Ejemplo: Talla de zapato de los estudiantes y sus calificaciones en matemáticas
Un estudio educativo examina si existe alguna relación entre la talla de los zapatos de los estudiantes y sus calificaciones en matemáticas.
La talla de zapato es una característica física que no tiene relación con el rendimiento académico de un estudiante en matemáticas. Por lo tanto, es probable que la correlación entre la talla de zapato y las calificaciones en matemáticas sea cero.
Campo de la Salud
Ejemplo: Tipo de sangre e incidencia del resfriado común
Un estudio de salud analiza si existe una relación entre el tipo de sangre de una persona y el número de veces que se resfría en un año.
El tipo de sangre no está asociado con la frecuencia de contraer el resfriado común, que está influenciado por varios otros factores, como la exposición a virus y la fortaleza del sistema inmunológico. Por lo tanto, se espera que la correlación entre el tipo de sangre y la incidencia del resfriado común sea cero.
¿Cómo identificar la correlación nula o cero?
Aquí, exploraremos cómo identificar esta correlación a través de la inspección visual, el cálculo estadístico, la prueba de hipótesis y el análisis contextual.
1. Inspección visual usando diagramas de dispersión
Los diagramas de dispersión son una herramienta efectiva para evaluar visualmente la relación entre dos variables.
Crear un diagrama de dispersión:
- Coloca una variable en el eje x y la otra en el eje y.
- Busca alguna tendencia o patrón discernible en los puntos de datos.
Identificación de la correlación:
- Si los puntos están dispersos al azar sin una tendencia clara (ni ascendente ni descendente), sugiere una correlación cero.
- Una dispersión aleatoria implica que ninguna línea (ya sea recta o curva) puede ajustar bien los puntos de datos.
Ejemplo:
- Tallas de zapatos de los estudiantes vs. calificaciones en matemáticas: Si trazas las tallas de zapatos contra las calificaciones en matemáticas y ves una dispersión aleatoria de puntos sin tendencia, esto indica una correlación cero.
2. Calcular el coeficiente de correlación
El coeficiente de correlación de Pearson (r) es la medida más común de la correlación lineal.
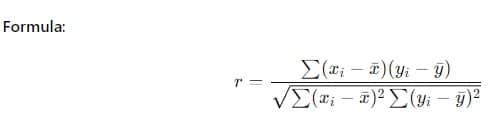
Pasos:
- Reúne puntos de datos emparejados para las dos variables.
- Encuentra la media (promedio) de cada variable.
- Calcula qué tan lejos está cada punto de datos de la media.
- Multiplica las desviaciones para cada par y suma los productos.
- Usa la fórmula para encontrar el coeficiente de correlación.
Interpretación de la correlación:
- Valor cercano a 0: Si r es cercano a 0, indica poca o ninguna relación lineal entre las variables.
Ejemplo:
- Tallas de zapatos y calificaciones en matemáticas: Si el r calculado es aproximadamente 0, confirma la correlación cero.
3. Prueba de hipótesis
La prueba de hipótesis estadística puede determinar si un coeficiente de correlación observado es significativamente diferente de cero.
Pasos:
- Hipótesis nula: Asume que el coeficiente de correlación es cero.
- Hipótesis alternativa: Asume que el coeficiente de correlación no es cero.
- Calcular el estadístico de prueba: Usa una prueba t para el coeficiente de correlación.
- Determinar el valor p: Compara el valor p con un nivel de significancia (por ejemplo, 0.05).
Correlación cero:
- Si el valor p es mayor que el nivel de significancia, no rechaces la hipótesis nula, sugiriendo que la correlación no es significativamente diferente de cero.
Ejemplo:
- Tipo de sangre e incidencia del resfriado común: Al probar la correlación entre el tipo de sangre y la incidencia del resfriado común, si el valor p es alto, indica que cualquier correlación observada no es estadísticamente significativa, apoyando la correlación cero.
4. Análisis contextual
Comprender el contexto y el trasfondo teórico de las variables es esencial para interpretar los resultados de la correlación.
Pasos:
- Examinar variables: Considera la naturaleza y las relaciones esperadas entre las variables.
- Aplicar conocimiento del campo: Usa el conocimiento del campo para hipotetizar si se espera una relación.
Correlación cero:
- Si la teoría y la investigación previa sugieren que no hay una relación lógica, esto apoya el hallazgo de esta correlación.
Ejemplo:
- Tipo de sangre e incidencia del resfriado común: Saber que el tipo de sangre no afecta la susceptibilidad al resfriado común apoya la interpretación de una correlación cero si se encuentra.
Correlación negativa vs positiva vs cero
La correlación es una medida estadística que describe la fuerza y la dirección de la relación entre dos variables. Aquí hay una explicación detallada de la correlación negativa, positiva y nula:
Correlación positiva
- Definición: Una correlación positiva ocurre cuando dos variables se mueven en la misma dirección. A medida que una variable aumenta, la otra variable también aumenta, y a medida que una disminuye, la otra también disminuye.
- Ejemplo: La relación entre la altura y el peso. Generalmente, a medida que aumenta la altura de una persona, su peso también tiende a aumentar.
- Representación gráfica: En un diagrama de dispersión, los puntos tienden a agruparse alrededor de una línea que se inclina hacia arriba de izquierda a derecha.
Correlación negativa
- Definición: Una correlación negativa ocurre cuando dos variables se mueven en direcciones opuestas. A medida que una variable aumenta, la otra variable disminuye, y viceversa.
- Ejemplo: La relación entre el tiempo dedicado a estudiar y el número de errores cometidos en un examen. Generalmente, a medida que aumenta el tiempo dedicado a estudiar, disminuye el número de errores.
- Representación gráfica: En un diagrama de dispersión, los puntos tienden a agruparse alrededor de una línea que se inclina hacia abajo de izquierda a derecha.
Correlación cero
- Definición: Indica que no hay relación entre las dos variables. Los cambios en una variable no predicen cambios en la otra.
- Ejemplo: La relación entre la talla de zapato de una persona y su coeficiente intelectual (IQ). No hay una conexión lógica entre estas dos variables.
- Representación gráfica: En un diagrama de dispersión, los puntos se distribuyen aleatoriamente sin un patrón discernible o pendiente.
¿Cómo puede QuestionPro ayudar en el análisis de correlación?
QuestionPro, una plataforma robusta de encuestas, ofrece herramientas integrales para facilitar el análisis de correlación de manera efectiva. Aquí se explica cómo QuestionPro puede ayudarte a realizar un análisis de correlación:
Recopilación de datos sin esfuerzo
QuestionPro simplifica el proceso de recopilación de datos a través de sus herramientas de creación de encuestas fáciles de usar. Puedes diseñar y distribuir encuestas para recopilar datos cuantitativos sobre varias variables de interés. La plataforma soporta diversos tipos de preguntas, lo que te permite capturar datos detallados y relevantes de manera eficiente.
Análisis de datos automatizado
Una vez que los datos se recopilan, QuestionPro proporciona herramientas analíticas integradas para el análisis de correlación. Puedes calcular fácilmente las correlaciones, que miden la fuerza y la dirección de la relación lineal entre dos variables. El coeficiente de correlación lineal varía de -1 a 1, donde:
- 1 indica una correlación positiva perfecta.
- -1 indica una correlación negativa perfecta.
- 0 indica una correlación nula.
Representación visual
QuestionPro ofrece herramientas de visualización para ayudarte a interpretar los resultados de tu análisis de correlación. Se pueden generar diagramas de dispersión y matrices de correlación para proporcionar una representación gráfica clara de las relaciones entre las variables. Esta ayuda visual es crucial para identificar rápidamente tendencias y patrones.
Identificación de patrones y tendencias
Utilizando el análisis de correlación de QuestionPro, los investigadores pueden observar correlaciones (positivas, negativas o nulas) entre variables:
- Correlación positiva: Ambas variables se mueven en la misma dirección. Por ejemplo, un aumento en el gasto publicitario puede correlacionarse con un aumento en las ventas.
- Correlación negativa: Las variables tienden a moverse en direcciones opuestas. Por ejemplo, un aumento en el tiempo de pantalla podría correlacionarse con una disminución en el rendimiento académico.
- Correlación nula: No existe relación entre las variables. Por ejemplo, el número de años en la escuela podría no correlacionarse con el número de letras en el nombre de una persona.
Aplicaciones prácticas
El análisis de correlación en QuestionPro puede utilizarse para diversas aplicaciones prácticas, tales como:
- Investigación de mercado: Medir la efectividad de las campañas de marketing correlacionando el gasto publicitario con el desempeño de ventas.
- Salud: Evaluar la relación entre el uso de medicamentos y los resultados de los pacientes, como los niveles de presión arterial.
- Educación: Determinar el impacto de los hábitos de estudio en el rendimiento académico correlacionando las horas de estudio con las calificaciones.
Conclusión
La correlación nula o correlación cero entre dos variables significa la ausencia de una relación lineal, indicando que los cambios en una variable no corresponden con cambios en otra. Al calcular los coeficientes de correlación y visualizar los datos a través de diagramas de dispersión, los investigadores pueden determinar con precisión si las variables están correlacionadas, positiva, negativa o nula.
Usar QuestionPro para el análisis de correlación en tus encuestas proporciona una forma poderosa de descubrir relaciones significativas entre variables. Al explorar la interfaz intuitiva de QuestionPro, sus herramientas analíticas avanzadas y sus completas características de informes, puedes realizar eficazmente análisis de correlación y obtener valiosas ideas de tus datos. ¡Contacta a QuestionPro hoy para obtener más información!



