Coefficient de corrélation de Spearman : Définition
Le coefficient de corrélation de rang de Spearman ou coefficient de corrélation de Spearman est une mesure non paramétrique de la corrélation de rang (dépendance statistique du rang entre deux variables).
Nommé d’après Charles Spearman, il est souvent désigné par la lettre grecque « ρ » (rho) et est principalement utilisé pour l’analyse de données.
Il mesure la force et la direction de l’association entre deux variables classées. Mais avant de parler du coefficient de corrélation de Spearman, il est important de comprendre la corrélation de Pearson. La corrélation de Pearson est une mesure statistique de la force d’une relation linéaire entre des données appariées.
Pour le calcul et le test de signification de la variable de classement, il faut que les données suivantes soient vraies :
- Niveau d’intervalle ou de rapport
- Linéaire
- Distribué bivariant
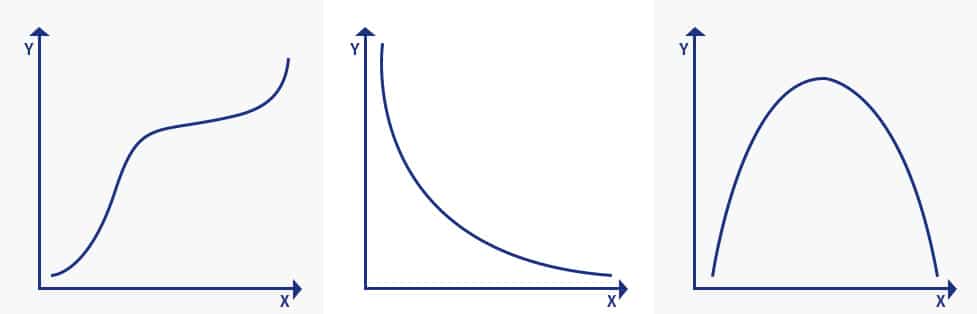
Si vos données ne répondent pas aux hypothèses ci-dessus, vous aurez besoin du coefficient de Spearman. Il est nécessaire de savoir ce qu’est une fonction monotone pour comprendre le coefficient de corrélation de Spearman. Une fonction monotone est une fonction qui soit ne diminue jamais, soit n’augmente jamais en fonction de l’augmentation de la variable indépendante. Une fonction monotone peut être expliquée à l’aide de l’image ci-dessous :
L’image explique trois concepts de la fonction monotone :
- Augmentation monotone : Lorsque la variable « x » augmente et que la variable « y » ne diminue jamais.
- Décroissance monotone : Lorsque la variable « x » augmente mais que la variable « y » n’augmente jamais.
- Non monotone : Lorsque la variable « x » augmente et que la variable « y » augmente parfois et diminue parfois.
La relation monotone est moins restrictive que la relation linéaire utilisée dans le coefficient de Pearson. Bien que la monotonicité ne soit pas l’exigence ultime du coefficient de corrélation de Spearman, il ne sera pas utile de rechercher la corrélation de Spearman sans déterminer la force et la direction d’une relation monotone si l’on sait déjà que la relation entre les variables n’est pas monotone.
En savoir plus : Analyse du gazon à l’aide d’exemples
Coefficient de corrélation de Spearman : Formule et calcul avec exemple
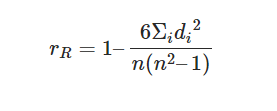
n= nombre de points de données des deux variables
di= différence de rangs du « ième » élément
Le coefficient de Spearman, ⍴, peut prendre une valeur comprise entre +1 et -1 où,
- Une valeur ⍴ de +1 signifie une association parfaite du rang
- Une valeur ⍴ de 0 signifie qu’il n’y a pas d’association entre les rangs.
- Une valeur ⍴ de -1 signifie une association négative parfaite entre les rangs.
Plus la valeur ⍴ est proche de 0, plus l’association entre les deux rangs est faible.
Nous devons être en mesure de classer les données avant de procéder au calcul du coefficient de corrélation de rang de Spearman. Il est important d’observer si, en augmentant une variable, l’autre variable suit une relation monotone.
À chaque niveau, vous devrez comparer les valeurs des deux variables. Voici comment se déroulent les calculs :
Les notes de 9 élèves en histoire et en géographie sont mentionnées dans le tableau ci-dessous.
Étape 1 – Créer un tableau des données obtenues.
Étape 2 – Commencez par classer les deux ensembles de données. Le classement des données peut être réalisé en attribuant le rang « 1 » au plus grand nombre de la colonne, « 2 » au deuxième plus grand nombre et ainsi de suite. La valeur la plus faible est généralement la moins bien classée. Cette opération doit être effectuée pour les deux séries de mesures.
Étape 3 – Ajoutez une troisième colonne d à votre ensemble de données, d représentant ici la différence entre les rangs. Par exemple, si le classement du premier étudiant en physique est de 3 et celui en mathématiques de 5, la différence de classement est de 3. Dans la quatrième colonne, élevez au carré vos valeurs d.
| L’histoire | Rang | Géographie | Rang | d | d carré |
| 35 | 3 | 30 | 5 | 2 | 4 |
| 23 | 5 | 33 | 3 | 2 | 4 |
| 47 | 1 | 45 | 2 | 1 | 1 |
| 17 | 6 | 23 | 6 | 0 | 0 |
| 10 | 7 | 8 | 8 | 1 | 1 |
| 43 | 2 | 49 | 1 | 1 | 1 |
| 9 | 8 | 12 | 7 | 1 | 1 |
| 6 | 9 | 4 | 9 | 0 | 0 |
| 28 | 4 | 31 | 4 | 0 | 0 |
| 12 |
Étape 4 – Additionnez toutes les valeurs de votre carré d, ce qui donne 12 (∑d carré).
Étape 5- Insérer ces valeurs dans la formule
=1-(6*12)/(9(81-1))
=1-72/720
=1-01
=0.9
La corrélation de rang de Spearman pour ces données est de 0,9 et, comme indiqué ci-dessus, si la valeur ⍴ est proche de +1, l’association de rang est parfaite.
En savoir plus : Analyse conjointe – Définition, types, exemple, algorithme et modèle
Comment réaliser un coefficient de corrélation avec QuestionPro
Dans cette section, vous apprendrez comment exécuter le coefficient de corrélation de rang de Spearman pour votre enquête.
Étape 1 : Allez dans Mes enquêtes →Sélectionnez Enquête→Analytique
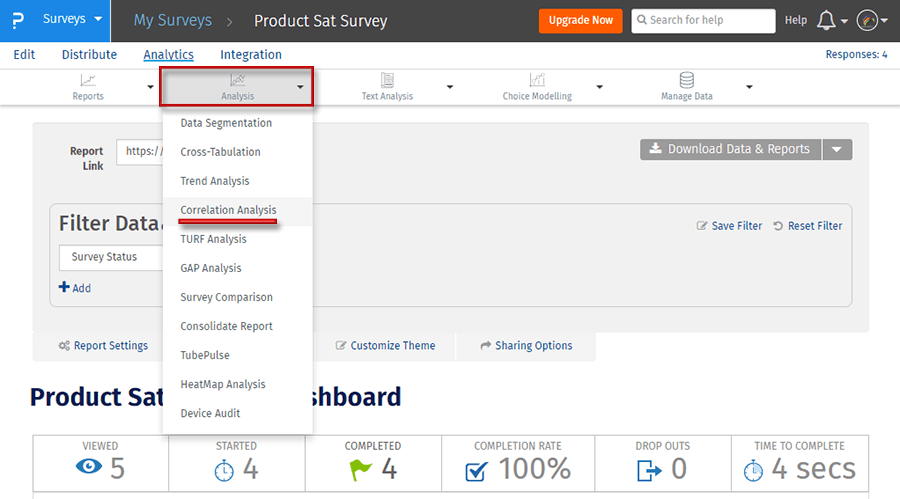
Étape 2 : Cliquez sur Analyse corrélationnelle sous Analyse
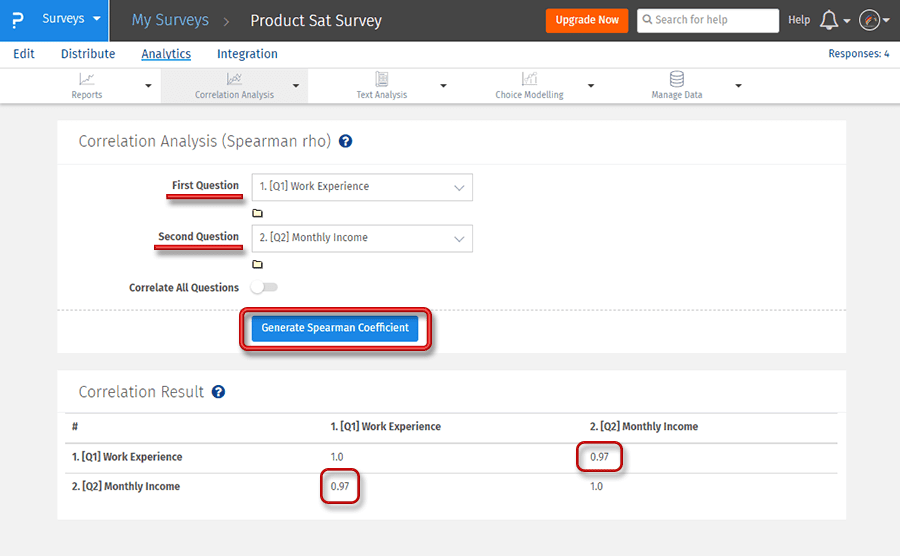
Étape 3 : Cliquez sur le bouton Générer le coefficient de Spearman pour obtenir un rapport détaillé.
Dans l’exemple ci-dessus, le coefficient de corrélation de Spearman est utilisé pour déterminer la relation entre les deux variables, l’expérience professionnelle et le revenu mensuel. D’une manière générale, le revenu mensuel devrait augmenter avec l’expérience professionnelle, ce qui signifie qu’il devrait y avoir une association positive entre les deux variables, comme le prouve la valeur rs de 0,97.
En savoir plus : Analyse des écarts – Définition, méthode et modèle avec exemple