
La corrélation est un concept fondamental des statistiques et de l’analyse des données, qui permet de comprendre la relation entre deux variables. Si les corrélations positives ou négatives fortes sont souvent mises en évidence, la corrélation nulle est tout aussi importante.
Cela signifie qu’il n’y a pas de relation linéaire entre les variables. En d’autres termes, les variations d’une variable ne permettent pas de prédire les variations de l’autre.
Dans ce blog, nous allons explorer le concept de corrélation zéro, en fournissant une définition claire, des exemples illustratifs et des méthodes pour la déterminer.
Qu’est-ce qu’une corrélation nulle ?
La corrélation zéro est un terme statistique qui décrit une situation où il n’y a pas de relation linéaire entre deux variables. Lorsque deux variables ont une corrélation nulle, les variations d’une variable ne permettent pas de prédire les variations de l’autre. Le coefficient de corrélation, qui mesure le degré et la direction de la relation entre les variables, est exactement nul dans ce cas.
La compréhension de cette corrélation est importante dans l’analyse statistique car elle permet d’identifier les variables qui n’ont pas de relation prédictive entre elles, ce qui est crucial lors de l’élaboration de modèles statistiques ou de l’interprétation de schémas de données.
Pourquoi la corrélation zéro est-elle importante ?
La corrélation zéro est un concept important dans les statistiques et l’analyse des données pour plusieurs raisons :
Il identifie l’indépendance
Elle permet d’identifier les variables qui sont linéairement indépendantes les unes des autres. Si deux variables ont une corrélation nulle, les variations d’une variable ne fournissent aucune information sur les variations de l’autre. Ceci est crucial pour comprendre la structure des données et les relations (ou l’absence de relations) entre les variables.
Elle améliore les modèles statistiques
Dans l’analyse de régression et d’autres modèles statistiques, l’inclusion de variables ayant cette corrélation avec la variable dépendante peut ajouter du bruit et réduire le pouvoir prédictif du modèle. En identifiant et en excluant ces variables, les modèles peuvent être simplifiés et rendus plus efficaces, ce qui permet d’améliorer les performances et l’interprétabilité.
Cette corrélation permet d’éviter les erreurs d’interprétation
La compréhension de cette corrélation permet d’éviter une mauvaise interprétation des données.
- Par exemple, un chercheur peut déduire à tort une relation entre deux variables sur la base d’une intuition ou d’observations initiales.
Le fait de calculer le coefficient de corrélation et de le trouver nul clarifie le fait qu’il n’existe pas de relation linéaire, ce qui permet d’éviter les fausses conclusions.
Elle met en évidence les relations non linéaires
Elle met en évidence la possibilité de relations non linéaires. Si deux variables ont une corrélation nulle, cela ne signifie pas nécessairement qu’elles ne sont pas liées ; elles peuvent avoir une relation complexe et non linéaire. La reconnaissance de cette relation peut inciter à poursuivre les recherches en utilisant d’autres méthodes, telles que la régression non linéaire ou la transformation des données.
La corrélation permet d’orienter la conception des expériences
Dans la conception d’expériences, le fait de savoir quelles variables ont une corrélation nulle peut guider la sélection des variables à inclure ou à contrôler. Cela permet de concevoir des expériences plus robustes où l’influence des variables non pertinentes est minimisée, ce qui permet d’obtenir des résultats plus clairs et plus fiables.
Il comprend les comportements variables
Elle permet de comprendre le comportement des variables d’un ensemble de données. En analyse financière, comprendre quels actifs ont une corrélation nulle entre eux peut aider à la diversification des portefeuilles, car la combinaison de ces actifs peut réduire le risque global.
Il soutient les tests d’hypothèses
Dans les tests d’hypothèses, cette corrélation est souvent une hypothèse nulle.
- Par exemple, pour vérifier si deux variables sont liées, l’hypothèse nulle peut indiquer que la corrélation entre elles est nulle.
Déterminer si cela est vrai ou faux permet de valider ou de réfuter des hypothèses.
Quels sont les exemples de corrélation nulle ?
Des exemples de cette corrélation, où les changements d’une variable ne correspondent pas aux changements d’une autre variable, peuvent être trouvés dans divers domaines tels que :
Domaine de recherche
Exemple : Nombre de publications scientifiques et parfum de glace préféré
Une étude examine la relation entre le nombre de publications scientifiques d’un chercheur et son parfum de glace préféré.
Il n’y a pas de lien logique entre le nombre d’articles scientifiques publiés par un chercheur et sa préférence pour un parfum de glace particulier. Par conséquent, on s’attend à ce que ces deux variables présentent cette corrélation.
Domaine de l’éducation
Exemple : Taille des chaussures des élèves et notes en mathématiques
Une étude pédagogique examine s’il existe un lien entre la pointure des chaussures des élèves et leurs notes en mathématiques.
La pointure est une caractéristique physique qui n’a aucune incidence sur les résultats scolaires d’un élève en mathématiques. Par conséquent, la corrélation entre la pointure et les notes en mathématiques est probablement nulle.
Domaine de la santé
Exemple : Groupe sanguin et incidence du rhume
Une étude sur les soins de santé examine s’il existe un lien entre le groupe sanguin d’une personne et le nombre de fois où elle attrape un rhume au cours d’une année.
Le groupe sanguin n’est pas associé à la fréquence du rhume, qui est influencée par divers autres facteurs tels que l’exposition aux virus et la force du système immunitaire. Par conséquent, la corrélation entre le groupe sanguin et l’incidence du rhume devrait être nulle.
Comment identifier une corrélation nulle ?
Nous verrons ici comment identifier cette corrélation par une inspection visuelle, des calculs statistiques, des tests d’hypothèses et une analyse contextuelle.
1. L’inspection visuelle à l’aide de diagrammes de dispersion
Les diagrammes de dispersion sont un outil efficace pour évaluer visuellement la relation entre deux variables.
Créez un diagramme de dispersion :
- Placez une variable sur l’axe des x et l’autre sur l’axe des y.
- Recherchez une tendance ou un modèle perceptible dans les points de données.
Identifier la corrélation :
- Si les points sont dispersés de manière aléatoire sans tendance claire (ni à la hausse ni à la baisse), cela suggère une corrélation.
- Une dispersion aléatoire implique qu’aucune ligne (qu’elle soit droite ou courbe) ne peut s’adapter correctement aux points de données.
Exemple :
- Taille des chaussures des élèves par rapport à leurs notes en mathématiques : Si vous représentez les pointures de chaussures par rapport aux notes de mathématiques et que vous observez une dispersion aléatoire de points sans tendance, cela indique une corrélation nulle.
2. Calculez le coefficient de corrélation
Le coefficient de corrélation de Pearson (r) est la mesure la plus courante de la corrélation linéaire.
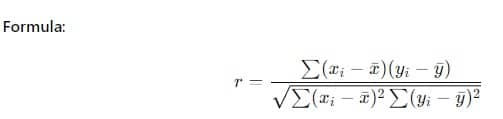
Les étapes :
- Rassemblez des points de données appariés pour les deux variables.
- Trouvez la moyenne de chaque variable.
- Calculez la distance qui sépare chaque point de données de la moyenne.
- Multipliez les écarts pour chaque paire et additionnez les produits.
- Utilisez la formule pour trouver le coefficient de corrélation.
Interprétation de la corrélation :
Valeur proche de 0 : Si 𝑟 r est proche de 0, cela indique une relation linéaire faible ou nulle entre les variables.
Exemple :
- Pointures de chaussures et notes de mathématiques : Si le 𝑟 calculé est approximativement égal à 0, cela confirme une corrélation nulle.
3. Effectuez le test d’hypothèse
Les tests d’hypothèses statistiques permettent de déterminer si un coefficient de corrélation observé est significativement différent de zéro.
Les étapes :
- Hypothèse nulle : Supposez que le coefficient de corrélation est nul.
- Hypothèse alternative : Supposez que le coefficient de corrélation n’est pas nul.
- Calcul de la statistique de test : utilisez un test t pour le coefficient de corrélation.
- Déterminez la valeur p : Comparez la valeur p à un niveau de signification (par exemple, 0,05).
Corrélation zéro :
- Si la valeur p est supérieure au seuil de signification, ne rejetez pas l’hypothèse nulle, ce qui suggère que la corrélation n’est pas significativement différente de zéro.
Exemple :
- Groupe sanguin et incidence du rhume : En testant la corrélation entre le groupe sanguin et l’incidence du rhume, si la valeur p est élevée, cela indique que toute corrélation observée n’est pas statistiquement significative, ce qui plaide en faveur d’une corrélation nulle.
4. Comprendre l’analyse contextuelle
Il est essentiel de comprendre le contexte et l’arrière-plan théorique des variables pour interpréter les résultats des corrélations.
Les étapes :
- Examinez les variables : Examinez la nature et les relations attendues entre les variables.
- Appliquer les connaissances du domaine : Utilisez les connaissances acquises dans le domaine pour émettre des hypothèses sur l’existence d’une relation.
Corrélation zéro :
- Si la théorie et les recherches antérieures ne suggèrent aucune relation logique, cela soutient la conclusion de cette corrélation.
Exemple :
- Groupe sanguin et incidence du rhume : Le fait de savoir que le groupe sanguin n’a pas d’incidence sur la sensibilité au rhume conforte l’interprétation d’une corrélation nulle, le cas échéant.
Corrélation négative ou positive ou corrélation nulle
La corrélation est une mesure statistique qui décrit la force et la direction de la relation entre deux variables. Voici une explication détaillée de la corrélation négative, positive et nulle :
Corrélation positive
- Définition : Une corrélation positive se produit lorsque deux variables évoluent dans la même direction. Lorsqu’une variable augmente, l’autre augmente également, et lorsqu’une variable diminue, l’autre diminue également.
- Exemple : La relation entre la taille et le poids. En général, plus une personne est grande, plus son poids a tendance à augmenter.
- Représentation graphique : Dans un diagramme de dispersion, les points ont tendance à se regrouper autour d’une ligne qui s’élève de gauche à droite.
Corrélation négative
- Définition : Une corrélation négative se produit lorsque deux variables évoluent dans des directions opposées. Lorsqu’une variable augmente, l’autre diminue, et vice versa.
- Exemple : La relation entre le temps passé à étudier et le nombre d’erreurs commises lors d’un test. En général, plus le temps consacré à l’étude augmente, plus le nombre d’erreurs diminue.
- Représentation graphique : Dans un diagramme de dispersion, les points ont tendance à se regrouper autour d’une ligne qui descend de gauche à droite.
Corrélation nulle
- Définition : Elle indique qu’il n’y a pas de relation entre les deux variables. Les variations d’une variable ne permettent pas de prédire les variations de l’autre variable.
- Exemple : La relation entre la pointure d’une personne et son quotient intellectuel (QI). Il n’y a pas de lien logique entre ces deux variables.
- Représentation graphique : Dans un diagramme de dispersion, les points sont distribués de manière aléatoire, sans tendance ou pente perceptible.
Comment QuestionPro peut aider à l’analyse de corrélation ?
QuestionPro, une plateforme d’enquête robuste, offre des outils complets pour faciliter l’analyse de corrélation de manière efficace. Voici comment QuestionPro peut vous aider à réaliser une analyse de corrélation :
Collecte de données sans effort
QuestionPro simplifie le processus de collecte de données grâce à ses outils conviviaux de création d’enquêtes. Vous pouvez concevoir et distribuer des enquêtes pour recueillir des données quantitatives sur diverses variables d’intérêt. La plateforme prend en charge différents types de questions, ce qui vous permet de recueillir efficacement des données détaillées et pertinentes.
Analyse automatisée des données
Une fois les données collectées, QuestionPro fournit des outils analytiques intégrés pour l’analyse des corrélations. Vous pouvez facilement calculer les corrélations, qui mesurent la force et la direction de la relation linéaire entre deux variables. Le coefficient de corrélation linéaire est compris entre -1 et 1, où :
- 1 indique une corrélation positive parfaite.
- -1 indique une corrélation négative parfaite.
- 0 indique qu’il n’y a pas de corrélation.
Représentation visuelle
QuestionPro propose des outils de visualisation pour vous aider à interpréter les résultats de votre analyse de corrélation. Des diagrammes de dispersion et des matrices de corrélation peuvent être générés pour fournir une représentation graphique claire des relations entre les variables. Cette aide visuelle est cruciale pour identifier rapidement les tendances et les modèles.
Identifier les modèles et les tendances
En utilisant l’analyse de corrélation de QuestionPro, les chercheurs ont observé la corrélation (positive, négative ou nulle) entre les variables :
- Corrélation positive : Les deux variables évoluent dans le même sens. Par exemple, l’augmentation des dépenses publicitaires peut être corrélée à l’augmentation des ventes.
- Corrélation négative : Les variables ont tendance à évoluer dans des directions opposées. Par exemple, l’augmentation du temps passé devant un écran peut être corrélée à une baisse des résultats scolaires.
- Corrélation nulle : Il n’existe aucune relation entre les variables. Par exemple, il n’y a pas de corrélation entre le nombre d’années d’études et le nombre de lettres du nom d’une personne.
Applications pratiques
L’analyse de corrélation dans QuestionPro peut être utilisée pour diverses applications pratiques, telles que
- Études de marché : Mesurez l’efficacité des campagnes de marketing en établissant une corrélation entre les dépenses publicitaires et les résultats des ventes.
- Soins de santé : Évaluez la relation entre l’utilisation des médicaments et les résultats pour les patients, tels que les niveaux de tension artérielle.
- Éducation : Déterminez l’impact des habitudes d’étude sur les résultats scolaires en établissant une corrélation entre les heures étudiées et les notes.
Conclusion
Une corrélation nulle entre deux variables signifie l’absence de relation linéaire, indiquant que les changements d’une variable ne correspondent pas aux changements d’une autre. En calculant les coefficients de corrélation et en visualisant les données à l’aide de diagrammes de dispersion, les chercheurs peuvent déterminer avec précision si les variables sont corrélées, positivement corrélées, négativement corrélées ou si elles présentent cette corrélation.
L’utilisation de QuestionPro pour l’analyse des corrélations dans vos enquêtes constitue un moyen puissant de découvrir des relations significatives entre les variables. En explorant l’interface intuitive de QuestionPro, ses outils analytiques avancés et ses fonctions de rapport complètes, vous pouvez mener efficacement des analyses de corrélation et tirer de précieuses informations de vos données. Contactez QuestionPro dès aujourd’hui pour plus d’informations !







