Marktforschung
Gaußsche Glocke: Was sie ist und Merkmale
sdcsdcsdcsdvsdv
KOSTENEFFIZIENT
ONLINE & OFFLINE
SCHNELLER ROLL-OUT
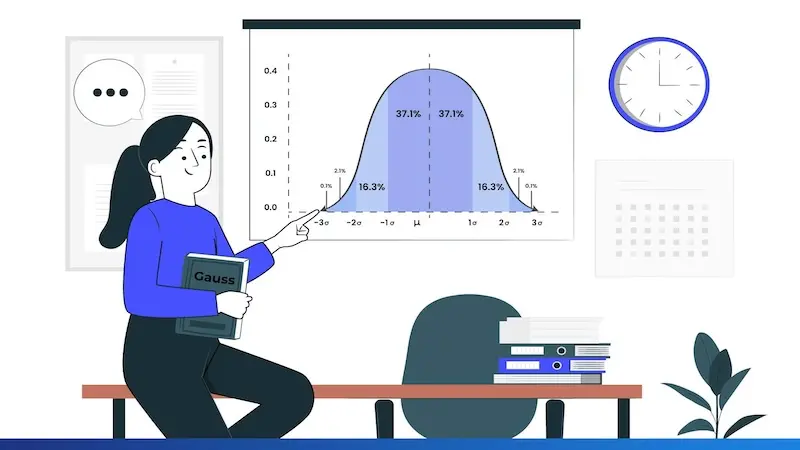
Die Gaußsche Glocke, auch bekannt als Normalverteilung, ist nach dem deutschen Mathematiker Carl Friedrich Gauß benannt und hat sich zu einer wesentlichen Säule der statistischen Analyse entwickelt, die in einer Vielzahl von Disziplinen verwendet wird.
In diesem Artikel wird die Gaußsche Glocke von ihrer Definition bis hin zu ihren praktischen Anwendungen untersucht, wobei ihre Vorteile und besonderen Merkmale hervorgehoben werden.
Was ist eine Gaußsche Glocke?
Die Gaußsche Glocke oder Normalverteilung ist eine mathematische Funktion, die die Verteilung von Daten in einer Menge beschreibt. Sie zeichnet sich durch ihre symmetrische Form und das berühmte glockenförmige Aussehen aus, wobei die meisten Daten um den Mittelwert konzentriert sind und sich gleichmäßig zu beiden Seiten verteilen. Die Funktion wird durch zwei Hauptparameter definiert: den Mittelwert, der das Zentrum der Verteilung darstellt, und die Standardabweichung, die die Streuung der Daten misst.
Ihre symmetrische Form bedeutet, dass die Hälfte der Daten links vom Mittelwert und die Hälfte rechts davon liegt. Außerdem liegen etwa 68 % der Daten innerhalb einer Standardabweichung vom Mittelwert, während 95 % innerhalb von zwei Standardabweichungen liegen.
Ein weiteres interessantes Merkmal ist, dass die Verteilung unabhängig von der Form der ursprünglichen Verteilung dazu neigt, einer Gauß’schen Glockenform zu folgen, wenn genügend Daten akkumuliert werden. Dieses Phänomen ist als zentraler Grenzwertsatz bekannt, der die weite Verbreitung dieser Verteilung in der statistischen Analyse unterstreicht.
Vorteile der Gaußschen Glocke: Warum ist sie so leistungsfähig?
Die Popularität der Gaußschen Glocke beruht auf mehreren entscheidenden Vorteilen. Erstens ist sie äußerst intuitiv und leicht verständlich, so dass sie auch für Personen ohne umfassende mathematische Vorkenntnisse ein zugängliches Werkzeug ist. Darüber hinaus kann sie aufgrund ihrer breiten Anwendbarkeit ein breites Spektrum an realen Situationen genau modellieren.
Ein weiterer entscheidender Vorteil ist seine Fähigkeit, Informationen in zwei Parametern zusammenzufassen: dem Mittelwert und der Standardabweichung. Dies vereinfacht die Datenanalyse und -interpretation erheblich und ermöglicht es Forschern und Analysten, wertvolle Informationen effizient zu erhalten.
Der zentrale Grenzwertsatz besagt, dass sich die Verteilung der Stichprobenmittelwerte bei einem ausreichend großen Stichprobenumfang einer Normalverteilung annähert, unabhängig von der Form der ursprünglichen Verteilung. Dies macht die Gaußsche Glocke zu einem leistungsfähigen Instrument für die Analyse großer Datensätze.
Die Gaußsche Glocke ist von zentraler Bedeutung für viele statistische Tests, wie z. B. den t-Test und den Chi-Quadrat-Test. Diese Tests beruhen auf der Annahme der Normalität, um Rückschlüsse auf Populationen zu ziehen.
Anwendungen der Gaußschen Glocke
Die Gaußsche Glocke wird in einer Vielzahl von Bereichen eingesetzt, von der Physik und Biologie bis hin zu Wirtschaft und Psychologie. In der Statistik wird sie häufig zur Modellierung natürlicher Phänomene verwendet, z. B. der Größe einer Bevölkerung oder von Testergebnissen. Darüber hinaus wird diese Verteilung als Grundlage für andere statistische Instrumente und komplexere Modelle verwendet.
Die Gaußsche Glocken- oder Normalverteilung wird aufgrund ihrer Vielseitigkeit und ihrer Fähigkeit, zahlreiche Phänomene zu modellieren, in einer Vielzahl von Bereichen eingesetzt. Einige der häufigsten Anwendungen sind:
Deskriptive Statistik:
Die Gaußsche Glocke ist grundlegend für die Beschreibung der Verteilung von Daten in einer Population. Sie wird verwendet, um die zentrale Tendenz und Streuung eines Datensatzes zusammenzufassen und zu verstehen.
Statistische Schlussfolgerungen:
Bei statistischen Schlussfolgerungen ist die Gaußsche Glocke entscheidend für Vorhersagen und Schätzungen. Sie ermöglicht die Berechnung von Konfidenzintervallen und die Durchführung von Hypothesen-Tests und bietet damit grundlegende Werkzeuge für die datengestützte Entscheidungsfindung.
Psychologische Forschung:
In der Psychologie wird die Gaußsche Glocke verwendet, um verschiedene Phänomene zu modellieren, z. B. die Verteilung von Intelligenzquotienten (IQ) in einer Population. Sie wird auch in Verhaltensstudien und bei der Analyse von psychometrischen Testergebnissen verwendet.
Wirtschaft und Finanzen:
In den Wirtschafts- und Finanzwissenschaften wird die Gaußsche Glocke verwendet, um die Variabilität der Renditen von Finanzanlagen zu modellieren. Das Modell der logarithmischen Rendite folgt in vielen Fällen einer Normalverteilung, was die Risikobewertung und Investitionsentscheidungen erleichtert.
Biologie und Medizin:
In der Biologie findet man die Normalverteilung bei Phänomenen wie der Körpergröße einer Population oder der Gewichtsverteilung innerhalb einer Art. In der Medizin wird sie u. a. zur Analyse biometrischer Daten und zur Bewertung der Wirksamkeit von Behandlungen verwendet.
Qualitätskontrolle:
Die Gaußsche Glocke wird in der Qualitätskontrolle verwendet, um die Konsistenz und Variabilität bei der Produktion von Waren und Dienstleistungen zu bewerten. Sie ermöglicht es, Toleranzgrenzen festzulegen und mögliche Abweichungen in Fertigungsprozessen zu erkennen.
Modellierung von Naturphänomenen:
In verschiedenen wissenschaftlichen Disziplinen wie Physik, Meteorologie und Geologie wird die Gaußsche Glocke zur Modellierung der Verteilung von Variablen wie Windgeschwindigkeit, Temperatur oder der Konzentration von Chemikalien in einem bestimmten Gebiet verwendet.
Maschinelles Lernen und Datenwissenschaft:
Im Bereich des maschinellen Lernens wird die Gaußsche Glocke als Ausgangsannahme in vielen Algorithmen und Modellen verwendet. Außerdem wird üblicherweise angenommen, dass Vorhersagefehler einer Normalverteilung folgen, was die Entwicklung und Interpretation von Modellen erleichtert.
Beispiel einer Gaußschen Glocke: Bewertung der schulischen Leistungen
Stellen wir uns vor, wir analysieren die schulischen Leistungen der Schüler einer Sekundarschule. Wir wollen verstehen, wie die Noten in einer Mathematikprüfung verteilt sind, und verwenden die Gaußsche Glocke, um wertvolle Informationen über die Gesamtleistung der Klasse zu erhalten.
Schritt 1: Datenerhebung
Wir erheben die Noten aller Schüler im Mathematiktest. Angenommen, wir haben die folgenden Noten auf einer Skala von 0 bis 100 gesammelt:
78, 82, 85, 88, 90, 92, 94, 96, 98, 100
Schritt 2: Berechnung von Mittelwert und Standardabweichung
Wir berechnen den Mittelwert und die Standardabweichung dieser Bewertungen. Nehmen wir an, der Mittelwert ist 90 und die Standardabweichung beträgt 6. Diese Werte dienen lediglich zur Veranschaulichung des Beispiels; in einem realen Szenario würden sie anhand der tatsächlichen Daten berechnet werden.
Schritt 3: Erstellen der Gaußschen Glocke
Mit dem Mittelwert und der Standardabweichung können wir die Gauß’sche Glocke erstellen, die die Verteilung der Noten beschreibt. Die meisten Schüler konzentrieren sich um den Mittelwert herum, und die Glockenform spiegelt die Wahrscheinlichkeit wider, unterschiedliche Noten zu erhalten.
Schritt 4: Interpretation der Gaußschen Glocke
68% der Schüler: Etwa 68 % der Schüler werden innerhalb einer Standardabweichung vom Mittelwert liegen, d. h. zwischen 84 und 96 Punkten.
95% der Schüler: Etwa 95% der Schüler werden Noten innerhalb von zwei Standardabweichungen des Mittelwerts haben, d.h. im Bereich von 78 bis 102.
99,7 % der Schüler: Fast alle Schülerinnen und Schüler (99,7 %) erreichen Noten innerhalb von drei Standardabweichungen des Mittelwerts, also zwischen 72 und 108.
Schritt 5: Entscheidungsfindung und Leistungsbewertung
Anhand dieser Verteilung können Pädagogen fundierte Entscheidungen über die Wirksamkeit von Tests und Unterricht treffen. Wenn zum Beispiel eine große Anzahl von Schülern unter dem Mittelwert liegt, könnte dies auf Bereiche hinweisen, in denen der Unterricht verbessert werden muss. Darüber hinaus liefert die Gaußsche Glocke ein klares Bild von der Verteilung der Noten, was bei der Festlegung von Leistungsstandards und Bildungsrichtlinien hilfreich sein kann.
In diesem Anwendungsfall liefert die Gaußsche Glocke nicht nur eine visuelle Zusammenfassung der Notenverteilung, sondern bietet auch wertvolle Werkzeuge für Bildungsentscheidungen auf der Grundlage statistischer Daten. Dieses Beispiel veranschaulicht, wie die Normalverteilung ein leistungsfähiges Instrument für die Bewertung und kontinuierliche Verbesserung der schulischen Leistungen sein kann.
Fazit
Zusammenfassend lässt sich sagen, dass die Gaußsche Glocke mehr als nur eine mathematische Kurve ist; sie ist ein wichtiges Werkzeug, das sich in einer Vielzahl von Disziplinen als nützlich erwiesen hat. Ihre Einfachheit, Vielseitigkeit und Fähigkeit, komplexe Daten zu Schlüsselparametern zusammenzufassen, machen sie zu einem grundlegenden Bestandteil der statistischen Analyse. Während wir die Welt um uns herum weiter erforschen und verstehen, wird die Gaußsche Glocke auch weiterhin eine entscheidende Rolle für unsere Fähigkeit spielen, Phänomene mit Präzision und Klarheit zu modellieren und zu verstehen.
Wenn Sie auf der Suche nach Tools sind, mit denen Sie hochwertige Daten für Ihre nächsten Projekte sammeln können, können Sie sich an QuestionPro wenden. Beginnen Sie mit der Erstellung eines kostenlosen Kontos für unsere Umfrage-Software und entdecken Sie ihr volles Potenzial.
1:1 Live Online-Präsentation:
QUESTIONPRO MARKTFORSCHUNGS-SOFTWARE
Vereinbaren Sie einen individuellen Termin und entdecken Sie unsere Marktforschungs-Software.
[av_codeblock wrapper_element=“ wrapper_element_attributes=“ codeblock_type=“ alb_description=“ id=“ custom_class=“ av_uid=’av-lqdk2j48′]
[hubspot type=“form“ portal=“354042″ id=“3fc88fee-0142-4353-abec-d6718f1ba782″]
[/av_codeblock]
Software für Marktforschung und Experience Management jetzt 10 Tage kostenlos testen!
Sie haben Fragen zum Inhalt dieses Blogs? Kontaktieren Sie uns ganz einfach über das Kontaktformular. Wir freuen uns auf den Dialog mit Ihnen! Testen Sie zudem QuestionPro 10 Tage kostenlos und ohne Risiko in aller Ruhe und Tiefe!
Testen Sie jetzt 10 Tage kostenfrei die agile Marktforschungs- und Experience Management Plattform für qualitative und quantitative Datenerhebung und Datenanalyse von QuestionPro
WEITERFÜHRENDE STICHWORTE
DIESEN ARTIKEL TEILEN
STICHWÖRTER DIESES BLOG-BEITRAGS
Gaußsche Glocke | Marktforschung | Statistik
- Quantitative und qualitative Marktforschung durchführen mit QuestionPro (Qual & Quant)
- Marktforschung: Beispiele, Tipps, Datenerhebung, Datenanalyse, Software zur Durchführung und Darstellung der Ergebnisse
- Der große QuestionPro-Guide zum Thema Kundenbefragung: Definition, Entwicklung, Methoden, Beispiele, Auswertung, Vorlage für den Import.
- Customer Experience Management: Tipps, Tools, Best Practices
- Reputationsmanagement: Tipps, Software, App
- Sentiment Analysen und semantische Textanalyse auf Basis künstlicher Intelligenz
- Alle Infos zur Experience Management Plattform QuestionPro
- Mitarbeiterbefragungen durchführen: Ein Fachartikel von QuestionPro
