ניתוח רגרסיה הוא אולי אחת השיטות הסטטיסטיות הנפוצות ביותר לחקירה או הערכה של הקשר בין קבוצה של משתנים בלתי תלויים ותלויים. בניתוח סטטיסטי, הבחנה בין נתונים קטגוריאליים לנתונים מספריים היא חיונית, שכן נתונים קטגוריים כוללים קטגוריות או תוויות נפרדות, בעוד שנתונים מספריים מורכבים מכמויות מדידות.
הוא משמש גם כמונח כולל לטכניקות ניתוח נתונים שונות המשמשות בשיטת מחקר איכותנית למידול וניתוח משתנים רבים. בשיטת הרגרסיה, המשתנה התלוי הוא מנבא או אלמנט מסביר, והמשתנה התלוי הוא התוצאה או התגובה לשאילתה מסוימת.
למד על: שיטות ניתוח סטטיסטיות
הגדרת ניתוח רגרסיה
ניתוח רגרסיה משמש לעתים קרובות כדי למדל או לנתח נתונים. רוב מנתחי הסקר משתמשים בו כדי להבין את הקשר בין המשתנים, אשר ניתן להשתמש בו עוד יותר כדי לחזות את התוצאה המדויקת.
לדוגמה – נניח שחברת משקאות קלים רוצה להרחיב את יחידת הייצור שלה למיקום חדש יותר. לפני שנתקדם, החברה רוצה לנתח את מודל ייצור ההכנסות שלה ואת הגורמים השונים שעשויים להשפיע עליו. לפיכך, החברה עורכת סקר מקוון עם שאלון ספציפי.
לאחר שימוש בניתוח רגרסיה, קל יותר לחברה לנתח את תוצאות הסקר ולהבין את הקשר בין משתנים שונים כמו חשמל והכנסות – כאן, ההכנסות הן המשתנה התלוי.
למד על: רמת ניתוח
בנוסף, הבנת הקשר בין משתנים בלתי תלויים שונים כמו תמחור, מספר עובדים ולוגיסטיקה לבין ההכנסות מסייעת לחברה להעריך את ההשפעה של גורמים מגוונים על המכירות והרווחים.
חוקרי סקרים משתמשים לעתים קרובות בטכניקה זו כדי לבחון ולמצוא מתאם בין משתנים שונים של עניין. הוא מספק הזדמנות לאמוד את ההשפעה של משתנים בלתי תלויים שונים על משתנה תלוי.
בסך הכל, ניתוח רגרסיה חוסך את המאמצים הנוספים של חוקרי הסקר בארגון מספר משתנים בלתי תלויים בטבלאות ובבדיקה או חישוב השפעתם על משתנה תלוי. סוגים שונים של שיטות מחקר אנליטיות נמצאים בשימוש נרחב כדי להעריך רעיונות עסקיים חדשים ולקבל החלטות מושכלות.
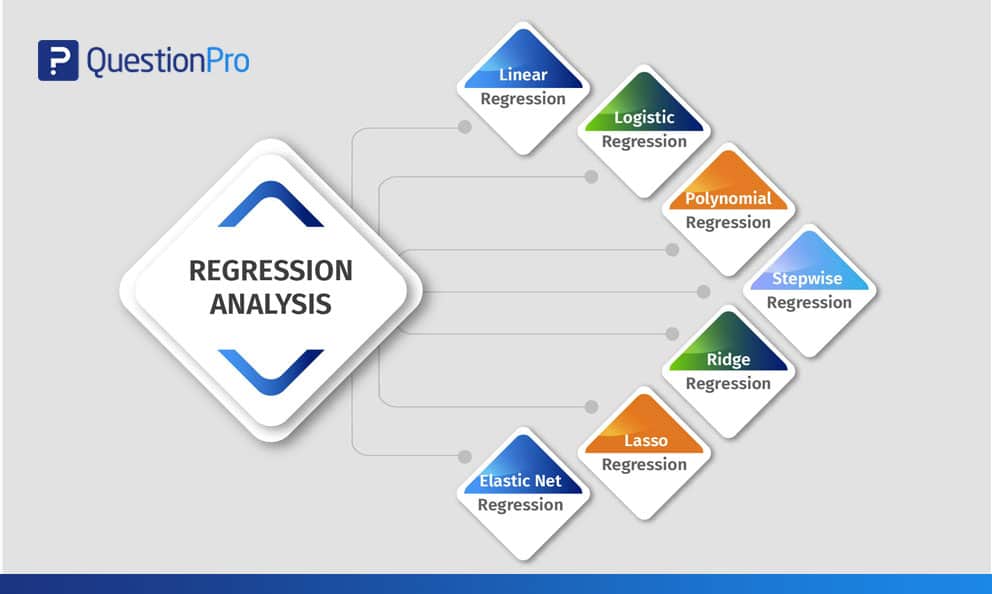
סוגי ניתוח רגרסיה
חוקרים בדרך כלל מתחילים ללמוד תחילה רגרסיה ליניארית ולוגיסטית. בשל הידע הנרחב של שתי שיטות אלה וקלות היישום, אנליסטים רבים חושבים שיש רק שני סוגים של מודלים. לכל דגם יש מומחיות משלו ויכולת לבצע אם מתקיימים תנאים ספציפיים.
בלוג זה מסביר את שבעת הסוגים הנפוצים של שיטות ניתוח רגרסיה מרובות שניתן להשתמש בהן כדי לפרש את הנתונים המנויים בפורמטים שונים.
01. ניתוח רגרסיה ליניארית
זוהי אחת מטכניקות המידול הידועות ביותר, שכן היא בין שיטות ניתוח הרגרסיה האליטה הראשונות שנאספו על ידי אנשים בזמן לימוד מודלים מנבאים. כאן, המשתנה התלוי הוא רציף, והמשתנה הבלתי תלוי הוא לעתים קרובות יותר רציף או דיסקרטי עם קו רגרסיה ליניארי.
שים לב כי לרגרסיה ליניארית מרובה יש יותר ממשתנה בלתי תלוי אחד מאשר לרגרסיה ליניארית פשוטה. לכן, רגרסיה ליניארית היא הטובה ביותר לשמש רק כאשר יש קשר ליניארי בין משתנה עצמאי תלוי.
דוגמה
עסק יכול להשתמש ברגרסיה ליניארית כדי למדוד את האפקטיביות של מסעות שיווק, תמחור ומבצעים על מכירות של מוצר. נניח שחברה שמוכרת ציוד ספורט רוצה להבין אם הכספים שהם השקיעו בשיווק ובמיתוג של המוצרים שלהם נתנו להם תשואות משמעותיות או לא.
רגרסיה ליניארית היא השיטה הסטטיסטית הטובה ביותר לפרש את התוצאות. הדבר הטוב ביותר ברגרסיה ליניארית הוא שהיא מסייעת גם בניתוח ההשפעה המעורפלת של כל פעילות שיווק ומיתוג, אך עם זאת שולטת בפוטנציאל של המרכיב לווסת את המכירות.
אם החברה מפעילה שני מסעות פרסום או יותר בו זמנית, אחד בטלוויזיה ושניים ברדיו, אז רגרסיה ליניארית יכולה בקלות לנתח את ההשפעה העצמאית והמשולבת של הפעלת פרסומות אלה יחד.
למד על: פרויקטים של ניתוח נתונים
02. ניתוח רגרסיה לוגיסטית
רגרסיה לוגיסטית משמשת בדרך כלל כדי לקבוע את ההסתברות להצלחת האירוע וכישלון האירוע. רגרסיה לוגיסטית משמשת בכל פעם שהמשתנה התלוי הוא בינארי, כגון 0/1, True/False או Yes/No. לפיכך, ניתן לומר כי רגרסיה לוגיסטית משמשת לניתוח השאלות הקרובות בסקר או השאלות הדורשות תשובות מספריות בסקר.
שימו לב שרגרסיה לוגיסטית אינה זקוקה לקשר ליניארי בין משתנה תלוי למשתנה בלתי תלוי, בדיוק כמו רגרסיה ליניארית. רגרסיה לוגיסטית מחילה טרנספורמציית יומן לא ליניארית לחיזוי יחס הסיכויים; לכן, הוא מטפל בקלות בסוגים שונים של יחסים בין משתנה תלוי ובלתי תלוי.
דוגמה
רגרסיה לוגיסטית נמצאת בשימוש נרחב לניתוח נתונים קטגוריים, במיוחד עבור נתוני תגובה בינארית במידול נתונים עסקיים. לעתים קרובות יותר, רגרסיה לוגיסטית משמשת כאשר המשתנה התלוי הוא קטגורי, כמו לחזות אם הטענה הבריאותית של אדם היא אמיתית(1) או הונאה, כדי להבין אם הגידול הוא ממאיר(1) או לא.
עסקים משתמשים ברגרסיה לוגיסטית כדי לחזות אם הצרכנים בדמוגרפיה מסוימת ירכשו את המוצר שלהם או יקנו מהמתחרים על בסיס גיל, הכנסה, מין, גזע, מדינת מגורים, רכישה קודמת וכו '.
03. ניתוח רגרסיה פולינומית
רגרסיה פולינומית משמשת בדרך כלל לניתוח נתונים עקומים כאשר כוחו של משתנה בלתי תלוי הוא יותר מ-1. בשיטת ניתוח רגרסיה זו, הקו המתאים ביותר לעולם אינו "קו ישר" אלא תמיד "קו עקומה" המתאים לנקודות הנתונים.
שים לב כי רגרסיה פולינומית עדיף להשתמש כאשר שני משתנים או יותר יש מעריכים וכמה לא.
בנוסף, הוא יכול למדל נתונים שאינם ניתנים להפרדה ליניארית ומציע את החופש לבחור את המעריך המדויק עבור כל משתנה, וגם זאת עם שליטה מלאה על תכונות המידול הזמינות.
דוגמה
בשילוב עם ניתוח משטח תגובה, רגרסיה פולינומית נחשבת לאחת השיטות הסטטיסטיות המתוחכמות הנפוצות במחקר משוב מרובה מקורות. רגרסיה פולינומית משמשת בעיקר בתעשיות פיננסיות וביטוחיות שבהן הקשר בין משתנים תלויים ובלתי תלויים הוא עקלקל.
נניח שאדם רוצה לתקצב תכנון הוצאות על ידי קביעת כמה זמן ייקח להרוויח סכום סופי. רגרסיה פולינומית, על ידי התחשבות בהכנסותיו וחיזוי הוצאות, יכולה לקבוע בקלות את הזמן המדויק שהוא / היא צריכים לעבוד כדי להרוויח את הסכום הספציפי הזה.
04. ניתוח רגרסיה מדורגת
זהו תהליך חצי אוטומטי שבו מודל סטטיסטי נבנה על ידי הוספה או הסרה של המשתנה התלוי על t-סטטיסטיקה של המקדמים המשוערים שלהם.
אם נעשה שימוש נכון, הרגרסיה המדורגת תספק לך נתונים חזקים יותר בקצות אצבעותיך מכל שיטה. זה עובד טוב כאשר אתה עובד עם מספר רב של משתנים בלתי תלויים. זה פשוט מכוונן את יחידת מודל הניתוח על ידי חיטוט משתנים באופן אקראי.
ניתוח רגרסיה מדורגת מומלץ להשתמש כאשר ישנם משתנים בלתי תלויים מרובים, שבו הבחירה של משתנים בלתי תלויים נעשה באופן אוטומטי ללא התערבות אנושית.
שים לב, במידול רגרסיה הדרגתית, המשתנה מתווסף או מופחת מקבוצת המשתנים המסבירים . קבוצת המשתנים שנוספו או הוסרו נבחרת בהתאם לסטטיסטיקת הבדיקה של המקדם המשוער.
דוגמה
נניח שיש לך קבוצה של משתנים בלתי תלויים כמו גיל, משקל, שטח פני הגוף, משך יתר לחץ דם, דופק בסיסי, ומדד מתח שעל בסיסו אתה רוצה לנתח את השפעתו על לחץ הדם.
ברגרסיה מדורגת, תת-הקבוצה הטובה ביותר של המשתנה הבלתי תלוי נבחרת באופן אוטומטי; הוא מתחיל בבחירת אף משתנה כדי להמשיך הלאה (מכיוון שהוא מוסיף משתנה אחד בכל פעם) או מתחיל עם כל המשתנים במודל וממשיך אחורה (מסיר משתנה אחד בכל פעם).
לכן, באמצעות ניתוח רגרסיה, אתה יכול לחשב את ההשפעה של כל או קבוצה של משתנים על לחץ הדם.
05. ניתוח רגרסיה רכס
רגרסיה של רכס מבוססת על שיטה רגילה הכי פחות ריבועית המשמשת לניתוח נתוני מולטיקולינאריות (נתונים שבהם משתנים בלתי תלויים מתואמים מאוד). קולינאריות יכולה להיות מוסברת כקשר כמעט ליניארי בין משתנים.
בכל פעם שיש מולטיקולינאריות, האומדנים של הריבועים הפחותים יהיו בלתי מוטים, אבל אם ההבדל ביניהם גדול יותר, אז זה עשוי להיות רחוק מהערך האמיתי. עם זאת, רגרסיה רכס מבטלת את שגיאות התקן על ידי הוספת מידה מסוימת של הטיה לאומדני הרגרסיה עם מניע לספק הערכות אמינות יותר.
אם תרצה, תוכל גם ללמוד על הטיית הבחירה דרך הבלוג שלנו.
שימו לב, הנחות הנגזרות מרגרסיה של הרכס דומות לרגרסיה הכי פחות בריבוע, ההבדל היחיד הוא הנורמליות. למרות שערך המקדם מוגבל ברגרסיה של הרכס, הוא לעולם אינו מגיע לאפס דבר המצביע על חוסר היכולת לבחור משתנים.
דוגמה
נניח שאתה משוגע על שני גיטריסטים שמופיעים בהופעה חיה באירוע קרוב אליך, ואתה הולך לצפות בהופעה שלהם עם מניע כדי לגלות מי גיטריסט טוב יותר. אבל כשההופעה מתחילה, אתה שם לב ששניהם מנגנים תווים בשחור-כחול בו זמנית.
האם ניתן למצוא את הגיטריסט הטוב ביותר שיש לו את ההשפעה הגדולה ביותר על הצליל ביניהם כאשר שניהם מנגנים חזק ומהיר? מכיוון ששניהם מנגנים תווים שונים, קשה מאוד להבדיל ביניהם, מה שהופך אותו למקרה הטוב ביותר של multicollinearity, אשר נוטה להגדיל את שגיאות התקן של המקדמים.
רגרסיה רגרסיונית מתייחסת לרב-קולינאריות במקרים כאלה וכוללת הטיה או הערכת כיווץ כדי לגזור תוצאות.
06. ניתוח רגרסיה לאסו
לאסו (Least Absolute Shrinkage and Selection Operator) דומה לרגרסיה של רכס; עם זאת, הוא משתמש בהטיית ערך מוחלטת במקום בהטיה הריבועית המשמשת ברגרסיה של רכס.
הוא פותח כבר בשנת 1989 כחלופה לאומדן הריבועים הפחות מסורתיים מתוך כוונה להסיק את רוב הבעיות הקשורות להתאמת יתר כאשר לנתונים יש מספר רב של משתנים בלתי תלויים.
לאסו יש את היכולת לבצע את שניהם – בחירת משתנים והסדרתם יחד עם סף רך. יישום רגרסיה לאסו מקל על הפקת תת-קבוצה של מנבאים ממזעור טעויות ניבוי תוך ניתוח תגובה כמותית.
שים לב שמקדמי רגרסיה המגיעים לערך אפס לאחר התכווצות אינם נכללים במודל לאסו. להיפך, מקדמי רגרסיה בעלי ערך רב מאפס קשורים מאוד למשתני התגובה, כאשר המשתנים המסבירים יכולים להיות כמותיים, קטגוריים או שניהם.
דוגמה
נניח שחברת רכב רוצה לבצע ניתוח מחקרי על צריכת הדלק הממוצעת של מכוניות בארה"ב. עבור דוגמאות, הם בחרו 32 דגמים של מכונית ו -10 תכונות של עיצוב רכב – מספר צילינדרים, תזוזה, כוח סוס ברוטו, יחס סרן אחורי, משקל, 1/4 קילומטר זמן, מנוע v/s, תיבת הילוכים, מספר הילוכים, ומספר קרבורטורים.
כפי שניתן לראות, מתאם בין משתנה התגובה mpg (מיילים לגלון) מתואם מאוד עם כמה משתנים כמו משקל, תזוזה, מספר צילינדרים וכוחות סוס. ניתן לנתח את הבעיה באמצעות חבילת glmnet ברגרסיה R ולאסו לבחירת תכונות.
07. ניתוח רגרסיה אלסטית נטו
זוהי תערובת של מודלים של רגרסיה רכס לאסו מאומנים עם נורמות L1 ו- L2. הרשת האלסטית יוצרת אפקט קיבוץ שבו מנבאים בעלי מתאם חזק נוטים להיות בתוך/יציאה מהמודל יחד. שימוש במודל רגרסיה נטו אלסטית מומלץ כאשר מספר המנבאים גדול בהרבה ממספר התצפיות.
יש לציין כי מודל רגרסיה נטו אלסטית בא לעולם כאופציה למודל רגרסיה לאסו מכיוון שקטע המשתנה של לאסו היה תלוי מדי בנתונים, מה שהפך אותו ללא יציב. על ידי שימוש ברגרסיה אלסטית נטו, סטטיסטיקאים הפכו למסוגלים לגשר יתר על המידה על העונשים של רגרסיה רכס ולאסו רק כדי להפיק את המיטב משני המודלים.
דוגמה
צוות מחקר קליני בעל גישה למערך נתונים של מיקרו-מערך על לוקמיה (LEU) היה מעוניין לבנות כלל אבחון המבוסס על רמת הביטוי של דגימות הגן המוצגות לחיזוי סוג הלוקמיה. מערך הנתונים שהיה ברשותם כלל מספר רב של גנים וכמה דגימות.
מלבד זאת, הם קיבלו קבוצה ספציפית של דגימות שישמשו כדגימות אימון, מתוכן חלקן נדבקו בלוקמיה מסוג 1 (לוקמיה לימפובלסטית חריפה) וחלקן בלוקמיה מסוג 2 (לוקמיה מיאלואידית חריפה).
התאמת המודל ובחירת פרמטר כוונון לפי פי עשרה קורות חיים בוצעו על נתוני האימון. לאחר מכן הם השוו את הביצועים של שיטות אלה על ידי חישוב ממוצע החיזוי שלהם שגיאה בריבוע על נתוני הבדיקה כדי לקבל את התוצאות הדרושות.
שימוש בניתוח רגרסיה במחקר שוק
סקר שוק מתמקד בשלוש מטריצות עיקריות; שביעות רצון לקוחות, נאמנות לקוחות וסנגור לקוחות. זכור, למרות שמטריצות אלה מספרות לנו על בריאות הלקוח וכוונותיו, הן אינן מספרות לנו דרכים לשיפור המיקום. לכן, שאלון סקר מעמיק שנועד לשאול את הצרכנים את הסיבה לחוסר שביעות הרצון שלהם הוא בהחלט דרך להגיע לתובנות מעשיות.
עם זאת, נמצא כי אנשים לעתים קרובות נאבקים להציג את המוטיבציה שלהם או demotivation או לתאר את שביעות הרצון או חוסר שביעות הרצון שלהם. בנוסף לכך, אנשים תמיד נותנים חשיבות מופרזת לכמה גורמים רציונליים, כגון מחיר, אריזה וכו '. בסך הכל, הוא פועל ככלי ניתוח חיזוי וחיזוי במחקר שוק.
כאשר משתמשים בו ככלי חיזוי, ניתוח רגרסיה יכול לקבוע את נתוני המכירות של הארגון על ידי התחשבות בנתוני שוק חיצוניים. חברה רב לאומית עורכת סקר שוק כדי להבין את ההשפעה של גורמים שונים כגון תמ"ג (תוצר מקומי גולמי), מדד המחירים לצרכן וגורמים דומים אחרים על מודל ייצור ההכנסות שלה.
כמובן, ניתוח רגרסיה בהתחשב באינדיקטורים שיווקיים חזויים שימש לחיזוי הכנסות טנטטיביות שייווצרו ברבעונים עתידיים ואפילו בשנים הבאות. עם זאת, ככל שתלך קדימה בעתיד, הנתונים יהפכו לבלתי אמינים יותר, וישאירו מרווח טעות רחב.
מקרה בוחן של שימוש בניתוח רגרסיה
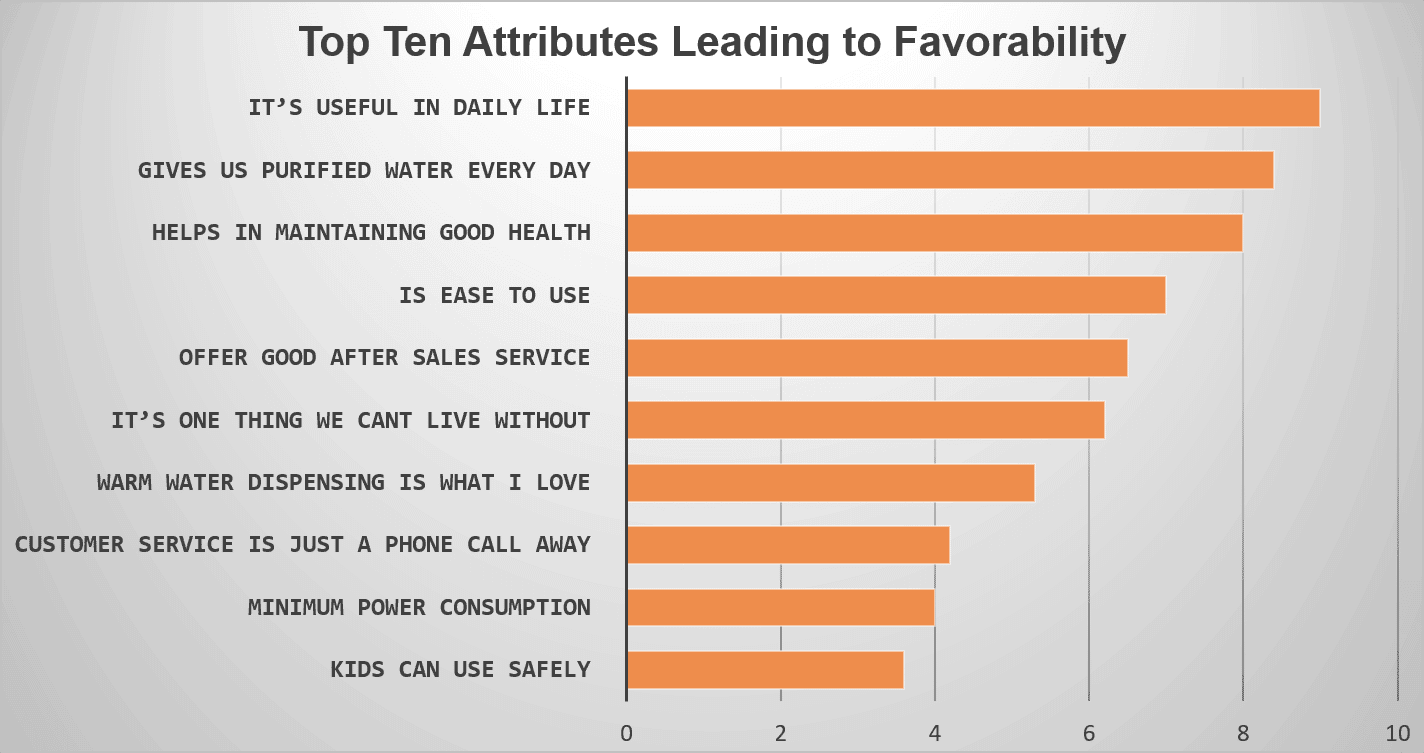
חברת מטהרי מים רצתה להבין את הגורמים המובילים להעדפת המותג. הסקר היה המדיום הטוב ביותר להגיע ללקוחות קיימים ופוטנציאליים. תוכנן סקר צרכנים רחב היקף, והוכן שאלון דיסקרטי באמצעות כלי הסקר הטוב ביותר.
מספר שאלות הקשורות למותג, העדפה, שביעות רצון וחוסר שביעות רצון סביר נשאלו ביעילות בסקר. לאחר קבלת תשובות אופטימליות לסקר, ניתוח רגרסיה שימש כדי לצמצם את עשרת הגורמים המובילים האחראים להנעת העדפת המותג.
כל עשר התכונות הנגזרות (המוזכרות בתמונה למטה) בדרך זו או אחרת הדגישו את חשיבותן בהשפעה על ההעדפה של אותו מותג מטהר מים ספציפי.
כיצד ניתוח רגרסיה מפיק תובנות מסקרים?
קל להריץ ניתוח רגרסיה באמצעות Excel או SPSS, אך תוך כדי כך, יש להבין את חשיבותם של ארבעה מספרים בפענוח הנתונים.
שני המספרים הראשונים מתוך ארבעת המספרים מתייחסים ישירות למודל הרגרסיה עצמו.
- ערך F: זה עוזר למדוד את המובהקות הסטטיסטית של מודל הסקר. זכרו, ערך F נמוך משמעותית מ-0.05 נחשב למשמעותי יותר. פחות מ- 0.05 F-Value מבטיח שפלט ניתוח הסקר אינו מקרי.
- R-בריבוע: זהו הערך שבו המשתנים הבלתי תלויים מנסים להסביר את כמות התנועה על ידי משתנים תלויים. בהתחשב בכך שערך R-Squared הוא 0.7, משתנה בלתי תלוי נבדק יכול להסביר 70% מתנועת המשתנה התלוי. משמעות הדבר היא שפלט ניתוח הסקר שנקבל הוא בעל אופי ניבוי גבוה ויכול להיחשב מדויק.
שני המספרים האחרים מתייחסים לכל אחד מהמשתנים הבלתי תלויים תוך פירוש ניתוח רגרסיה.
- ערך P: כמו F-Value, אפילו P-Value הוא מובהק סטטיסטית. יתר על כן, כאן הוא מציין עד כמה רלוונטית ומובהקת סטטיסטית השפעת המשתנה הבלתי תלוי. שוב, אנו מחפשים ערך של פחות מ 0.05.
- פרשנות: המספר הרביעי מתייחס למקדם שהושג לאחר מדידת השפעת המשתנים. לדוגמה, אנו בודקים משתנים בלתי תלויים מרובים כדי לקבל מקדם. הוא אומר לנו, "באיזה ערך המשתנה התלוי צפוי לגדול כאשר משתנים בלתי תלויים (שאנו שוקלים) גדלים באחד כאשר כל שאר המשתנים הבלתי תלויים עומדים באותו ערך.
במקרים מעטים, המקדם הפשוט מוחלף במקדם סטנדרטי המדגים את תרומתו של כל משתנה בלתי תלוי להזיז או להביא לשינוי במשתנה התלוי.
יתרונות השימוש בניתוח רגרסיה בסקר מקוון
01. קבל גישה לניתוח תחזיתי
האם אתה יודע ששימוש בניתוח רגרסיה כדי להבין את התוצאה של סקר עסקי הוא כמו שיש לך את הכוח לחשוף הזדמנויות וסיכונים עתידיים?
לדוגמה, לאחר שראינו משבצת מסוימת של פרסומת בטלוויזיה, אנו יכולים לחזות את המספר המדויק של עסקים המשתמשים בנתונים אלה כדי להעריך את הצעת המחיר המרבית עבור משבצת זו. תעשיית הפיננסים והביטוח בכללותה תלויה רבות בניתוח רגרסיה של נתוני סקר כדי לזהות מגמות והזדמנויות לתכנון וקבלת החלטות מדויקים יותר.
02. שפר את היעילות התפעולית
האם אתה יודע שעסקים משתמשים בניתוח רגרסיה כדי לייעל את התהליכים העסקיים שלהם?
לדוגמה, לפני השקת קו מוצרים חדש, עסקים עורכים סקרי צרכנים כדי להבין טוב יותר את ההשפעה של גורמים שונים על הייצור, האריזה, ההפצה והצריכה של המוצר.
ראיית הנולד המבוססת על נתונים עוזרת לסלק את הניחושים, ההשערות והפוליטיקה הפנימית מקבלת ההחלטות. הבנה מעמיקה יותר של התחומים המשפיעים על יעילות תפעולית והכנסות מובילה לאופטימיזציה עסקית טובה יותר.
03. תמיכה כמותית בקבלת החלטות
סקרים עסקיים כיום מייצרים נתונים רבים הקשורים לכספים, הכנסות, תפעול, רכישות וכו', ובעלי עסקים תלויים מאוד במודלים שונים של ניתוח נתונים לקבלת החלטות עסקיות מושכלות.
לדוגמה, ניתוח רגרסיה מסייע לארגונים לקבל החלטות מושכלות לגבי כוח העבודה האסטרטגי. ביצוע ופירוש התוצאות של סקרי עובדים כמו סקרי מעורבות עובדים, סקרי שביעות רצון עובדים, סקרי שיפור מעסיקים, סקרי יציאת עובדים וכו ', מגביר את הבנת הקשר בין העובדים לארגון.
זה גם עוזר לקבל מושג הוגן על נושאים מסוימים המשפיעים על תרבות העבודה של הארגון, סביבת העבודה והפרודוקטיביות. יתר על כן, פרשנויות חכמות ומכוונות עסקים מצמצמות את הערימה העצומה של נתונים גולמיים למידע מעשי כדי לקבל החלטה מושכלת יותר.
04. למנוע טעויות לקרות עקב אינטואיציות
על ידי לדעת כיצד להשתמש בניתוח רגרסיה לפירוש תוצאות סקר, ניתן בקלות לספק תמיכה עובדתית להנהלה לקבלת החלטות מושכלות. ; אבל האם אתה יודע שזה גם עוזר למנוע פגמים בפסק הדין?
לדוגמה, מנהל קניון חושב שאם הוא יאריך את זמן הסגירה של הקניון, אז זה יביא ליותר מכירות. ניתוח רגרסיה סותר את האמונה כי חיזוי גידול בהכנסות עקב גידול במכירות לא יתמוך בהוצאות התפעוליות הגדלות הנובעות משעות עבודה ארוכות יותר.
מסקנה
ניתוח רגרסיה הוא שיטה סטטיסטית שימושית למידול והבנת היחסים בין משתנים. הוא מספק יתרונות רבים לסוגי נתונים ואינטראקציות שונות. חוקרים ואנליסטים עשויים לקבל תובנות שימושיות לגבי הגורמים המשפיעים על משתנה תלוי ולהשתמש בתוצאות כדי לקבל החלטות מושכלות.
עם QuestionPro Research, אתה יכול לשפר את היעילות והדיוק של ניתוח רגרסיה על ידי ייעול תהליכי איסוף, ניתוח ודיווח נתונים. הממשק הידידותי למשתמש של הפלטפורמה ומגוון רחב של תכונות הופכים אותה לכלי רב ערך עבור חוקרים ואנליסטים המבצעים ניתוח רגרסיה כחלק מפרויקטי המחקר שלהם.
הירשם לניסיון בחינם עוד היום ותן לחלומות המחקר שלך לעוף!







