מקדם מתאם פירסון: הגדרה, נוסחה וחישוב, ודוגמאות

מקובל לכמת יחסים ליניאריים באמצעות מקדם המתאם של פירסון. כדי לציין את החוזק והכיוון של הקשר בין שני משתנים, הוא מקבל ערך בין -1 ל- 1.

זה יכול לעזור למשקיעים לגוון. חישובים מתוך חלקות פיזור של תשואות היסטוריות בין זוגות נכסים, כגון מניות-אג"ח, מניות-סחורות, אג"ח-נדל"ן וכו', יפיקו כדי לסייע למשקיעים לבנות תיקי תשואה-סיכון.

לכן, נלמד על מקדם המתאם פירסון ונדע למדוד באמצעותו את הקשר בין שני משתנים קשורים.

מהו מקדם המתאם של פירסון?

מקדם המתאם של פירסון או מקדם המתאם של פירסון או r של פירסון מוגדר בסטטיסטיקה כמדידת עוצמת הקשר בין שני משתנים והקשר שלהם זה לזה.

במילים פשוטות, מקדם המתאם של פירסון מחשב את השפעת השינוי במשתנה אחד כאשר המשתנה השני משתנה.

לדוגמה: עד גיל מסוים (ברוב המקרים), גובהו של הילד ימשיך לעלות ככל שגילו יעלה. כמובן שהגדילה שלו תלויה בגורמים שונים כמו גנים, מיקום, תזונה, אורח חיים וכו'.

גישה זו מבוססת על שונות משותפת, ולכן היא השיטה הטובה ביותר למדוד את הקשר בין שני משתנים.

מה עושה מבחן מקדם המתאם של פירסון?

למתאם מקדם פירסון מובהקות סטטיסטית גבוהה. הוא בוחן את הקשר בין שני משתנים. הוא מבקש למתוח קו דרך הנתונים של שני משתנים כדי להראות את הקשר ביניהם. הקשר בין המשתנים נמדד בעזרת מחשבון מקדם המתאם של פירסון. קשר ליניארי זה יכול להיות חיובי או שלילי.

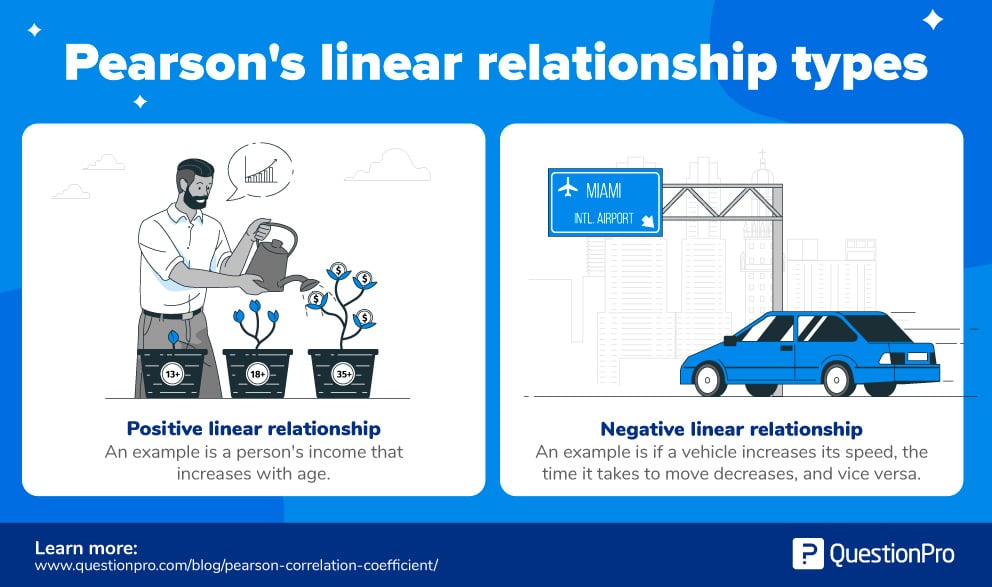
לדוגמה:

• קשר ליניארי חיובי: ברוב המקרים, באופן אוניברסלי, הכנסתו של אדם עולה ככל שגילו עולה.
• קשר ליניארי שלילי: אם הרכב מגביר את מהירותו, זמן הנסיעה פוחת, ולהיפך.

מהדוגמה לעיל, ניכר כי מקדם המתאם של פירסון, r, מנסה לברר שני דברים – חוזק וכיוון הקשר מגדלי המדגם הנתונים.

צור חשבון בחינם

נוסחת מקדם מתאם פירסון וחישוב

נוסחת מקדם המתאם מגלה את הקשר בין המשתנים. היא מחזירה את הערכים בין -1 ל- 1. השתמש במחשבון מתאם מקדם פירסון להלן כדי למדוד את חוזקם של שני משתנים.

נוסחת מקדם מתאם פירסון:

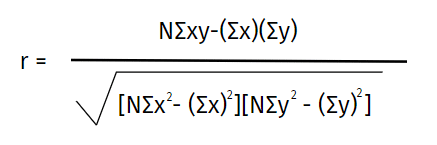
איפה:
N = מספר זוגות הציונים
Σxy = סכום המכפלות של ציונים זוגיים
Σx = סכום x ציונים
Σy = סכום הציונים
yΣ x 2 = סכום ציוני x בריבוע
Σy2 = סכום הציונים בריבוע y

חישוב

להלן מדריך שלב אחר שלב לחישוב מקדם המתאם של פירסון:

שלב ראשון: צור טבלת מקדמי מתאם.
צור תרשים נתונים, כולל שני המשתנים. תייג משתנים אלה 'x' ו- 'y'. הוסף שלוש עמודות נוספות – (xy), (x^2) ו- (y^2). עיין בטבלת נתונים פשוטה זו.

שלב שני: השתמש בכפל בסיסי כדי להשלים את הטבלה.

שלב שלישי: חבר את כל העמודות מלמטה למעלה.

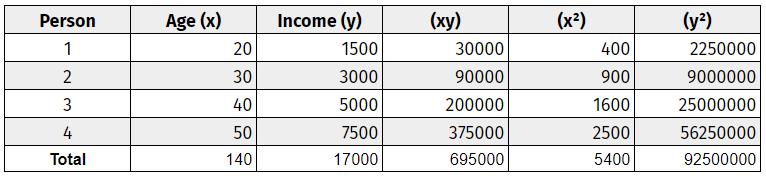
שלב רביעי: השתמש בנוסחת המתאם כדי לחבר את הערכים.

אם התוצאה שלילית, קיים קשר מתאם שלילי בין שני המשתנים. אם התוצאה חיובית, קיים קשר מתאם חיובי בין המשתנים. תוצאות יכולות גם להגדיר את חוזקו של קשר ליניארי, כלומר מערכת יחסים חיובית חזקה, מערכת יחסים שלילית חזקה, מערכת יחסים חיובית בינונית וכן הלאה.

קביעת חוזקו של מקדם המתאם בין מוצר למומנט של פירסון

מקדם המתאם מכפלה-מומנט של פירסון, או פשוט מקדם המתאם של פירסון או מקדם פירסון r, קובע את חוזק הקשר הליניארי בין שני משתנים.

ככל שהקשר בין שני המשתנים חזק יותר, כך התשובה שלך תיטה קרוב יותר לכיוון 1 או -1. השגת ערכים של 1 או -1 מסמלת שכל נקודות הנתונים משורטטות על הקו הישר של 'ההתאמה הטובה ביותר'. משמעות הדבר היא כי השינוי בגורמים של משתנה כלשהו אינו מחליש את המתאם עם המשתנה האחר. ככל שהתשובה קרובה יותר ל-0, כך גדלה השונות במשתנים.

כיצד לפרש את מקדם המתאם של פירסון

להלן הקווים המנחים המוצעים לפרשנות מתאם מקדם פירסון: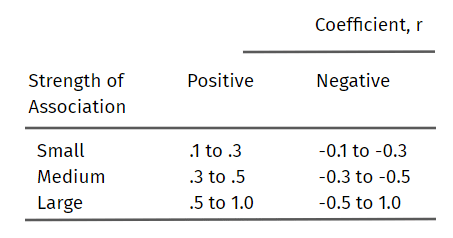

שים לב שעוצמת הקשר של המשתנים תלויה במה שאתה מודד ובגודל המדגם.

בגרף, ניתן להבחין בקשר בין המשתנים ולהניח הנחות עוד לפני חישובם. הפיזורים, אם הם קרובים לקו, מראים קשר חזק בין המשתנים.

ככל שחלקות הפיזור קרובות יותר לקו, כך הקשר בין המשתנים חזק יותר. ככל שהם מתרחקים מהקו, כך היחסים נחלשים. אם הקו כמעט מקביל לציר ה-x בשל הפיזורים הממוקמים באופן אקראי בגרף, סביר להניח שאין מתאם בין שני המשתנים.

מה משמעות המונחים כוח וכיוון?

למונחים 'כוח' ו'כיוון' יש מובהקות סטטיסטית. הנה הסבר פשוט לשתי המילים:

• חוזק: חוזק מסמל את מתאם היחסים בין שני משתנים. זה אומר כמה משתנה אחד ישתנה באופן עקבי עקב השינוי באחר. ערכים הקרובים ל- +1 או -1 מצביעים על קשר גומלין חזק. ערכים אלה מושגים אם נקודות הנתונים נופלות על הקו או קרובות מאוד אליו.
  
  ככל שנקודות הנתונים מתרחקות, כך עוצמת הקשר הליניארי נחלשת. כאשר אין דרך מעשית לצייר קו ישר מכיוון שנקודות הנתונים מפוזרות, חוזק הקשר הליניארי הוא החלש ביותר.
• כיוון: כיוון הקו מציין קשר ליניארי חיובי או ליניארי שלילי בין משתנים. אם לקו יש שיפוע כלפי מעלה, למשתנים יש קשר חיובי.
  
  משמעות הדבר היא שעלייה בערך של משתנה אחד תוביל לעלייה בערך של המשתנה השני. מתאם שלילי מתאר שיפוע כלפי מטה. משמעות הדבר היא שעלייה בכמות של משתנה אחד מובילה לירידה בערך של משתנה אחר.

צור חשבון בחינם

דוגמאות למקדם מתאם פירסון

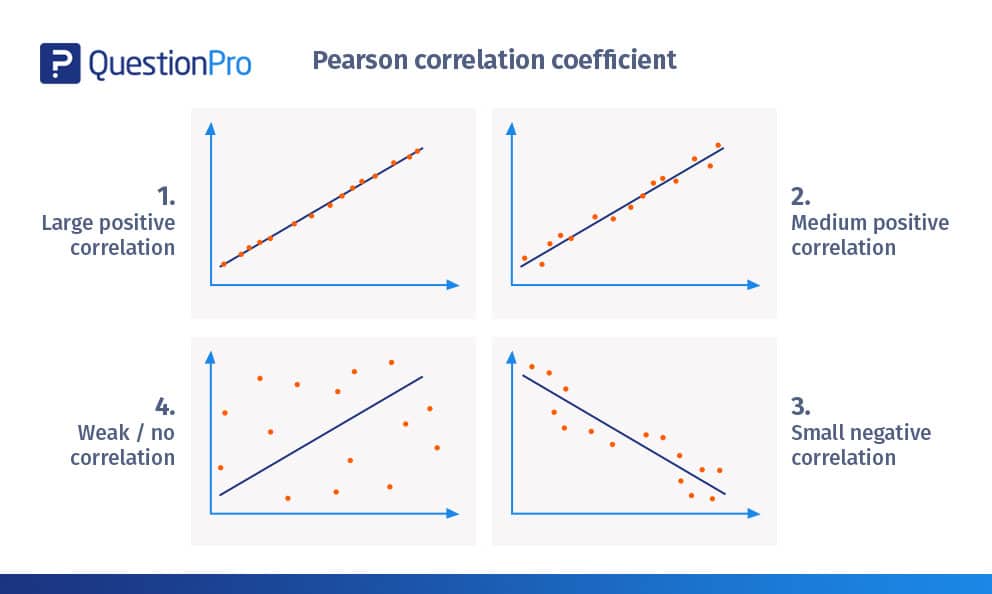
בואו נסתכל על כמה דוגמאות חזותיות שיעזרו לכם לפרש את טבלת מקדמי המתאם:

מתאם חיובי גדול

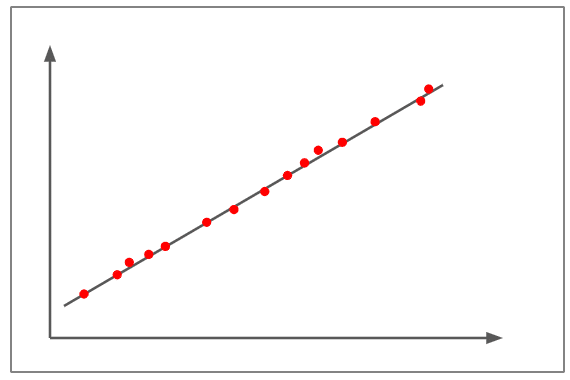
• האיור לעיל מתאר מתאם של כמעט +1.
• חלקות הפיזור כמעט משורטטות בקו ישר.
• השיפוע חיובי, כלומר אם משתנה אחד עולה, גם המשתנה השני עולה, ומראה קו ליניארי חיובי.
• זה מציין ששינוי במשתנה אחד עומד ביחס ישר לשינוי במשתנה השני.
• דוגמה למתאם חיובי גדול תהיה – ככל שילדים גדלים, כך גם מידות הבגדים והנעליים שלהם.

מתאם חיובי בינוני

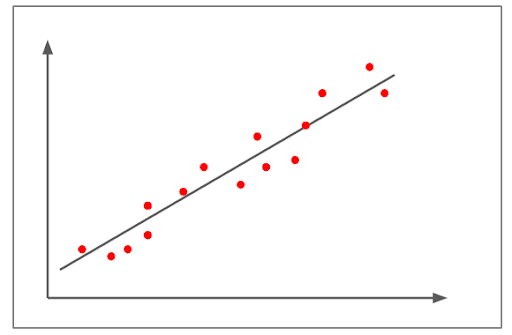
• האיור לעיל מתאר מתאם חיובי.
• המתאם הוא מעל +0.8 אך מתחת ל-1+.
• זה מראה דפוס ליניארי חזק למדי בעלייה.
• דוגמה למתאם חיובי בינוני תהיה – ככל שמספר המכוניות גדל, כך גדל הביקוש למשתנה הדלק.

מתאם שלילי קטן

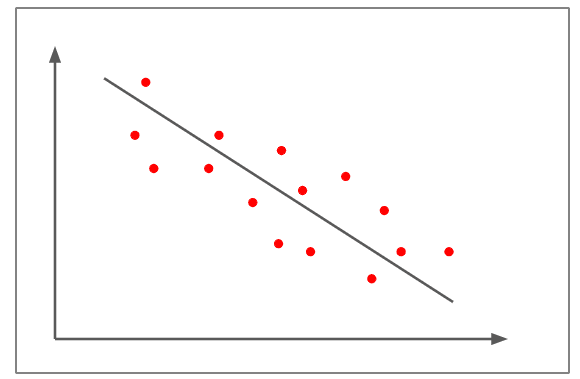
• באיור לעיל, חלקות הפיזור אינן קרובות לקו הישר בהשוואה לדוגמאות הקודמות
• זה מראה מתאם ליניארי שלילי של כ -0.5
• השינוי במשתנה אחד עומד ביחס הפוך לשינוי במשתנה השני, שכן השיפוע שלילי.
• דוגמה למתאם שלילי קטן תהיה – ככל שמישהו אוכל יותר, כך הוא נעשה פחות רעב.

חלש / ללא קורלציה

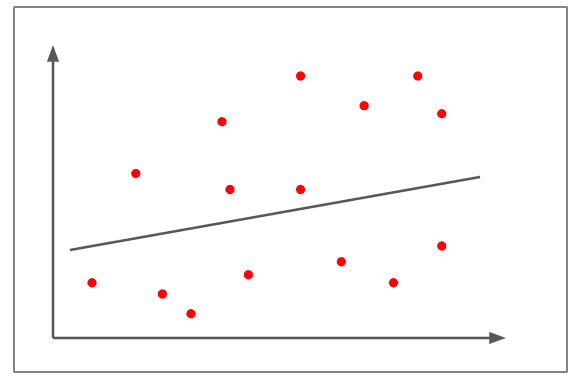
• חלקות הפיזור רחוקות מהקו.
• קשה למתוח קו באופן מעשי.
• המתאם הוא בערך +0.15
• לא ניתן לשפוט כי השינוי במשתנה אחד הוא ביחס ישר או ביחס הפוך למשתנה השני.
• דוגמה למתאם חלש/ללא קורלציה תהיה – עלייה במחירי הדלק מובילה לכך שפחות אנשים מאמצים חיות מחמד.

מסקנה

ניתן לקבוע את מקדם המתאם של פירסון על ידי איסוף נתונים על שני משתנים מעניינים באמצעות סקר. אתה יכול להשתמש בזה כדי ללמוד אם המתאם בין שני המשתנים הוא חיובי או שלילי וכמה חזק הוא.

QuestionPro Research Suite היא חבילת כלים למינוף המחקר ולשינוי תובנות שניתן להשתמש בהן כדי לאסוף נתונים עבור ניתוח מקדמי מתאם פירסון. לאחר ייצוא נתוני סקר מ- QuestionPro וייבואם לגיליון אלקטרוני או ליישום סטטיסטי, תוכל לבצע את ניתוח המתאם.

QuestionPro מציעה כלים מועילים לניתוח נתונים כגון הצלבות, ויזואליזציה של נתונים ובדיקות סטטיסטיות, בנוסף לחישוב מקדם המתאם. תכונות אלה יכולות לסייע במחקר שלך ובהבנת יחסי הגומלין של המשתנים שלך.

מוכנים לגלות את הקשר בין המשתנים שלכם ולקדם את ניתוח הנתונים שלכם? התחל ניסיון חינם של QuestionPro עוד היום כדי לראות כיצד תוכנת הסקרים שלנו יכולה לעזור לך לקבוע את מקדם המתאם של פירסון בקלות. אל תחמיצו הזדמנות זו לשפר את ניתוח הנתונים והמחקר.

ניסיון ללא תשלום מידע נוסף