
מתאם הוא מושג בסיסי בסטטיסטיקה ובניתוח נתונים, המסייע להבין את הקשר בין שני משתנים. בעוד מתאמים חיוביים או שליליים חזקים מודגשים לעתים קרובות, מתאם אפס חשוב באותה מידה.
זה אומר שאין קשר ליניארי בין המשתנים. במילים אחרות, שינויים במשתנה אחד אינם מנבאים שינויים באחר.
בבלוג זה נחקור את המושג מתאם אפס, ונספק הגדרה ברורה, דוגמאות להמחשה ושיטות לקבוע אותו.
מהו מתאם אפס?
מתאם אפס הוא מונח סטטיסטי המתאר מצב שבו אין קשר ליניארי בין שני משתנים. כאשר לשני משתנים יש מתאם אפס, שינויים במשתנה אחד אינם מנבאים שינויים בשני. מקדם המתאם, המודד את מידת וכיוון הקשר בין משתנים, הוא בדיוק אפס במקרה זה.
הבנת מתאם זה חשובה בניתוח סטטיסטי מכיוון שהיא מסייעת לזהות משתנים שאין להם קשר ניבוי זה עם זה, שהוא חיוני בעת בניית מודלים סטטיסטיים או פירוש דפוסי נתונים.
מדוע מתאם אפס חשוב?
מתאם אפס הוא מושג חשוב בסטטיסטיקה וניתוח נתונים מכמה סיבות כגון:
הוא מזהה עצמאות
זה עוזר לזהות משתנים שאינם תלויים ליניארית זה בזה. אם לשני משתנים יש מתאם אפס, שינויים במשתנה אחד אינם מספקים מידע על שינויים באחר. זה חיוני להבנת מבנה הנתונים והיחסים (או היעדרם) בין משתנים.
זה משפר מודלים סטטיסטיים
בניתוח רגרסיה ומודלים סטטיסטיים אחרים, כולל משתנים עם מתאם זה למשתנה התלוי יכולים להוסיף רעש ולהפחית את כוח הניבוי של המודל. על ידי זיהוי ואי הכללה של משתנים כאלה, ניתן לפשט מודלים ולהפוך אותם ליעילים יותר, מה שמוביל לביצועים טובים יותר וליכולת פרשנות טובים יותר.
מתאם זה מסייע למנוע פרשנות שגויה
הבנת מתאם זה מונעת פרשנות שגויה של נתונים.
- לדוגמה, חוקר עשוי להסיק בטעות קשר בין שני משתנים בהתבסס על אינטואיציה או תצפיות ראשוניות.
חישוב מקדם המתאם וקביעתו כאפס מבהיר כי לא קיים קשר ליניארי, תוך הימנעות ממסקנות שגויות.
הוא מדגיש יחסים לא ליניאריים
זה מדגיש את האפשרות של יחסים לא ליניאריים. אם לשני משתנים יש מתאם אפס, זה לא בהכרח אומר שהם לא קשורים; ייתכן שיש להם מערכת יחסים מורכבת ולא ליניארית. הכרה בכך יכולה להניע חקירה נוספת באמצעות שיטות אחרות, כגון רגרסיה לא ליניארית או המרות נתונים.
מתאם מסייע בהנחיית תכנון ניסויי
בתכנון ניסויי, הידיעה לאילו משתנים יש מתאם אפס יכולה להנחות את בחירת המשתנים שיש לכלול או לשלוט בהם. זה עוזר לתכנן ניסויים חזקים יותר שבהם ההשפעה של משתנים לא רלוונטיים ממוזערת, מה שמוביל לתוצאות ברורות ואמינות יותר.
הוא מבין התנהגות משתנה
הוא מספק תובנות לגבי ההתנהגות של משתנים בערכת נתונים. בניתוח פיננסי, הבנה לאילו נכסים יש מתאם אפסי זה עם זה יכולה לסייע בפיזור התיק, שכן שילוב נכסים כאלה יכול להפחית את הסיכון הכולל.
הוא תומך בבדיקת השערות
בבדיקת השערות, מתאם זה הוא לעתים קרובות השערת אפס.
- לדוגמה, בבדיקה אם שני משתנים קשורים, השערת האפס עשויה לקבוע שהמתאם ביניהם הוא אפס.
קביעה אם זה נכון או לא נכון מסייעת באימות או הפרכה של השערות.
מהן הדוגמאות למתאם אפס?
דוגמאות למתאם זה, שבו שינויים במשתנה אחד אינם תואמים לשינויים במשתנה אחר, ניתן למצוא בתחומים שונים כגון:
תחום מחקר
דוגמה: מספר פרסומים מדעיים וטעם גלידה אהוב
מחקר בוחן את הקשר בין מספר הפרסומים המדעיים שיש לחוקר לבין טעם הגלידה האהוב עליו.
אין קשר הגיוני בין מספר המאמרים המדעיים שחוקר מפרסם לבין העדפתו לטעם גלידה מסוים. כתוצאה מכך, שני משתנים אלה צפויים להציג מתאם זה.
תחום החינוך
דוגמה: מידת הנעליים של התלמידים והציונים שלהם במתמטיקה
מחקר חינוכי בודק האם יש קשר בין מידות הנעליים של התלמידים לבין ציוניהם במתמטיקה.
מידת נעליים היא מאפיין פיזי שאין לו השפעה על הביצועים האקדמיים של התלמיד במתמטיקה. לכן, המתאם בין מידת הנעליים לציונים במתמטיקה צפוי להיות אפס.
תחום הבריאות
דוגמה: סוג דם ושכיחות הצטננות
מחקר רפואי בודק אם יש קשר בין סוג הדם של אדם לבין מספר הפעמים שהם נדבקים בהצטננות בשנה.
סוג הדם אינו קשור לתדירות ההידבקות בהצטננות, המושפעת מגורמים שונים נוספים כגון חשיפה לנגיפים וחוזק מערכת החיסון. לפיכך, המתאם בין סוג הדם להיארעות ההצטננות צפוי להיות אפסי.
כיצד לזהות מתאם אפס?
כאן נחקור כיצד לזהות מתאם זה באמצעות בדיקה חזותית, חישוב סטטיסטי, בדיקת השערות וניתוח הקשרי.
1. ויזואליה של הבדיקה באמצעות חלקות פיזור
תרשימי פיזור הם כלי יעיל להערכה חזותית של הקשר בין שני משתנים.
יצירת תרשים פיזור:
- מקם משתנה אחד על ציר ה-x והשני על ציר ה-y.
- חפש כל מגמה או דפוס שניתן להבחין בהם בנקודות הנתונים.
זיהוי קורלציה:
- אם הנקודות מפוזרות באופן אקראי ללא מגמה ברורה (לא כלפי מעלה ולא כלפי מטה), הדבר מצביע על קורלציה.
- פיזור אקראי מרמז על כך שאף קו (ישר או עקום) אינו יכול להתאים היטב לנקודות הנתונים.
דוגמה:
- מידות נעליים של תלמידים לעומת ציונים במתמטיקה: אם אתה משרטט את מידות הנעליים מול ציוני מתמטיקה ורואה פיזור אקראי של נקודות ללא מגמה, זה מצביע על מתאם אפס.
2. חישוב מקדם המתאם
מקדם מתאם פירסון (r) הוא המדד הנפוץ ביותר למתאם ליניארי.
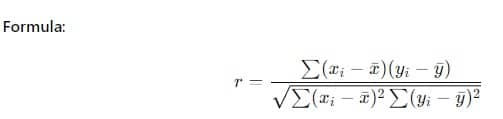
שלבים:
- אסוף נקודות נתונים מזוהות עבור שני המשתנים.
- מצא את הממוצע (ממוצע) של כל משתנה.
- חשב כמה רחוק כל נקודת נתונים מהממוצע.
- הכפל את הסטיות עבור כל זוג וסכם את המוצרים.
- השתמש בנוסחה כדי למצוא את מקדם המתאם.
פירוש קורלציה:
ערך קרוב ל-0: אם r r קרוב ל-0, הוא מציין קשר ליניארי מועט, אם בכלל, בין המשתנים.
דוגמה:
- מידות נעליים וציונים במתמטיקה: אם r המחושב הוא בערך 0, הוא מאשר מתאם אפס.
3. בצע את בדיקת ההשערה
בדיקת השערות סטטיסטיות יכולה לקבוע אם מקדם מתאם שנצפה שונה באופן משמעותי מאפס.
שלבים:
- השערת האפס: נניח שמקדם המתאם הוא אפס.
- השערה חלופית: נניח שמקדם המתאם אינו אפס.
- סטטיסטיקת מבחן חישוב: השתמש במבחן t עבור מקדם המתאם.
- קביעת ערך p: השווה את ערך ה-p לרמת מובהקות (לדוגמה, 0.05).
אפס קורלציה:
- אם ערך p גדול מרמת המובהקות, אל תדחה את השערת האפס, מה שמרמז על כך שהמתאם אינו שונה באופן משמעותי מאפס.
דוגמה:
- סוג דם ושכיחות הצטננות: בדיקת המתאם בין סוג הדם להיארעות הצטננות, אם ערך ה-p גבוה, מצביעה על כך שכל מתאם שנצפה אינו מובהק סטטיסטית, ותומך במתאם אפס.
4. הבנת ניתוח הקשרי
הבנת ההקשר והרקע התיאורטי של המשתנים חיונית לפירוש תוצאות המתאם.
שלבים:
- בחינת משתנים: שקול את האופי ואת היחסים הצפויים בין המשתנים.
- יישום ידע בתחום: השתמש בידע מהשטח כדי לשער אם מערכת יחסים צפויה.
אפס קורלציה:
- אם התיאוריה ומחקרים קודמים אינם מציעים קשר לוגי, הדבר תומך במציאת מתאם זה.
דוגמה:
- סוג דם ושכיחות הצטננות: הידיעה שסוג הדם אינו משפיע על הרגישות להצטננות תומכת בפענוח של מתאם אפס אם נמצא.
מתאם שלילי לעומת חיובי לעומת מתאם אפס
מתאם הוא מדד סטטיסטי המתאר את חוזקו וכיוונו של הקשר בין שני משתנים. הנה הסבר מפורט על מתאם שלילי, חיובי ואפס:
מתאם חיובי
- הגדרה: מתאם חיובי מתרחש כאשר שני משתנים נעים באותו כיוון. ככל שמשתנה אחד עולה, גם המשתנה השני עולה, וככל שאחד יורד, גם השני יורד.
- דוגמה: הקשר בין גובה למשקל. בדרך כלל, ככל שגובהו של אדם עולה, גם משקלם נוטה לעלות.
- ייצוג גרפי: בתרשים פיזור, נקודות נוטות להתקבץ סביב קו המשתפל כלפי מעלה משמאל לימין.
מתאם שלילי
- הגדרה: מתאם שלילי מתרחש כאשר שני משתנים נעים בכיוונים מנוגדים. ככל שמשתנה אחד עולה, המשתנה השני יורד, ולהיפך.
- דוגמה: הקשר בין משך הזמן המושקע בלמידה לבין מספר הטעויות שנעשו בבחינה. בדרך כלל, ככל שהזמן המושקע בלימוד גדל, מספר השגיאות פוחת.
- ייצוג גרפי: בחלקת פיזור, נקודות נוטות להתקבץ סביב קו המשתפל כלפי מטה משמאל לימין.
מתאם אפס
- הגדרה: זה מצביע על כך שאין קשר בין שני המשתנים. שינויים במשתנה אחד אינם מנבאים שינויים במשתנה השני.
- דוגמה: הקשר בין מידת הנעליים של אדם לבין מנת המשכל (IQ) שלו. אין קשר לוגי בין שני המשתנים הללו.
- ייצוג גרפי: בתרשים פיזור, נקודות מתפלגות באופן אקראי ללא תבנית או שיפוע ברורים.
כיצד QuestionPro יכולה לעזור בניתוח מתאמים?
QuestionPro, פלטפורמת סקרים חזקה, מציעה כלים מקיפים כדי להקל על ניתוח מתאם יעיל. הנה איך QuestionPro יכול לעזור לך בביצוע ניתוח מתאמים:
איסוף נתונים ללא מאמץ
QuestionPro מפשטת את תהליך איסוף הנתונים באמצעות כלי יצירת הסקרים הידידותיים למשתמש שלה. ניתן לעצב ולהפיץ סקרים לאיסוף נתונים כמותיים על משתנים שונים בעלי עניין. הפלטפורמה תומכת בסוגי שאלות שונים, ומאפשרת לך ללכוד נתונים מפורטים ורלוונטיים ביעילות.
ניתוח נתונים אוטומטי
לאחר איסוף הנתונים, QuestionPro מספקת כלי ניתוח מובנים לניתוח מתאמים. ניתן לחשב בקלות מתאמים, המודדים את החוזק והכיוון של הקשר הליניארי בין שני משתנים. מקדם המתאם הליניארי נע בין -1 ל-1, כאשר:
- 1 מצביע על מתאם חיובי מושלם.
- -1 מצביע על מתאם שלילי מושלם.
- 0 מציין שאין קורלציה.
ייצוג חזותי
QuestionPro מציעה כלי ויזואליזציה שיעזרו לך לפרש את תוצאות ניתוח המתאמים שלך. ניתן ליצור חלקות פיזור ומטריצות מתאם כדי לספק ייצוג גרפי ברור של היחסים בין משתנים. כלי עזר חזותי זה חיוני לזיהוי מהיר של מגמות ודפוסים.
זיהוי דפוסים ומגמות
באמצעות ניתוח המתאם של QuestionPro, החוקרים הבחינו בקורלציה (חיובית, שלילית או אפס) בין משתנים:
- מתאם חיובי: שני המשתנים נעים באותו כיוון. לדוגמה, הגדלת הוצאות הפרסום עשויה להיות בקורלציה עם מכירות מוגברות.
- מתאם שלילי: המשתנים נוטים לנוע בכיוונים מנוגדים. לדוגמה, זמן מסך מוגבר עשוי להיות בקורלציה עם ירידה בביצועים אקדמיים.
- אפס קורלציה: לא קיים קשר בין המשתנים. לדוגמה, מספר שנות הלימודים עשוי שלא להתאים למספר האותיות בשמו של אדם.
יישומים מעשיים
ניתוח מתאם ב QuestionPro יכול לשמש עבור יישומים מעשיים שונים, כגון:
- מחקר שוק: מדוד את האפקטיביות של קמפיינים שיווקיים על ידי מתאם בין הוצאות פרסום לביצועי מכירות.
- בריאות: להעריך את הקשר בין שימוש בתרופות לבין תוצאות המטופל, כגון רמות לחץ דם.
- חינוך: לקבוע את ההשפעה של הרגלי למידה על ביצועים אקדמיים על ידי מתאם שעות לימוד עם ציונים.
מסקנה
מתאם אפס בין שני משתנים מסמל היעדר קשר ליניארי, המצביע על כך ששינויים במשתנה אחד אינם תואמים לשינויים במשתנה אחר. על ידי חישוב מקדמי מתאם והצגה חזותית של נתונים באמצעות חלקות פיזור, חוקרים יכולים לקבוע במדויק אם משתנים מתואמים, מתואמים חיובית, מתואמים שלילית, או מראים מתאם זה.
השימוש ב- QuestionPro לניתוח מתאמים בסקרים שלך מספק דרך רבת עוצמה לחשוף קשרים משמעותיים בין משתנים. על ידי חקירת הממשק האינטואיטיבי של QuestionPro, כלי ניתוח מתקדמים ותכונות דיווח מקיפות, תוכל לבצע ניתוח מתאם ביעילות ולהפיק תובנות יקרות ערך מהנתונים שלך. צרו קשר עם QuestionPro עוד היום לקבלת מידע נוסף!







