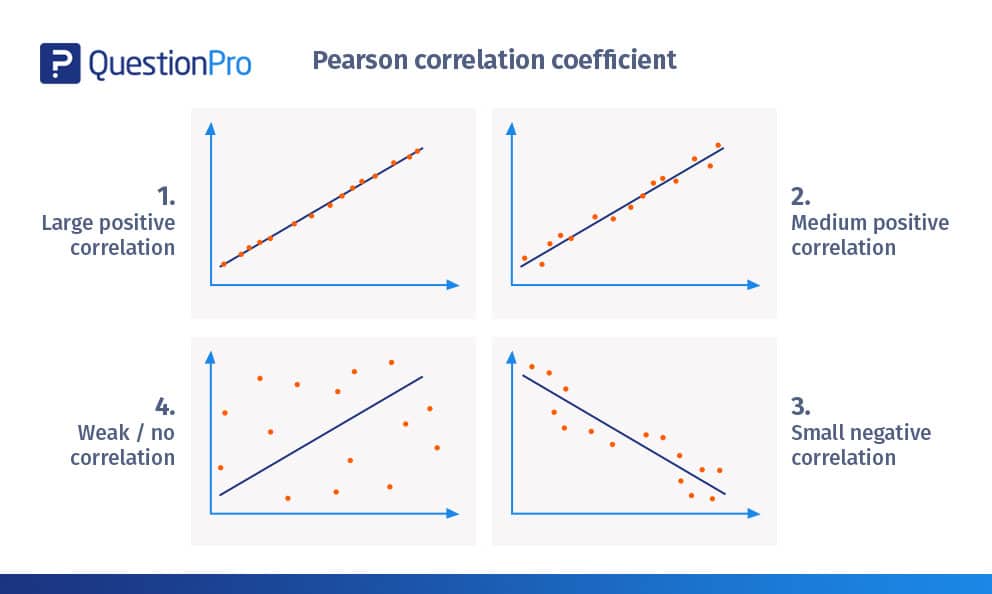
È consuetudine quantificare le relazioni lineari attraverso il coefficiente di correlazione di Pearson. Per indicare la forza e la direzione della connessione tra due variabili, assume un valore compreso tra -1 e 1.
Può aiutare gli investitori a diversificare. I calcoli dei diagrammi di dispersione dei rendimenti storici tra coppie di attività, come azioni-obbligazioni, azioni-materie prime, obbligazioni-immobili, ecc.
Pertanto, impareremo a conoscere il coefficiente di correlazione di Pearson e sapremo come misurare la relazione tra due variabili correlate.
Che cos’è il coefficiente di correlazione di Pearson?
Il coefficiente di correlazione di Pearson o coefficiente di correlazione di Pearson o r di Pearson è definito in statistica come la misura della forza della relazione tra due variabili e la loro associazione reciproca.
In parole povere, il coefficiente di correlazione di Pearson calcola l’effetto della variazione di una variabile al variare dell’altra.
Ad esempio: Fino a una certa età (nella maggior parte dei casi), l’altezza di un bambino continuerà a crescere con l’aumentare della sua età. Naturalmente, la sua crescita dipende da vari fattori come i geni, la posizione, la dieta, lo stile di vita, ecc.
Questo approccio si basa sulla covarianza ed è quindi il metodo migliore per misurare la relazione tra due variabili.
A cosa serve il test del coefficiente di correlazione di Pearson?
La correlazione del coefficiente di Pearson ha un’elevata significatività statistica. Esamina la relazione tra due variabili. Cerca di tracciare una linea attraverso i dati di due variabili per mostrare la loro relazione. La relazione tra le variabili viene misurata con l’aiuto del calcolatore del coefficiente di correlazione di Pearson. Questa relazione lineare può essere positiva o negativa.
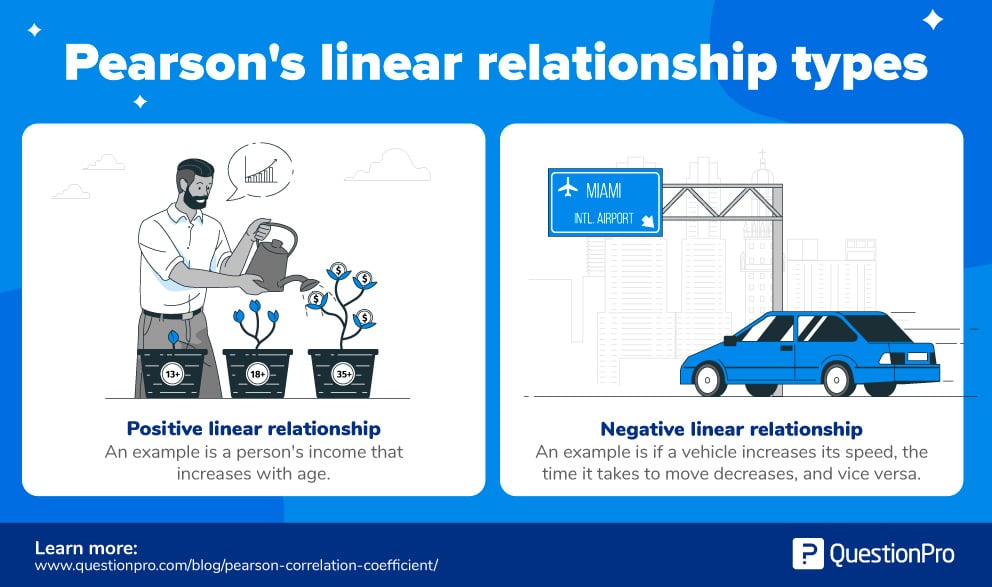
Ad esempio:
- Relazione lineare positiva: Nella maggior parte dei casi, universalmente, il reddito di una persona aumenta all’aumentare dell’età.
- Relazione lineare negativa: Se il veicolo aumenta la sua velocità, il tempo di percorrenza diminuisce e viceversa.
Dall’esempio precedente, è evidente che il coefficiente di correlazione di Pearson, r, cerca di scoprire due cose: la forza e la direzione della relazione a partire dalle dimensioni del campione.
Formula e calcolo del coefficiente di correlazione di Pearson
La formula del coefficiente di correlazione individua la relazione tra le variabili. Restituisce i valori compresi tra -1 e 1. Utilizzate il seguente calcolatore di correlazione del coefficiente di Pearson per misurare la forza di due variabili.
Formula del coefficiente di correlazione di Pearson:
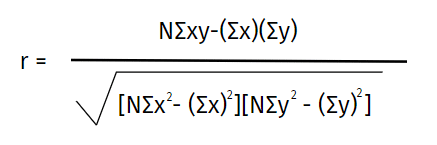
Dove:
N = il numero di coppie di punteggi
Σxy = la somma dei prodotti dei punteggi appaiati
Σx = la somma dei punteggi di x
Σy = la somma dei punteggi y
Σx2 = la somma dei punteggi al quadrato di x
Σy2 = la somma dei punteggi y al quadrato
Calcolo
Ecco una guida passo passo al calcolo del coefficiente di correlazione di Pearson:
Primo passo: Creare una tabella dei coefficienti di correlazione.
Creare un grafico dei dati, includendo entrambe le variabili. Etichettare queste variabili “x” e “y”. Aggiungere tre colonne supplementari: (xy), (x^2) e (y^2). Fate riferimento a questo semplice grafico di dati.

Secondo passo: Usare la moltiplicazione di base per completare la tabella.

Terzo passo: Sommare tutte le colonne dal basso verso l’alto.
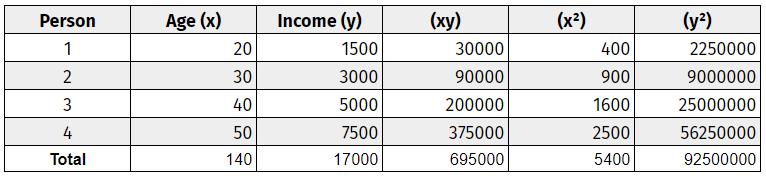
Quarto passo: Utilizzare la formula di correlazione per inserire i valori.
Se il risultato è negativo, esiste una relazione di correlazione negativa tra le due variabili. Se il risultato è positivo, esiste una relazione di correlazione positiva tra le variabili. I risultati possono anche definire la forza di una relazione lineare, cioè una forte relazione positiva, una forte relazione negativa, una media relazione positiva e così via.
Determinazione della forza del coefficiente di correlazione Pearson prodotto-momento
Il coefficiente di correlazione Pearson prodotto-momento, o semplicemente coefficiente di correlazione Pearson o coefficiente di correlazione Pearson r, determina la forza della relazione lineare tra due variabili.
Quanto più forte è l’associazione tra le due variabili, tanto più la risposta tenderà verso 1 o -1. Il raggiungimento di valori pari a 1 o -1 significa che tutti i punti dei dati sono tracciati sulla linea retta del “miglior adattamento”. Significa che la variazione dei fattori di una variabile non indebolisce la correlazione con l’altra variabile. Più la risposta è vicina allo 0, maggiore è la variazione delle variabili.
Come interpretare il coefficiente di correlazione di Pearson
Di seguito sono riportate le linee guida proposte per l’interpretazione della correlazione del coefficiente di Pearson: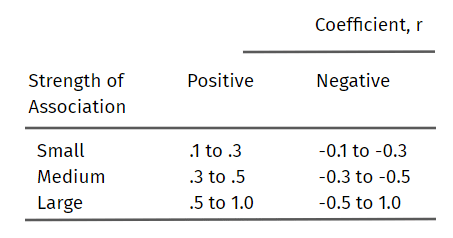
Si noti che la forza dell’associazione delle variabili dipende da ciò che si misura e dalle dimensioni del campione.
Su un grafico si può notare la relazione tra le variabili e fare ipotesi prima ancora di calcolarle. I diagrammi di dispersione, se vicini alla linea, mostrano una forte relazione tra le variabili.
Più i diagrammi di dispersione sono vicini alla linea, più forte è la relazione tra le variabili. Più si allontanano dalla linea, più la relazione si indebolisce. Se la linea è quasi parallela all’asse delle ascisse grazie ai diagrammi di dispersione posizionati in modo casuale sul grafico, è lecito supporre che non vi sia correlazione tra le due variabili.
Cosa significano i termini forza e direzione?
I termini “forza” e “direzione” hanno significato statistico. Ecco una spiegazione diretta delle due parole:
- Forza: La forza indica la correlazione tra due variabili. Significa quanto costantemente una variabile cambierà a causa della variazione dell’altra. Valori prossimi a +1 o -1 indicano una relazione forte. Questi valori vengono raggiunti se i punti dei dati cadono sulla linea o sono molto vicini ad essa.
Più i punti dati si allontanano, più la forza della relazione lineare si indebolisce. Quando non è possibile tracciare una linea retta perché i punti dei dati sono sparsi, la forza della relazione lineare è la più debole. - Direzione: La direzione della linea indica una relazione lineare positiva o negativa tra le variabili. Se la linea ha un’inclinazione verso l’alto, le variabili hanno una relazione positiva.
Ciò significa che un aumento del valore di una variabile porterà a un aumento del valore dell’altra variabile. Una correlazione negativa indica una pendenza verso il basso. Ciò significa che un aumento della quantità di una variabile porta a una diminuzione del valore di un’altra variabile.
Esempi di coefficiente di correlazione di Pearson
Vediamo alcuni esempi visivi per aiutarvi a interpretare la tabella dei coefficienti di correlazione:
Ampia correlazione positiva
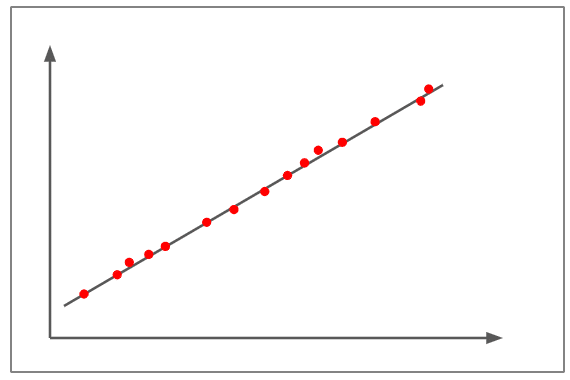
- La figura sopra riportata mostra una correlazione di quasi +1.
- I diagrammi di dispersione sono quasi tracciati in linea retta.
- La pendenza è positiva, il che significa che se una variabile aumenta, anche l’altra aumenta, mostrando una linea lineare positiva.
- Ciò significa che la variazione di una variabile è direttamente proporzionale alla variazione dell’altra variabile.
- Un esempio di grande correlazione positiva è il seguente: “Quando i bambini crescono, crescono anche i loro vestiti e le loro scarpe.
Correlazione mediamente positiva
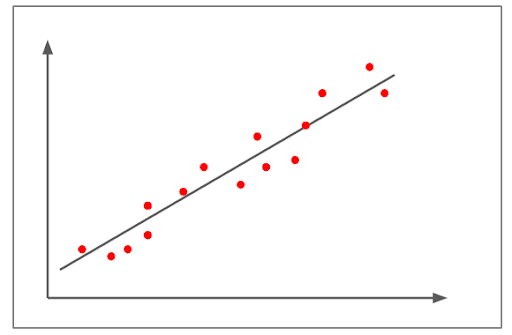
- La figura precedente mostra una correlazione positiva.
- La correlazione è superiore a +0,8 ma inferiore a 1+.
- Mostra un andamento lineare in salita piuttosto marcato.
- Un esempio di correlazione mediamente positiva potrebbe essere: con l’aumento del numero di automobili, aumenta anche la domanda della variabile carburante.
Piccola correlazione negativa
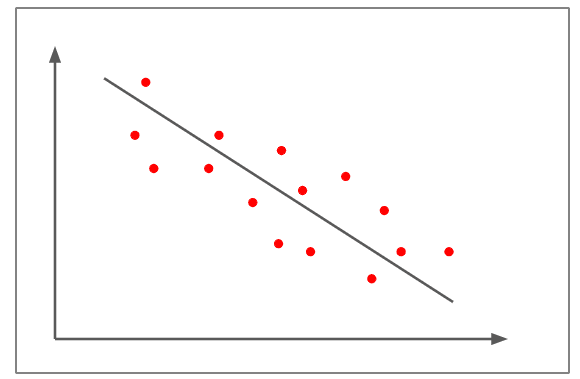
- Nella figura precedente, i diagrammi di dispersione non sono così vicini alla linea retta rispetto agli esempi precedenti.
- Mostra una correlazione lineare negativa pari a circa -0,5
- La variazione di una variabile è inversamente proporzionale alla variazione dell’altra variabile, poiché la pendenza è negativa.
- Un esempio di una piccola correlazione negativa potrebbe essere: più una persona mangia, meno ha fame.
Correlazione debole/assente
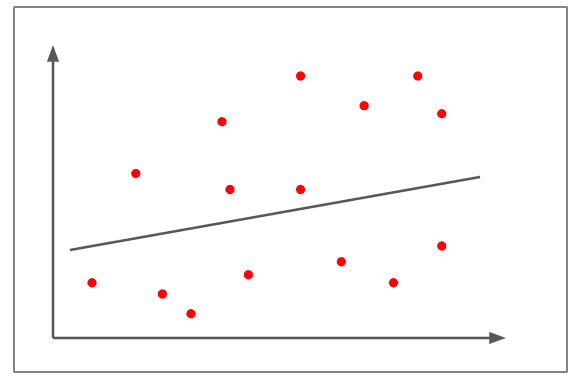
- I diagrammi di dispersione sono molto lontani dalla linea.
- È difficile tracciare una linea di demarcazione in pratica.
- La correlazione è di circa +0,15
- Non si può giudicare che la variazione di una variabile sia direttamente proporzionale o inversamente proporzionale all’altra variabile.
- Un esempio di correlazione debole/assente potrebbe essere: un aumento del prezzo del carburante porta a un minor numero di persone che adottano animali domestici.
Conclusione
Il coefficiente di correlazione di Pearson può essere determinato raccogliendo dati su due variabili di interesse attraverso un sondaggio. Si può usare per capire se la correlazione tra le due variabili è positiva o negativa e quanto è forte.
QuestionPro Research Suite è una suite di strumenti per sfruttare la ricerca e trasformare le intuizioni che possono essere utilizzate per raccogliere dati per l’analisi del coefficiente di correlazione di Pearson. Dopo aver esportato i dati dell’indagine da QuestionPro e averli importati in un foglio di calcolo o in un’applicazione statistica, è possibile condurre l’analisi di correlazione.
QuestionPro offre utili strumenti di analisi dei dati, come tabulazioni incrociate, visualizzazione dei dati e test statistici, oltre al calcolo del coefficiente di correlazione. Queste qualità possono aiutare nella ricerca e nella comprensione delle interrelazioni tra le variabili.
Siete pronti a scoprire la relazione tra le vostre variabili e ad avanzare nell’analisi dei dati? Iniziate oggi stesso una prova gratuita di QuestionPro per vedere come il nostro software per sondaggi può aiutarvi a determinare facilmente il coefficiente di correlazione di Pearson. Non perdete questa occasione per migliorare l’analisi dei dati e la ricerca.



