
Il test ANOVA o analisi della varianza è un metodo statistico che permette di scoprire se i risultati di un test sono significativi, cioè di determinare se è necessario rifiutare l’ipotesi nulla o accettare l’ipotesi alternativa.
Scopriamo le loro caratteristiche e i loro usi.
Cos’è l’analisi della varianza (ANOVA)?
L’analisi della varianza (ANOVA) è una tecnica statistica utilizzata per confrontare le medie di tre o più gruppi e determinare se ci sono differenze significative tra di essi. In altre parole, l’ANOVA ti aiuta a scoprire se esiste una differenza significativa nelle medie dei gruppi che stai confrontando o se le differenze che hai osservato sono semplicemente dovute al caso.
L’ANOVA confronta la varianza tra i gruppi con la varianza all’interno del gruppo. Se la varianza tra i gruppi è maggiore della varianza all’interno del gruppo, è probabile che ci sia una differenza significativa tra le medie. Se la varianza all’interno del gruppo è maggiore della varianza tra i gruppi, allora qualsiasi differenza osservata nelle medie potrebbe essere semplicemente casuale.
Esempio di ANOVA
Un semplice esempio di ANOVA o analisi della varianza potrebbe essere:
Immagina di avere tre insegnanti diversi (l’insegnante A, l’insegnante B e l’insegnante C) e di voler determinare se c’è una differenza significativa nei voti medi degli studenti nelle loro rispettive classi. Hai un gruppo di studenti e hai registrato i voti di ogni studente in ogni classe.
L’ANOVA ti aiuterà a rispondere alla domanda se esiste una differenza significativa nella media dei voti tra le classi di questi tre insegnanti. Ecco come si svolge:
- Ipotesi nulla (H0): non c’è alcuna differenza significativa nella media dei voti tra le classi dei tre insegnanti.
- Ipotesi alternativa (H1): Esiste una differenza significativa nella media dei voti tra almeno due classi di insegnanti.
In seguito, si raccoglieranno i dati e si eseguirà l’analisi della varianza. Se il valore p ottenuto dall’ANOVA è inferiore a un livello di significatività prestabilito (ad esempio 0,05), allora rifiuteremo l’ipotesi nulla e concluderemo che almeno due classi di insegnanti hanno voti medi significativamente diversi.
In breve, l’ANOVA è un test statistico utilizzato per confrontare più gruppi e determinare se ci sono differenze significative tra di essi. In questo esempio, è stato applicato al contesto dei voti degli studenti in tre classi di insegnanti diversi per verificare se le classi avessero prestazioni medie significativamente diverse.
Vantaggi dell’utilizzo del test ANOVA
Se stai raccogliendo dati metrici con i tuoi sondaggi, magari sotto forma di risposte a una scala scala Likert risposte a una scala Likert, l’importo speso per un prodotto, i punteggi di soddisfazione dei clienti o il numero di acquisti effettuati, puoi analizzare le differenze nel punteggio medio tra i gruppi di intervistati.
Se stai confrontando due gruppi alla volta (ad esempio uomini contro donne, nuovi clienti contro clienti esistenti, dipendenti contro manager, ecc.), è opportuno utilizzare il test t di Student per valutare la significatività delle differenze. Tuttavia, se i gruppi sono più di due, è necessario ricorrere a un’altra tecnica.
L’ANOVA o i suoi equivalenti non parametrici permettono di determinare se le differenze nei valori medi tra tre o più gruppi sono casuali o se sono significativamente diverse.
Questo metodo è particolarmente utile quando si analizzano le scale di più elementi comuni nelle ricerche di mercato.
L’ANOVA utilizza il test F per determinare se la variazione nelle risposte alle domande sulla soddisfazione è abbastanza grande da essere considerata statisticamente significativa.
I dati di per sé sono solo questo. Tuttavia, quando utilizziamo con giudizio i test statistici, possiamo creare delle intuizioni che possono avere un impatto positivo sui nostri sforzi di marketing.
L’uso corretto dell’ANOVA per analizzare i dati di un sondaggio richiede il rispetto di alcuni presupposti, tra cui la distribuzione normale dei dati, l’indipendenza dei casi e l’uguaglianza della varianza (la varianza di ciascun gruppo è uguale). Se questi presupposti non possono essere soddisfatti, allora ci sono test non parametrici disponibili che non richiedono questi presupposti.
A cosa serve l’Analisi della Varianza (ANOVA)?
L’analisi della varianza (ANOVA) è una tecnica statistica molto versatile e viene utilizzata in un’ampia varietà di campi. Alcuni dei principali utilizzi dell’ANOVA sono:
- Confronto delle medie: L’ANOVA viene utilizzata per confrontare le medie di tre o più gruppi per determinare se ci sono differenze significative tra di essi.
- Esperimenti controllati: Utilizzati negli esperimenti controllati per analizzare gli effetti di diversi trattamenti o interventi sui risultati.
- Ricerca di mercato: Utilizzato in ricerca di mercato per analizzare le preferenze dei consumatori per diversi prodotti o servizi.
- Scienze sociali: Analizzare la relazione tra diverse variabili, come l’età, l’istruzione e il reddito.
- Ricerca medica: L’ANOVA viene utilizzata nella ricerca medica per analizzare gli effetti di diversi trattamenti su pazienti affetti da una determinata malattia.
Scienze ambientali: analizzare gli effetti di diverse variabili sull’ambiente, come l’inquinamento e il clima.
Tipi di test ANOVA
I tre tipi di test ANOVA che possono essere eseguiti sono i seguenti:
ANOVA a una via: Ha una sola variabile indipendente. Questo metodo viene utilizzato per confrontare due medie di due gruppi indipendenti (non correlati) utilizzando la distribuzione F. L’ipotesi nulla del test è che le due medie siano uguali. Pertanto, un risultato significativo è che le due medie non sono uguali.
ANOVA a due vie: Questo metodo è un’estensione del test a una via. Tuttavia, il test ANOVA a due vie prevede due variabili indipendenti. In genere, viene utilizzato quando c’è una variabile di misura, cioè una variabile quantitativa e due variabili nominali.
MANOVA: Questo metodo viene utilizzato quando ci sono più variabili indipendenti. Il suo scopo è quello di determinare se la variabile dipendente cambia manipolando la variabile indipendente.
Le domande che MANOVA permette di risolvere sono le seguenti:
- I cambiamenti nelle variabili indipendenti hanno effetti statisticamente significativi sulle variabili dipendenti?
- Quali sono le interazioni tra le variabili dipendenti?
- Quali sono le interazioni tra le variabili indipendenti?
Come eseguire un’analisi della varianza con SPSS
Questi sono i passi da seguire per un’analisi della varianza con SPSS.
Passo 1: Clicca su “Analisi”, poi posiziona il cursore su “Modello lineare generale”. Clicca su “Misure ripetute”.
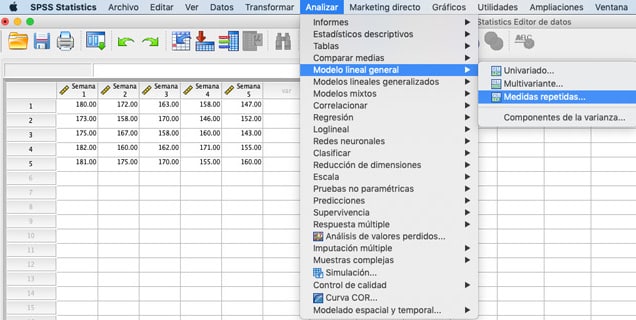
Passo 2: Sostituisci il nome “fattore1” con qualcosa che rappresenti la tua variabile indipendente.
Passo 3: Inserisci il “Numero di livelli”. Si tratta del numero di volte in cui la variabile dipendente è stata misurata.
Passo 4: Clicca sul pulsante “Aggiungi” e assegna un nome alla tua variabile dipendente.
Passo 5: Clicca sul pulsante “Aggiungi”. Apparirà un riquadro di definizione delle misure ripetute. Clicca sul pulsante “Definisci”.
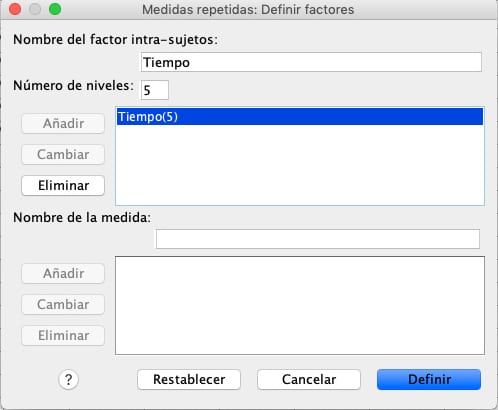
Passo 6: Sposta le variabili da destra a sinistra in modo che lo schermo assomigli all’immagine seguente:
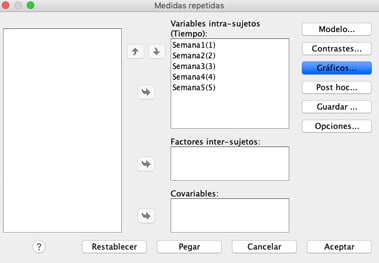
Passo 7: Clicca su “Grafici” e usa i tasti freccia per spostare il fattore dalla casella a sinistra a quella sull’asse orizzontale.
Passo 8: Clicca su “Aggiungi” e poi sul pulsante “Continua” in fondo alla finestra.
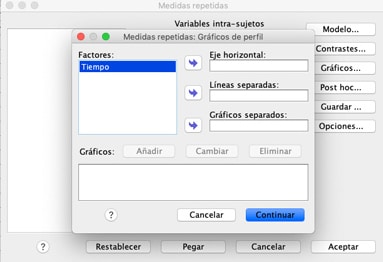
Passo 9: Clicca su “Opzioni” e trasferisci i tuoi fattori dalla casella a sinistra alla casella “Mostra medie” a destra.
Passo 10: Clicca sulle seguenti caselle di controllo:
- Confronta gli effetti principali
- Statistiche descrittive
- Stime della dimensione dell’effetto
Passo 11: Seleziona “Bonferroni” dal menu a tendina dell’opzione Impostazione dell’intervallo di confidenza.
Intervallo di confidenza.
Passo 12: Clicca su “Continua” e poi su “OK” per eseguire il test.
Differenza tra il test ANOVA e il test t di Student
La differenza principale tra il test ANOVA e il test t-test di Student Test t di Studentè che il test t di Student viene utilizzato per confrontare le medie di due gruppi, mentre il test ANOVA viene utilizzato per confrontare le medie di tre o più gruppi.
Il test t di Student è un test statistico parametrico utilizzato per confrontare le medie di due gruppi indipendenti. Viene utilizzato per determinare se esiste una differenza significativa tra le medie di due gruppi di dati. Il test t di Student si basa su un’ipotesi di normalità e di uguaglianza delle varianze nei due gruppi.
Il test ANOVA è invece un test statistico parametrico utilizzato per confrontare le medie di tre o più gruppi indipendenti. Viene utilizzato per determinare se esiste una differenza significativa tra le medie di tre o più gruppi di dati. Il test ANOVA si basa sul presupposto della normalità e dell’omogeneità delle varianze in tutti i gruppi.
Conclusione
In conclusione, l’analisi della varianza (ANOVA) è un potente strumento statistico utilizzato per confrontare le medie di tre o più gruppi di dati. Uno dei principali vantaggi dell’esecuzione di un test ANOVA è che permette di determinare se esiste una differenza significativa tra le medie dei gruppi, il che può essere utile in diversi ambiti come la ricerca scientifica, l’industria, il marketing e l’economia.
Nelle ricerche di mercato, il test ANOVA può essere utilizzato per confrontare le medie di diversi gruppi di consumatori, in base alle loro caratteristiche demografiche o comportamentali, e per valutare se ci sono differenze significative tra loro. Ad esempio, un test ANOVA può essere eseguito per confrontare le opinioni di diversi gruppi di consumatori su un prodotto, in base all’età, al sesso o al livello di istruzione.
Inoltre, l’ANOVA può essere utilizzata anche per valutare l’efficacia di diverse strategie di marketing. Ad esempio, un test ANOVA può essere eseguito per confrontare le vendite di un prodotto dopo l’applicazione di diverse strategie pubblicitarie o promozionali e per valutare se esiste una differenza significativa tra le vendite di ciascun gruppo.
Ricorda che QuestionPro può aiutarti nella tua prossima ricerca. Inizia subito a raccogliere i dati di cui hai bisogno!



