L’analisi di regressione è forse uno dei metodi statistici più utilizzati per studiare o stimare la relazione tra un insieme di variabili indipendenti e dipendenti. Nell’analisi statistica, la distinzione tra dati categorici e dati numerici è essenziale, poiché i dati categorici comportano categorie o etichette distinte, mentre i dati numerici consistono in quantità misurabili.
Viene anche utilizzato come termine generico per varie tecniche di analisi dei dati utilizzate in un metodo di ricerca qualitativo per modellare e analizzare numerose variabili. Nel metodo della regressione, la variabile dipendente è un fattore predittivo o un elemento esplicativo e la variabile dipendente è il risultato o la risposta a una domanda specifica.
IMPARARE SU: Metodi di analisi statistica
Definizione di analisi di regressione
L’analisi di regressione viene spesso utilizzata per modellare o analizzare i dati. La maggior parte degli analisti di sondaggi la utilizza per capire la relazione tra le variabili, che può essere ulteriormente utilizzata per prevedere un risultato preciso.
Ad esempio – Supponiamo che un’azienda produttrice di bevande analcoliche voglia espandere la propria unità produttiva in una nuova sede. Prima di procedere, l’azienda vuole analizzare il suo modello di generazione dei ricavi e i vari fattori che potrebbero influenzarlo. Per questo motivo, l’azienda conduce un’indagine online con un questionario specifico.
Dopo aver utilizzato l’analisi di regressione, diventa più facile per l’azienda analizzare i risultati del sondaggio e capire la relazione tra diverse variabili come l’elettricità e il fatturato – in questo caso, il fatturato è la variabile dipendente.
IMPARARE SU: Livello di analisi
Inoltre, la comprensione della relazione tra diverse variabili indipendenti come i prezzi, il numero di lavoratori e la logistica con il fatturato aiuta l’azienda a stimare l’impatto dei vari fattori sulle vendite e sui profitti.
I ricercatori di sondaggi utilizzano spesso questa tecnica per esaminare e trovare una correlazione tra diverse variabili di interesse. Offre l’opportunità di valutare l’influenza di diverse variabili indipendenti su una variabile dipendente.
Nel complesso, l’analisi di regressione risparmia ai ricercatori ulteriori sforzi per organizzare diverse variabili indipendenti in tabelle e testare o calcolare il loro effetto su una variabile dipendente. Diversi tipi di metodi di ricerca analitica sono ampiamente utilizzati per valutare nuove idee commerciali e prendere decisioni informate.
Tipi di analisi di regressione
I ricercatori di solito iniziano imparando prima la regressione lineare e quella logistica. A causa della conoscenza diffusa di questi due metodi e della facilità di applicazione, molti analisti pensano che esistano solo due tipi di modelli. Ogni modello ha la sua specialità e la sua capacità di funzionare se vengono soddisfatte determinate condizioni.
Questo blog spiega i sette tipi di metodi di analisi di regressione multipla comunemente utilizzati per interpretare i dati enumerati in vari formati.
01. Analisi di regressione lineare
Si tratta di una delle tecniche di modellazione più conosciute, in quanto è tra i primi metodi di analisi di regressione d’elite adottati dalle persone al momento dell’apprendimento della modellazione predittiva. In questo caso, la variabile dipendente è continua e la variabile indipendente è spesso continua o discreta con una linea di regressione lineare.
Tieni presente che la regressione lineare multipla prevede più di una variabile indipendente rispetto alla regressione lineare semplice. Pertanto, la regressione lineare è da utilizzare solo quando esiste una relazione lineare tra la variabile indipendente e quella dipendente.
Esempio
Un’azienda può utilizzare la regressione lineare per misurare l’efficacia delle campagne di marketing, dei prezzi e delle promozioni sulle vendite di un prodotto. Supponiamo che un’azienda che vende attrezzature sportive voglia capire se i fondi che ha investito nel marketing e nel branding dei suoi prodotti le hanno dato un ritorno sostanziale o meno.
La regressione lineare è il metodo statistico migliore per interpretare i risultati. L’aspetto migliore della regressione lineare è che aiuta anche ad analizzare l’impatto oscuro di ogni attività di marketing e branding, controllando però il potenziale dei componenti per regolare le vendite.
Se l’azienda sta conducendo due o più campagne pubblicitarie contemporaneamente, una in televisione e due alla radio, la regressione lineare può facilmente analizzare l’influenza indipendente e combinata di queste pubblicità.
IMPARARE SU: Progetti di analisi dei dati
02. Analisi di regressione logistica
La regressione logistica è comunemente utilizzata per determinare la probabilità di successo e di fallimento di un evento. La regressione logistica viene utilizzata quando la variabile dipendente è binaria, come 0/1, Vero/Falso o Sì/No. Quindi, si può dire che la regressione logistica viene utilizzata per analizzare le domande a risposta chiusa di un sondaggio o le domande che richiedono risposte numeriche in un sondaggio.
La regressione logistica non richiede una relazione lineare tra una variabile dipendente e una indipendente, proprio come la regressione lineare. La regressione logistica applica una trasformazione logica non lineare per prevedere l’odds ratio; pertanto, gestisce facilmente vari tipi di relazioni tra una variabile dipendente e una indipendente.
Esempio
La regressione logistica è ampiamente utilizzata per analizzare i dati categorici, in particolare per i dati a risposta binaria nella modellazione dei dati aziendali. Più spesso, la regressione logistica viene utilizzata quando la variabile dipendente è categorica, come ad esempio per prevedere se la dichiarazione di salute fatta da una persona è reale(1) o fraudolenta, per capire se il tumore è maligno(1) o meno.
Le aziende utilizzano la regressione logistica per prevedere se i consumatori di una determinata fascia demografica acquisteranno il loro prodotto o quello della concorrenza in base a età, reddito, sesso, razza, stato di residenza, acquisti precedenti, ecc.
03. Analisi di regressione polinomiale
La regressione polinomiale è comunemente utilizzata per analizzare i dati curvilinei quando la potenza di una variabile indipendente è superiore a 1. In questo metodo di analisi della regressione, la linea migliore non è mai una “linea retta” ma sempre una “linea curva” che si adatta ai punti dei dati.
Tieni presente che è meglio utilizzare la regressione polinomiale quando due o più variabili hanno degli esponenti e altre no.
Inoltre, è in grado di modellare dati separabili in modo non lineare, offrendo la possibilità di scegliere l’esatto esponente per ogni variabile e con il pieno controllo delle funzioni di modellazione disponibili.
Esempio
Se combinata con l’analisi della superficie di risposta, la regressione polinomiale è considerata uno dei metodi statistici sofisticati comunemente utilizzati nella ricerca sul feedback multisorgente. La regressione polinomiale viene utilizzata soprattutto nei settori finanziari e assicurativi in cui la relazione tra le variabili dipendenti e indipendenti è curvilinea.
Supponiamo che una persona voglia pianificare le spese determinando il tempo necessario per guadagnare una somma definitiva. La regressione polinomiale, prendendo in considerazione il suo reddito e prevedendo le spese, può facilmente determinare il tempo esatto in cui deve lavorare per guadagnare quella somma specifica.
04. Analisi di regressione graduale
Si tratta di un processo semi-automatico con il quale si costruisce un modello statistico aggiungendo o rimuovendo la variabile dipendente in base alle statistiche t dei coefficienti stimati.
Se utilizzata correttamente, la regressione stepwise ti fornirà dati più potenti di qualsiasi altro metodo. Funziona bene quando si lavora con un gran numero di variabili indipendenti. Non fa altro che perfezionare il modello dell ‘unità d’analisi, inserendo le variabili in modo casuale.
L’analisi di regressione stepwise è consigliata quando ci sono più variabili indipendenti e la selezione delle variabili indipendenti avviene automaticamente senza l’intervento umano.
Nella modellazione di regressione stepwise, la variabile viene aggiunta o sottratta dall’insieme delle variabili esplicative. L’insieme delle variabili aggiunte o rimosse viene scelto in base alle statistiche di test del coefficiente stimato.
Esempio
Supponiamo di avere una serie di variabili indipendenti come l’età, il peso, la superficie corporea, la durata dell’ipertensione, il polso basale e l’indice di stress, in base alle quali si vuole analizzare l’impatto sulla pressione sanguigna.
Nella regressione a gradini, il miglior sottoinsieme di variabili indipendenti viene scelto automaticamente; si inizia scegliendo nessuna variabile per procedere oltre (aggiungendo una variabile alla volta) oppure si inizia con tutte le variabili del modello e si procede a ritroso (eliminando una variabile alla volta).
Quindi, utilizzando l’analisi di regressione, è possibile calcolare l’impatto di ciascuna o di un gruppo di variabili sulla pressione sanguigna.
05. Analisi di regressione di cresta
La regressione di Ridge si basa su un metodo dei minimi quadrati ordinari che viene utilizzato per analizzare i dati di multicollinearità (dati in cui le variabili indipendenti sono altamente correlate). La collinearità può essere spiegata come una relazione quasi lineare tra le variabili.
In presenza di multicollinearità, le stime dei minimi quadrati saranno imparziali, ma se la differenza tra di esse è maggiore, allora potrebbe essere molto lontana dal valore reale. Tuttavia, la regressione ridge elimina gli errori standard aggiungendo un certo grado di distorsione alle stime della regressione con l’obiettivo di fornire stime più affidabili.
Se volete, potete anche imparare a conoscere i bias di selezione attraverso il nostro blog.
Nota bene: i presupposti derivati dalla regressione ridge sono simili a quelli della regressione ai minimi quadrati, con l’unica differenza della normalità. Sebbene il valore del coefficiente sia ristretto nella regressione ridge, non raggiunge mai lo zero suggerendo l’incapacità di selezionare le variabili.
Esempio
Supponiamo che tu sia pazzo di due chitarristi che si esibiscono dal vivo a un evento vicino a te e che tu vada a vedere la loro performance con l’intento di scoprire chi è il chitarrista migliore. Ma quando inizia l’esibizione, noti che entrambi suonano note nere e blu allo stesso tempo.
È possibile individuare il chitarrista che ha il maggiore impatto sul suono quando entrambi suonano forte e veloce? Poiché entrambi suonano note diverse, è sostanzialmente difficile differenziarli, il che rappresenta il caso migliore di multicollinearità, che tende ad aumentare gli errori standard dei coefficienti.
La regressione di Ridge affronta la multicollinearità in casi come questi e include una stima della polarizzazione o del restringimento per ottenere i risultati.
06. Analisi di regressione Lasso
Lasso (Least Absolute Shrinkage and Selection Operator) è simile alla regressione ridge; tuttavia, utilizza un bias in valore assoluto invece del bias quadratico utilizzato nella regressione ridge.
È stata sviluppata nel 1989 come alternativa alla tradizionale stima dei minimi quadrati con l’intento di risolvere la maggior parte dei problemi legati all’overfitting quando i dati hanno un gran numero di variabili indipendenti.
Lasso ha la capacità di eseguire entrambe le operazioni: selezionare le variabili e regolarizzarle con una soglia morbida. L’applicazione della regressione Lasso facilita la derivazione di un sottoinsieme di predittori dalla minimizzazione degli errori di previsione durante l’analisi di una risposta quantitativa.
Si noti che i coefficienti di regressione che raggiungono il valore zero dopo il restringimento sono esclusi dal modello Lazo. Al contrario, i coefficienti di regressione che hanno un valore superiore a zero sono fortemente associati alle variabili di risposta, laddove le variabili esplicative possono essere quantitative, categoriche o entrambe.
Esempio
Supponiamo che un’azienda automobilistica voglia effettuare una ricerca sul consumo medio di carburante delle auto negli Stati Uniti. Per i campioni ha scelto 32 modelli di auto e 10 caratteristiche del design dell’automobile: numero di cilindri, cilindrata, potenza lorda, rapporto dell’asse posteriore, peso, tempo di percorrenza di ¼ di miglio, rispetto a motore, trasmissione, numero di marce e numero di carburatori.
Come puoi vedere, la correlazione tra la variabile di risposta mpg (miglia per gallone) è estremamente correlata ad alcune variabili come peso, cilindrata, numero di cilindri e cavalli. Il problema può essere analizzato utilizzando il pacchetto glmnet di R e la regressione lasso per la selezione delle caratteristiche.
07. Analisi di regressione della rete elastica
Si tratta di una miscela di modelli di regressione ridge e lasso addestrati con norme L1 e L2. La rete elastica produce un effetto di raggruppamento per cui i predittori fortemente correlati tendono a entrare/uscire insieme dal modello. L’utilizzo del modello di regressione a rete elastica è consigliato quando il numero di predittori è di gran lunga superiore al numero di osservazioni.
Si noti che il modello di regressione a rete elastica è nato come opzione al modello di regressione lasso, poiché la sezione delle variabili di lasso dipendeva troppo dai dati, rendendola instabile. Utilizzando la regressione a rete elastica, gli statistici sono diventati capaci di superare le penalizzazioni della regressione ridge e della regressione lasso solo per ottenere il meglio da entrambi i modelli.
Esempio
Un team di ricerca clinica che ha accesso a un set di dati microarray sulla leucemia (LEU) era interessato a costruire una regola diagnostica basata sul livello di espressione dei campioni di geni presentati per prevedere il tipo di leucemia. Il set di dati a disposizione consisteva in un gran numero di geni e pochi campioni.
Inoltre, è stato dato loro un set specifico di campioni da utilizzare come campioni di addestramento, di cui alcuni infetti da leucemia di tipo 1 (leucemia linfoblastica acuta) e altri da leucemia di tipo 2 (leucemia mieloide acuta).
L’adattamento del modello e la selezione dei parametri di regolazione mediante CV decuplicato sono stati eseguiti sui dati di formazione. Poi hanno confrontato le prestazioni di questi metodi calcolando il loro errore quadratico medio di previsione sui dati di prova per ottenere i risultati necessari.
Utilizzo dell’analisi di regressione nelle ricerche di mercato
Un’indagine di mercato si concentra su tre matrici principali: la Soddisfazione del Cliente, la Fedeltà del Cliente e l’Advocacy del Cliente. Ricorda che, sebbene queste matrici ci parlino della salute e delle intenzioni dei clienti, non ci dicono come migliorare la posizione. Per questo motivo, un questionario approfondito volto a chiedere ai consumatori le ragioni della loro insoddisfazione è sicuramente un modo per ottenere informazioni pratiche.
Tuttavia, è stato riscontrato che le persone spesso faticano a esprimere la propria motivazione o demotivazione o a descrivere la propria soddisfazione o insoddisfazione. Inoltre, le persone danno sempre un’importanza eccessiva ad alcuni fattori razionali, come il prezzo, il packaging, ecc. In generale, agisce come strumento analitico e previsionale nelle ricerche di mercato.
Se utilizzata come strumento di previsione, l’analisi di regressione può determinare i dati di vendita di un’organizzazione tenendo conto dei dati di mercato esterni. Una multinazionale conduce un’indagine di mercato per capire l’impatto di vari fattori come il PIL (Prodotto Interno Lordo), l’IPC (Indice dei Prezzi al Consumo) e altri fattori simili sul suo modello di generazione dei ricavi.
Ovviamente, l’analisi di regressione in considerazione degli indicatori di marketing previsti è stata utilizzata per prevedere un’ipotesi di ricavi che saranno generati nei trimestri futuri e persino negli anni futuri. Tuttavia, più si va avanti nel futuro, i dati diventeranno più inaffidabili, lasciando un ampio margine di errore.
Caso di studio sull’utilizzo dell’analisi di regressione
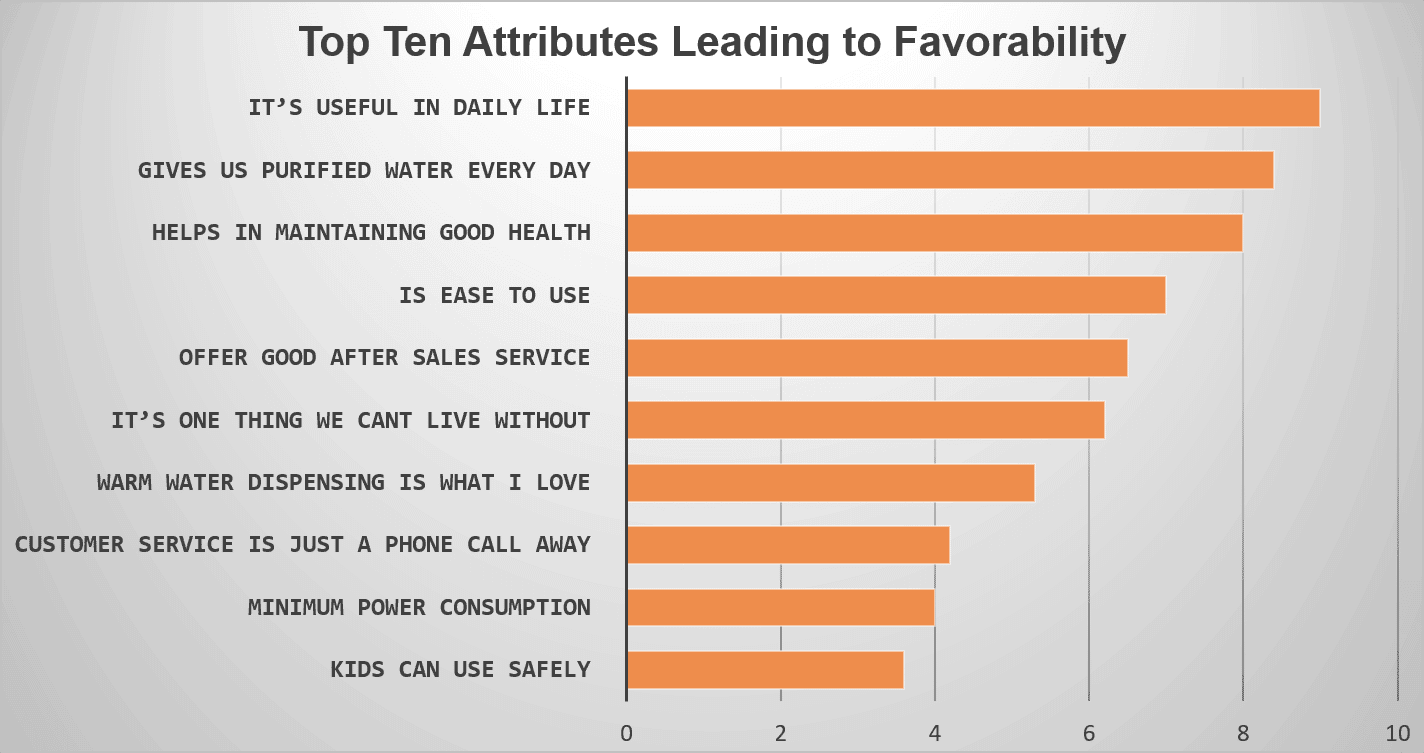
Un’azienda produttrice di depuratori d’acqua voleva capire quali fossero i fattori che determinano il gradimento del marchio. Il sondaggio era il mezzo migliore per raggiungere i clienti attuali e potenziali. È stata pianificata un’indagine su larga scala tra i consumatori ed è stato preparato un questionario discreto utilizzando il miglior strumento di indagine.
Nel sondaggio sono state poste una serie di domande relative al marchio, alla preferibilità, alla soddisfazione e alla probabile insoddisfazione. Dopo aver ottenuto le risposte ottimali al sondaggio, è stata utilizzata l’analisi di regressione per restringere la top ten dei fattori che determinano il gradimento del marchio.
Tutti i dieci attributi ricavati (citati nell’immagine sottostante) in un modo o nell’altro hanno evidenziato la loro importanza nell’influenzare il gradimento di quello specifico marchio di depuratori d’acqua.
In che modo l’analisi di regressione ricava informazioni dai sondaggi?
È facile eseguire un’analisi di regressione utilizzando Excel o SPSS, ma nel farlo è necessario comprendere l’importanza dei quattro numeri nell’interpretazione dei dati.
I primi due numeri dei quattro riguardano direttamente il modello di regressione.
- Valore F: Aiuta a misurare la significatività statistica del modello di indagine. Ricorda che un valore F significativamente inferiore a 0,05 è considerato più significativo. Un valore F inferiore a 0,05 garantisce che i risultati dell’analisi del sondaggio non siano frutto del caso.
- R-quadro: È il valore con cui le variabili indipendenti cercano di spiegare la quantità di movimento delle variabili dipendenti. Se il valore R-Squared è di 0,7, una variabile indipendente testata può spiegare il 70% del movimento della variabile dipendente. Ciò significa che il risultato dell’analisi del sondaggio che otterremo è di natura altamente predittiva e può essere considerato accurato.
Gli altri due numeri si riferiscono a ciascuna delle variabili indipendenti durante l’interpretazione dell’analisi di regressione.
- Valore P: Come il valore F, anche il valore P è statisticamente significativo. Inoltre, in questo caso indica quanto sia rilevante e statisticamente significativo l’effetto della variabile indipendente. Anche in questo caso, cerchiamo un valore inferiore a 0,05.
- Interpretazione: Il quarto numero si riferisce al coefficiente ottenuto dopo aver misurato l’impatto delle variabili. Ad esempio, testiamo più variabili indipendenti per ottenere un coefficiente. Il coefficiente ci dice “di quale valore ci si aspetta che la variabile dipendente aumenti quando le variabili indipendenti (che stiamo considerando) aumentano di uno mentre tutte le altre variabili indipendenti rimangono ferme allo stesso valore”.
In alcuni casi, il coefficiente semplice viene sostituito da un coefficiente standardizzato che dimostra il contributo di ogni variabile indipendente per spostare o determinare un cambiamento nella variabile dipendente.
Vantaggi dell’utilizzo dell’analisi di regressione in un sondaggio online
01. Ottenere l’accesso all’analisi predittiva
Sai che utilizzare l’analisi di regressione per comprendere i risultati di un’indagine commerciale significa avere il potere di svelare opportunità e rischi futuri?
Ad esempio, dopo aver visto una particolare fascia pubblicitaria in televisione, possiamo prevedere il numero esatto di aziende utilizzando quei dati per stimare un’offerta massima per quella fascia. L’intero settore finanziario e assicurativo dipende molto dall’analisi di regressione dei dati delle indagini per identificare tendenze e opportunità per una pianificazione e un processo decisionale più accurati.
02. Migliorare l’efficienza operativa
Sai che le aziende utilizzano l’analisi di regressione per ottimizzare i processi aziendali?
Ad esempio, prima di lanciare una nuova linea di prodotti, le aziende conducono indagini sui consumatori per comprendere meglio l’impatto di vari fattori sulla produzione, il confezionamento, la distribuzione e il consumo del prodotto.
Una previsione basata sui dati aiuta a eliminare le congetture, le ipotesi e la politica interna dal processo decisionale. Una comprensione più approfondita delle aree che influenzano l’efficienza operativa e i ricavi porta a una migliore ottimizzazione del business.
03. Supporto quantitativo al processo decisionale
Le indagini aziendali oggi generano una grande quantità di dati relativi a finanze, ricavi, operazioni, acquisti, ecc. e i proprietari delle aziende dipendono fortemente da vari modelli di analisi dei dati per prendere decisioni aziendali informate.
Ad esempio, l’analisi di regressione aiuta le aziende a prendere decisioni strategiche informate sulla forza lavoro. La conduzione e l’interpretazione dei risultati dei sondaggi sui dipendenti, come i sondaggi sul coinvolgimento dei dipendenti, i sondaggi sulla soddisfazione dei dipendenti, i sondaggi sul miglioramento dei dipendenti, i sondaggi sull’uscita dei dipendenti e così via, aumentano la comprensione del rapporto tra i dipendenti e l’azienda.
Inoltre, aiuta a farsi un’idea precisa di alcuni problemi che influenzano la cultura lavorativa, l’ambiente di lavoro e la produttività dell’organizzazione. Inoltre, le interpretazioni intelligenti orientate al business riducono l’enorme mole di dati grezzi in informazioni attuabili per prendere decisioni più consapevoli.
04. Prevenire gli errori dovuti alle intuizioni
Sapendo come utilizzare l’analisi di regressione per interpretare i risultati di un sondaggio, si può facilmente fornire un supporto fattuale al management per prendere decisioni informate; ma sai che aiuta anche a evitare errori di valutazione?
Ad esempio, il direttore di un centro commerciale pensa che se prolunga l’orario di chiusura del centro commerciale, le vendite aumenteranno. L’analisi di regressione contraddice la convinzione che la previsione di un aumento delle entrate dovuto all’incremento delle vendite non supporterà l’aumento delle spese operative derivanti dall’allungamento dell’orario di lavoro.
Conclusione
L’analisi di regressione è un metodo statistico utile per modellare e comprendere le relazioni tra le variabili. Offre numerosi vantaggi a vari tipi di dati e interazioni. Ricercatori e analisti possono ottenere utili informazioni sui fattori che influenzano una variabile dipendente e utilizzare i risultati per prendere decisioni informate.
Con QuestionPro Research puoi migliorare l’efficienza e l’accuratezza dell’analisi di regressione semplificando i processi di raccolta dati, analisi e reporting. L’interfaccia user-friendly della piattaforma e l’ampia gamma di funzioni la rendono uno strumento prezioso per i ricercatori e gli analisti che conducono analisi di regressione nell’ambito dei loro progetti di ricerca.
Iscriviti alla prova gratuita oggi stesso e fai volare i tuoi sogni di ricerca!



