La campana gaussiana, nota anche come distribuzione normale, prende il nome dal matematico tedesco Carl Friedrich Gauss ed è diventata un pilastro essenziale dell’analisi statistica e viene utilizzata in diverse discipline.
In questo articolo esploriamo la campana gaussiana dalla sua definizione alle sue applicazioni pratiche, evidenziandone i vantaggi e le caratteristiche distintive.
Che cos’è una campana gaussiana?
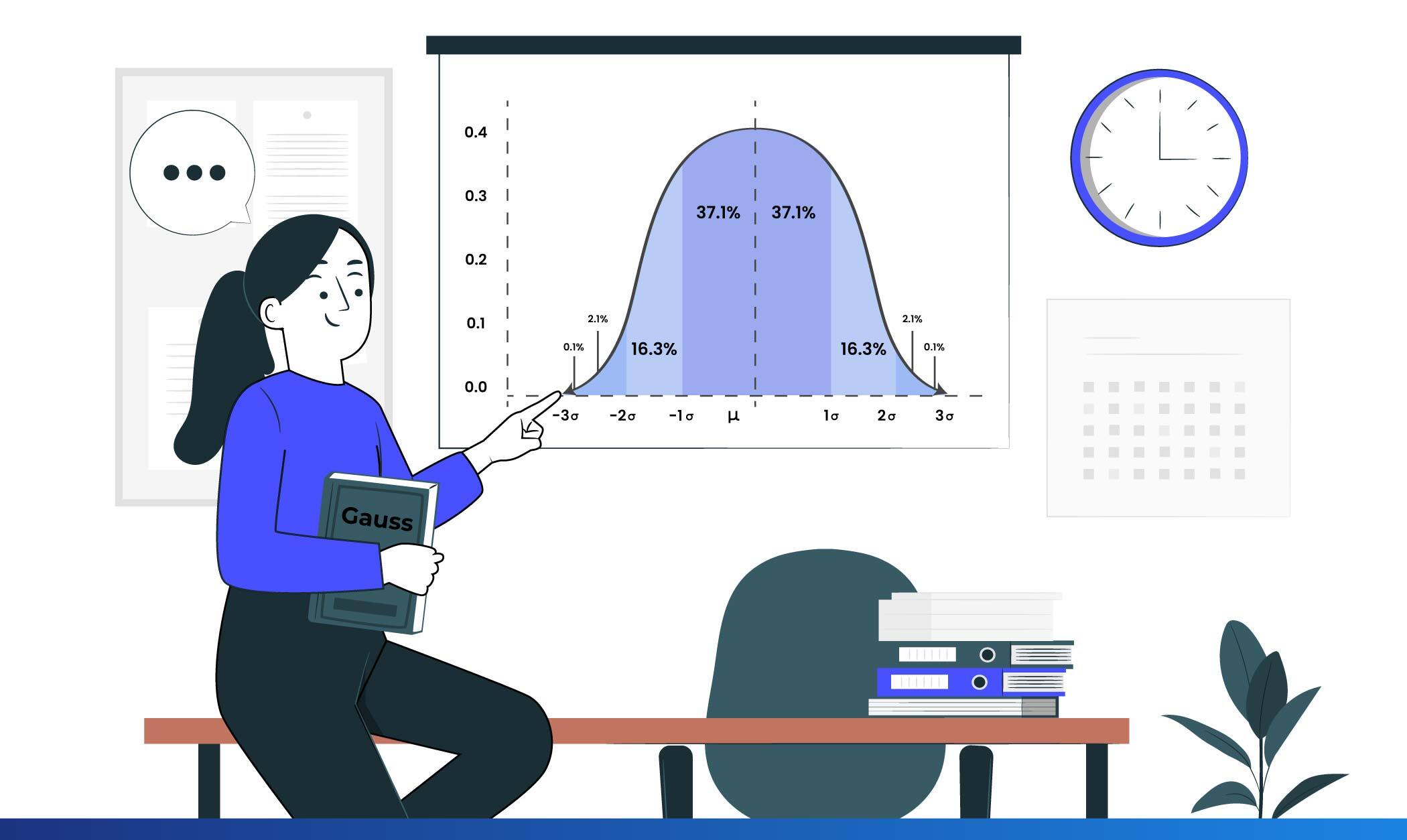
La campana gaussiana, o distribuzione normale, è una funzione matematica che descrive il modo in cui i dati sono distribuiti in un insieme. È caratterizzata da una forma simmetrica e dal famoso aspetto a campana, con la maggior parte dei dati concentrati intorno alla media e che si disperdono uniformemente ai lati. La funzione è definita da due parametri principali: la media, che rappresenta il centro della distribuzione, e la deviazione standard, che misura la dispersione dei dati.
La sua forma simmetrica significa che metà dei dati si trovano a sinistra della media e metà a destra. Inoltre, circa il 68% dei dati rientra in una deviazione standard della media, mentre il 95% rientra in due deviazioni standard.
Un’altra caratteristica interessante è che, indipendentemente dalla forma della distribuzione originale, quando si accumulano abbastanza dati, la distribuzione tende a seguire una forma a campana gaussiana. Questo fenomeno è noto come Teorema del Limite Centrale, che sottolinea la pervasività di questa distribuzione nell’analisi statistica.
Vantaggi della campana gaussiana: perché è così potente?
La popolarità della campana gaussiana risiede in diversi vantaggi chiave. Innanzitutto, è molto intuitiva e facile da capire, il che la rende uno strumento accessibile anche a chi non ha un’ampia preparazione matematica. Inoltre, la sua ampia applicabilità le permette di modellare con precisione un’ampia gamma di situazioni del mondo reale.
Un altro vantaggio fondamentale è la capacità di riassumere le informazioni in due parametri: la media e la deviazione standard. Questo semplifica notevolmente l’analisi e l’interpretazione dei dati, permettendo a ricercatori e analisti di ottenere informazioni preziose in modo efficiente.
Il Teorema del Limite Centrale afferma che, data una dimensione del campione sufficientemente grande, la distribuzione delle medie campionarie approssima una distribuzione normale, indipendentemente dalla forma della distribuzione originale. Questo rende la campana gaussiana un potente strumento per l’analisi di grandi insiemi di dati.
La campana gaussiana è fondamentale per molti test statistici, come il test t di Student e il test chi-quadro. Questi test si basano su ipotesi di normalità per fare inferenze sulle popolazioni.
Usi della campana gaussiana
La campana gaussiana viene applicata in un’ampia varietà di campi, dalla fisica e dalla biologia all’economia e alla psicologia. In statistica, viene comunemente utilizzata per modellare fenomeni naturali, come l’altezza di una popolazione o i punteggi dei test. Inoltre, questa distribuzione viene utilizzata come base per altri strumenti statistici e modelli più complessi.
La campana gaussiana, o distribuzione normale, è utilizzata in un’ampia varietà di campi grazie alla sua versatilità e alla capacità di modellare numerosi fenomeni. Alcuni degli usi più comuni includono:
Statistiche descrittive:
La campana gaussiana è fondamentale per descrivere la distribuzione dei dati in una popolazione. Viene utilizzata per riassumere e comprendere la tendenza centrale e la dispersione di una serie di dati.
Inferenza statistica:
Nell’inferenza statistica, la campana gaussiana è fondamentale per fare previsioni e stime. Permette di calcolare gli intervalli di confidenza e di eseguire test di ipotesi, fornendo strumenti fondamentali per il processo decisionale basato sui dati.
Ricerca psicologica:
In psicologia, la campana gaussiana viene utilizzata per modellare diversi fenomeni, come la distribuzione dei quozienti di intelligenza (QI) in una popolazione. Viene utilizzata anche negli studi comportamentali e nell’analisi dei risultati dei test psicometrici.
Economia e finanza:
In economia e finanza, la campana gaussiana viene utilizzata per modellare la variabilità dei rendimenti delle attività finanziarie. Il modello dei rendimenti logaritmici segue in molti casi una distribuzione normale, il che facilita la valutazione del rischio e il processo decisionale sugli investimenti.
Biologia e medicina:
In biologia, la distribuzione normale si ritrova in fenomeni come l’altezza di una popolazione o la distribuzione del peso in una specie. In medicina, viene applicata per analizzare i dati biometrici e valutare l’efficacia dei trattamenti, tra gli altri usi.
Controllo qualità:
La campana gaussiana viene utilizzata nel controllo qualità per valutare la coerenza e la variabilità nella produzione di beni e servizi. Permette di stabilire i limiti di tolleranza e di individuare eventuali deviazioni nei processi produttivi.
Modellazione dei fenomeni naturali:
In diverse discipline scientifiche, come la fisica, la meteorologia e la geologia, la campana gaussiana viene utilizzata per modellare la distribuzione di variabili come la velocità del vento, la temperatura o la concentrazione di sostanze chimiche in una determinata area.
Apprendimento automatico e scienza dei dati:
Nel campo dell’apprendimento automatico, la campana gaussiana viene utilizzata come ipotesi iniziale in molti algoritmi e modelli. Inoltre, è comune assumere che gli errori di previsione seguano una distribuzione normale, il che facilita lo sviluppo e l’interpretazione dei modelli.
Esempio di campana gaussiana: Valutazione del rendimento scolastico
Immaginiamo di analizzare il rendimento scolastico degli studenti di una scuola secondaria. Vogliamo capire come si distribuiscono i voti in un esame di matematica e utilizziamo la campana gaussiana per ottenere informazioni preziose sul rendimento complessivo della classe.
Fase 1: Raccolta dei dati
Otteniamo i punteggi di tutti gli studenti nel test di matematica. Supponiamo di aver raccolto i seguenti punteggi su una scala da 0 a 100:
78, 82, 85, 88, 90, 92, 94, 96, 98, 100
Fase 2: Calcolo della media e della deviazione standard
Calcoliamo la media e la deviazione standard di questi punteggi. Supponiamo che la media sia 90 e che la deviazione standard sia 6. Questi valori servono semplicemente a illustrare l’esempio; in uno scenario reale, verrebbero calcolati in base ai dati reali.
Passo 3: Creare la campana gaussiana
Con la media e la deviazione standard, possiamo creare la campana gaussiana che descrive la distribuzione dei voti. La maggior parte degli studenti si concentra intorno alla media e la forma a campana riflette la probabilità di ottenere voti diversi.
Fase 4: Interpretazione della campana gaussiana
- 68% degli studenti: Circa il 68% degli studenti otterrà voti che rientrano in una deviazione standard della media, ovvero tra 84 e 96.
- 95% degli studenti: Circa il 95% degli studenti avrà voti che rientrano in due deviazioni standard della media, nell’intervallo tra 78 e 102.
- 99,7% degli studenti: Praticamente tutti gli studenti (99,7%) otterranno un punteggio entro tre deviazioni standard dalla media, tra 72 e 108.
Fase 5: processo decisionale e valutazione delle prestazioni
Grazie a questa distribuzione, gli educatori possono prendere decisioni informate sull’efficacia dei test e dell’insegnamento. Ad esempio, se un gran numero di studenti ottiene un punteggio inferiore alla media, questo potrebbe indicare aree di miglioramento nell’insegnamento. Inoltre, la campana gaussiana fornisce una chiara comprensione della distribuzione dei voti, che può essere utile per definire gli standard di rendimento e le politiche educative.
In questo caso d’uso, la campana gaussiana non solo fornisce un riassunto visivo della distribuzione dei voti, ma offre anche strumenti preziosi per prendere decisioni didattiche basate su dati statistici. Questo esempio illustra come la distribuzione normale possa essere un potente strumento di valutazione e miglioramento continuo del rendimento scolastico.
Conclusione
In conclusione, la campana gaussiana è più di una semplice curva matematica: è uno strumento essenziale che ha dimostrato la sua utilità in diverse discipline. La sua semplicità, versatilità e capacità di riassumere dati complessi in parametri chiave la rendono un componente fondamentale dell’analisi statistica. Mentre continuiamo a esplorare e comprendere il mondo che ci circonda, la campana gaussiana continuerà a svolgere un ruolo cruciale nella nostra capacità di modellare e comprendere i fenomeni con precisione e chiarezza.
Se sei alla ricerca di strumenti per raccogliere dati di qualità per i tuoi prossimi progetti, ricorda che QuestionPro può aiutarti. Inizia creando un account gratuito per il nostro software di sondaggi e scopri tutte le sue potenzialità.



