
La correlazione è un concetto fondamentale nella statistica e nell’analisi dei dati, che aiuta a comprendere la relazione tra due variabili. Sebbene vengano spesso evidenziate forti correlazioni positive o negative, la correlazione zero è altrettanto importante.
Significa che non esiste una relazione lineare tra le variabili. In altre parole, le variazioni di una variabile non predicono le variazioni dell’altra.
In questo blog esploreremo il concetto di correlazione zero, fornendo una definizione chiara, esempi illustrativi e metodi per determinarla.
Che cos’è la correlazione zero?
La correlazione zero è un termine statistico che descrive una situazione in cui non esiste una relazione lineare tra due variabili. Quando due variabili hanno correlazione zero, le variazioni di una variabile non predicono le variazioni dell’altra. Il coefficiente di correlazione, che misura il grado e la direzione della relazione tra le variabili, è esattamente pari a zero in questo caso.
La comprensione di questa correlazione è importante nell’analisi statistica perché aiuta a identificare le variabili che non hanno una relazione predittiva tra loro, il che è fondamentale quando si costruiscono modelli statistici o si interpretano modelli di dati.
Perché è importante la correlazione zero?
La correlazione zero è un concetto importante nella statistica e nell’analisi dei dati per diversi motivi, come ad esempio:
Identifica l’indipendenza
Aiuta a identificare le variabili che sono linearmente indipendenti l’una dall’altra. Se due variabili hanno una correlazione nulla, le variazioni di una variabile non forniscono alcuna informazione sulle variazioni dell’altra. Questo è fondamentale per comprendere la struttura dei dati e le relazioni (o la loro mancanza) tra le variabili.
Migliora i modelli statistici
Nell’analisi di regressione e in altri modelli statistici, l’inclusione di variabili con questa correlazione con la variabile dipendente può aggiungere rumore e ridurre il potere predittivo del modello. Identificando ed escludendo tali variabili, i modelli possono essere semplificati e resi più efficienti, migliorando le prestazioni e l’interpretabilità.
Questa correlazione aiuta a evitare interpretazioni errate
La comprensione di questa correlazione impedisce un’interpretazione errata dei dati.
- Ad esempio, un ricercatore potrebbe dedurre erroneamente una relazione tra due variabili basandosi sull’intuizione o sulle osservazioni iniziali.
Calcolare il coefficiente di correlazione e scoprire che è pari a zero chiarisce che non esiste una relazione lineare, evitando false conclusioni.
Evidenzia le relazioni non lineari
Evidenzia la possibilità di relazioni non lineari. Se due variabili hanno una correlazione nulla, non significa necessariamente che non siano correlate: potrebbero avere una relazione complessa e non lineare. Riconoscere questo aspetto può suggerire ulteriori indagini utilizzando altri metodi, come la regressione non lineare o le trasformazioni dei dati.
La correlazione aiuta a guidare il disegno sperimentale
Nella progettazione sperimentale, sapere quali variabili hanno correlazione zero può guidare la selezione delle variabili da includere o controllare. Questo aiuta a progettare esperimenti più robusti in cui l’influenza delle variabili irrilevanti viene ridotta al minimo, portando a risultati più chiari e affidabili.
Comprende il comportamento delle variabili
Fornisce approfondimenti sul comportamento delle variabili in un insieme di dati. Nell’analisi finanziaria, capire quali attività hanno una correlazione nulla tra loro può essere utile per la diversificazione del portafoglio, in quanto la combinazione di tali attività può ridurre il rischio complessivo.
Supporta la verifica delle ipotesi
Nei test di ipotesi, questa correlazione è spesso un’ipotesi nulla.
- Ad esempio, nel verificare se due variabili sono correlate, l’ipotesi nulla potrebbe affermare che la correlazione tra di esse è pari a zero.
Stabilire se questo è vero o falso aiuta a convalidare o confutare le ipotesi.
Quali sono gli esempi di correlazione zero?
Esempi di questa correlazione, in cui i cambiamenti di una variabile non corrispondono ai cambiamenti di un’altra variabile, si possono trovare in vari campi, come ad esempio:
Campo di ricerca
Esempio: Numero di pubblicazioni scientifiche e gusto di gelato preferito
Uno studio analizza la relazione tra il numero di pubblicazioni scientifiche di un ricercatore e il suo gusto di gelato preferito.
Non esiste una connessione logica tra il numero di articoli scientifici pubblicati da un ricercatore e la sua preferenza per un particolare gusto di gelato. Di conseguenza, ci si aspetta che queste due variabili presentino questa correlazione.
Campo dell’istruzione
Esempio: Il numero di scarpe degli studenti e i loro voti in matematica
Uno studio educativo esamina se esiste una relazione tra i numeri di scarpe degli studenti e i loro voti in matematica.
Il numero di scarpe è una caratteristica fisica che non ha alcuna influenza sul rendimento scolastico di uno studente in matematica. Pertanto, è probabile che la correlazione tra il numero di scarpe e i voti in matematica sia pari a zero.
Campo dell’assistenza sanitaria
Esempio: Gruppo sanguigno e incidenza del raffreddore comune
Uno studio sanitario esamina se esiste una relazione tra il gruppo sanguigno di una persona e il numero di volte in cui prende il raffreddore comune in un anno.
Il gruppo sanguigno non è associato alla frequenza di contrarre il comune raffreddore, che è influenzato da vari altri fattori come l’esposizione ai virus e la forza del sistema immunitario. Di conseguenza, la correlazione tra il gruppo sanguigno e l’incidenza del raffreddore comune dovrebbe essere pari a zero.
Come identificare la correlazione zero?
Qui esploreremo come identificare questa correlazione attraverso l’ispezione visiva, il calcolo statistico, il test di ipotesi e l’analisi contestuale.
1. Ispezione visiva con i diagrammi di dispersione
I diagrammi di dispersione sono uno strumento efficace per valutare visivamente la relazione tra due variabili.
Crea un grafico a dispersione:
- Posiziona una variabile sull’asse x e l’altra sull’asse y.
- Cerca di individuare qualsiasi tendenza o modello distinguibile nei punti dati.
Identificare la correlazione:
- Se i punti sono sparsi in modo casuale senza una chiara tendenza (né verso l’alto né verso il basso), ciò suggerisce una correlazione.
- Una dispersione casuale implica che nessuna linea (sia essa retta o curva) può adattarsi bene ai punti dei dati.
Esempio:
- Taglie delle scarpe degli studenti rispetto ai voti di matematica: Se il grafico dei numeri di scarpe rispetto ai voti di matematica mostra una dispersione casuale di punti senza alcuna tendenza, questo indica una correlazione nulla.
2. Calcola il coefficiente di correlazione
Il coefficiente di correlazione di Pearson (r) è la misura più comune della correlazione lineare.
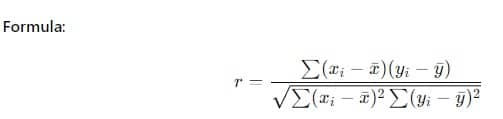
Passi:
- Raccogli i dati accoppiati per le due variabili.
- Trova la media di ogni variabile.
- Calcola la distanza di ciascun punto di dati dalla media.
- Moltiplica le deviazioni per ogni coppia e somma i prodotti.
- Usa la formula per trovare il coefficiente di correlazione.
Interpretare la correlazione:
Valore vicino a 0: se 𝑟 r è vicino a 0, indica una relazione lineare minima o nulla tra le variabili.
Esempio:
- Taglie delle scarpe e voti in matematica: Se l’𝑟 calcolato è approssimativamente pari a 0, si conferma una correlazione nulla.
3. Eseguire i test di ipotesi
I test di ipotesi statistica possono determinare se un coefficiente di correlazione osservato è significativamente diverso da zero.
Passi:
- Ipotesi nulla: Supponiamo che il coefficiente di correlazione sia pari a zero.
- Ipotesi alternativa: Supponiamo che il coefficiente di correlazione non sia pari a zero.
- Calcolo della statistica del test: usa un test t per il coefficiente di correlazione.
- Determina il valore p: Confronta il valore p con un livello di significatività (ad esempio, 0,05).
Correlazione zero:
- Se il valore p è superiore al livello di significatività, non rifiutare l’ipotesi nulla, suggerendo che la correlazione non è significativamente diversa da zero.
Esempio:
- Gruppo sanguigno e incidenza del raffreddore comune: Verificando la correlazione tra il gruppo sanguigno e l’incidenza del raffreddore comune, se il valore p è alto, indica che qualsiasi correlazione osservata non è statisticamente significativa, sostenendo una correlazione nulla.
4. Comprendere l’analisi contestuale
Comprendere il contesto e il background teorico delle variabili è essenziale per interpretare i risultati delle correlazioni.
Passi:
- Esamina le variabili: Considera la natura e le relazioni previste tra le variabili.
- Applicare la conoscenza del dominio: Usa le conoscenze del settore per ipotizzare se una relazione è prevista.
Correlazione zero:
- Se la teoria e le ricerche precedenti non suggeriscono alcuna relazione logica, ciò supporta la scoperta di questa correlazione.
Esempio:
- Gruppo sanguigno e incidenza del raffreddore comune: Sapere che il gruppo sanguigno non influisce sulla suscettibilità al raffreddore comune supporta l’interpretazione di una correlazione nulla, se trovata.
Correlazione negativa vs. positiva vs. correlazione zero
La correlazione è una misura statistica che descrive la forza e la direzione della relazione tra due variabili. Ecco una spiegazione dettagliata della correlazione negativa, positiva e nulla:
Correlazione positiva
- Definizione: Una correlazione positiva si verifica quando due variabili si muovono nella stessa direzione. Quando una variabile aumenta, anche l’altra aumenta e quando una diminuisce, anche l’altra diminuisce.
- Esempio: La relazione tra altezza e peso. In genere, all’aumentare dell’altezza di una persona, tende ad aumentare anche il suo peso.
- Rappresentazione grafica: In un grafico a dispersione, i punti tendono a raggrupparsi attorno a una linea che degrada verso l’alto da sinistra a destra.
Correlazione negativa
- Definizione: Una correlazione negativa si verifica quando due variabili si muovono in direzioni opposte. Quando una variabile aumenta, l’altra diminuisce e viceversa.
- Esempio: La relazione tra il tempo dedicato allo studio e il numero di errori commessi in un test. In genere, all’aumentare del tempo dedicato allo studio, diminuisce il numero di errori.
- Rappresentazione grafica: In un grafico a dispersione, i punti tendono a raggrupparsi attorno a una linea che degrada verso il basso da sinistra a destra.
Correlazione zero
- Definizione: Indica che non esiste una relazione tra le due variabili. Le variazioni di una variabile non predicono le variazioni dell’altra variabile.
- Esempio: La relazione tra il numero di scarpe di una persona e il suo quoziente di intelligenza (QI). Non esiste una connessione logica tra queste due variabili.
- Rappresentazione grafica: In un grafico a dispersione, i punti sono distribuiti in modo casuale senza un modello o una pendenza distinguibili.
In che modo QuestionPro può aiutare nell’analisi delle correlazioni?
QuestionPro, una solida piattaforma di sondaggi, offre strumenti completi per facilitare l’analisi di correlazione in modo efficace. Ecco come QuestionPro può aiutarti a condurre l’analisi di correlazione:
Raccolta dati senza sforzo
QuestionPro semplifica il processo di raccolta dei dati grazie ai suoi strumenti di creazione di sondaggi facili da usare. Puoi progettare e distribuire sondaggi per raccogliere dati quantitativi su diverse variabili di interesse. La piattaforma supporta diversi tipi di domande, consentendoti di acquisire dati dettagliati e rilevanti in modo efficiente.
Analisi automatizzata dei dati
Una volta raccolti i dati, QuestionPro fornisce strumenti di analisi integrati per l’analisi delle correlazioni. Puoi calcolare facilmente le correlazioni, che misurano la forza e la direzione della relazione lineare tra due variabili. Il coefficiente di correlazione lineare va da -1 a 1, dove:
- 1 indica una correlazione positiva perfetta.
- -1 indica una correlazione negativa perfetta.
- 0 indica l’assenza di correlazione.
Rappresentazione visiva
QuestionPro offre strumenti di visualizzazione per aiutarti a interpretare i risultati dell’analisi di correlazione. È possibile generare diagrammi di dispersione e matrici di correlazione per fornire una chiara rappresentazione grafica delle relazioni tra le variabili. Questo aiuto visivo è fondamentale per identificare rapidamente tendenze e modelli.
Identificare modelli e tendenze
Utilizzando l’analisi di correlazione di QuestionPro, i ricercatori hanno osservato la correlazione (positiva, negativa o nulla) tra le variabili:
- Correlazione positiva: Entrambe le variabili si muovono nella stessa direzione. Ad esempio, un aumento della spesa pubblicitaria può essere correlato a un aumento delle vendite.
- Correlazione negativa: Le variabili tendono a muoversi in direzioni opposte. Ad esempio, un aumento del tempo trascorso sullo schermo potrebbe essere correlato a una diminuzione del rendimento scolastico.
- Correlazione zero: Non esiste alcuna relazione tra le variabili. Ad esempio, il numero di anni di scuola potrebbe non essere correlato al numero di lettere del nome di una persona.
Applicazioni pratiche
L’analisi delle correlazioni in QuestionPro può essere utilizzata per diverse applicazioni pratiche, come ad esempio:
- Ricerche di mercato: Misura l’efficacia delle campagne di marketing correlando la spesa pubblicitaria ai risultati di vendita.
- Assistenza sanitaria: Valutare la relazione tra l’uso dei farmaci e i risultati dei pazienti, come i livelli di pressione sanguigna.
- Istruzione: Determina l’impatto delle abitudini di studio sul rendimento scolastico mettendo in relazione le ore di studio con i voti.
Conclusione
La correlazione zero tra due variabili indica l’assenza di una relazione lineare, indicando che le variazioni di una variabile non corrispondono alle variazioni di un’altra. Calcolando i coefficienti di correlazione e visualizzando i dati attraverso i grafici a dispersione, i ricercatori possono determinare con precisione se le variabili sono correlate, correlate positivamente, correlate negativamente o se mostrano questa correlazione.
L’uso di QuestionPro per l’analisi delle correlazioni nei tuoi sondaggi offre un modo potente per scoprire relazioni significative tra le variabili. Esplorando l’interfaccia intuitiva di QuestionPro, gli strumenti analitici avanzati e le funzioni di reporting complete, puoi condurre in modo efficiente l’analisi di correlazione e ricavare preziose informazioni dai tuoi dati. Contatta QuestionPro oggi stesso per maggiori informazioni!



