
The margin of error is an essential concept for understanding the accuracy and reliability of survey data. In this article, we’ll take a closer look at its definition and its calculation while providing examples of how it’s used in research.
We’ll also discuss the importance of considering the margin of error when interpreting survey results and how it can affect the conclusions drawn from the data.
So, whether you’re experienced or just starting your journey, this article is a must-read for anyone looking to master the art of margin of error and ensure the accuracy and reliability of their research. Let’s get started!
What is a Margin of Error?
The margin of error is a way to express how much the results of a survey or poll could differ from the actual truth. It’s a tool used in statistics to show the level of uncertainty in the data.
The margin of error is calculated based on factors like the sample size (how many people were surveyed) and the variability of the population. A larger sample size usually leads to a smaller margin of error, meaning the estimate is more accurate.
When you see a margin of error in surveys or polls, think of it as a cushion. It shows how much the numbers might shift if the survey were done again or with a different group of people. A smaller margin of error means more reliable results. In contrast, a larger margin of error suggests greater uncertainty in the findings.
In short, the margin of error helps us understand that while survey results can give us a good idea of public opinion, they’re not always 100% exact.
The margin of Error Calculation
In statistics, the margin of error is a crucial measure that defines the range within which the true value of a true population parameter is expected to lie based on sample data. It provides researchers with a sense of the precision and reliability of their survey results.
This sampling error can be significantly high if the entire population is not defined or in cases where the sample selection process is not carried out properly.
Every time a researcher conducts a statistical survey, a margin of error calculation is required. The universal formula for a sample is the following:

Analyzing the Formula
- p̂ : The sample proportion, representing the fraction of respondents or observations in the sample with a specific characteristic.
- n: The sample size indicates the total number of individuals or observations in the survey. A larger sample size reduces the margin of error.
- z: The Z-score, which corresponds to the confidence level you want to achieve.
Are you feeling a bit confused? Don’t worry! You can use our margin of error calculator.
Example for Margin of Error Calculation
For example, wine-tasting sessions conducted in vineyards depend on the quality and taste of the wines presented during the session. These wines represent the entire production, and depending on how well the visitors receive them, the feedback from them is generalized to the entire production.
The wine tasting will be effective only when visitors do not have a pattern, i.e., they’re chosen randomly. Wine goes through a process to be palatable, and similarly, visitors must go through a process to provide effective results.
The measurement components prove whether the wine bottles are worthy to represent the entire winery’s production or not. If a statistician states that the conducted survey will have a margin of error of plus or minus 5% at a 93% confidence interval formula. This means that if a survey was conducted 100 times with vineyard visitors, feedback received would be within a percentage division, either higher or lower than the percentage that accounted for 93 out of 100 times.
In this case, if 60 visitors report that the wines were extremely good. As the margin of error is plus or minus 5% in a confidence interval is 93%, in 100 visitors, it’s safe to conclude that the visitors who comment that the wines were “extremely good” will be 55 or 65 (93%) of the time.
To explain this further, let’s take an example of a survey on volunteering that was sent to 1000 respondents, out of which 500 agreed to the statement in the survey saying that volunteering makes life better. Calculate the margin of error for a 95% confidence level.
Step 1: Calculate p̂ by dividing the number of respondents who agreed with the statement in the survey by the total number of respondents. In this case, = 500/1000 = 50%
Step 2: Find the z-score corresponding to a 95% confidence level. In this case, the z score is 1.96
Step 3: Calculate by putting these values in the formula
Step 4: Convert to a percentage
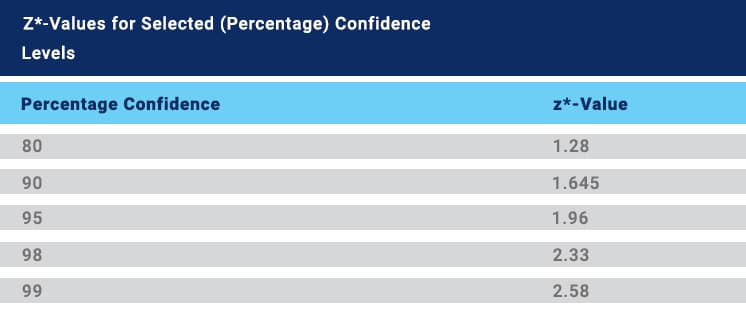
The Margin of Error in Sample Sizes
In probability sampling, each member of a population has a probability of being selected to be a part of the sample. Researchers and statisticians can select members in this method from their area of research so that the margin of error in data received from these samples is as minimal as possible.
In non-probability sampling, samples are formed based on cost-effectiveness or convenience and not on the basis of application and because of this selection process, some sections of the population may get excluded. Surveys will be effective only in filtering members according to interests and application to the survey being conducted.
The industrial standard for confidence level is 95%, and these are the margin of error percentages for certain survey sample sizes:
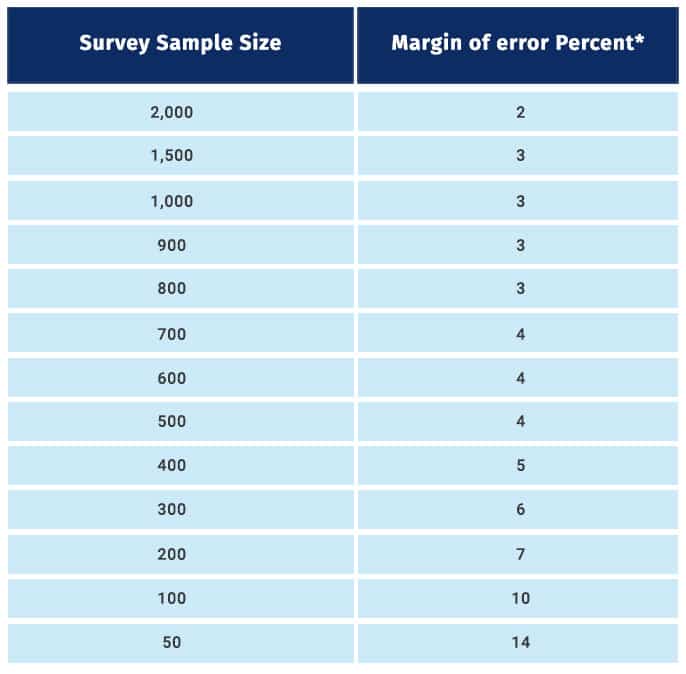
As indicated in this table, to reduce the margin of error to half, for instance, from 4 to 2, the sample size determination has been increased considerably, from 500 to 2000. As you must have observed, the sample size is inversely proportional to it. Till sample sizes of 1500, there is a significant decrease in it, but beyond that, this decrease reduces.
Why is the Margin of Error Important?
The margin of error is important because it helps us understand how much trust we can put in a survey or poll results. It shows the level of uncertainty in the data, and without it, we might think the results are more accurate than they really are. Here’s why it matters:
1. Gives Context to Results:
The margin of error helps us see that no survey is 100% perfect. For example, if a poll says 60% of people like a product, but the margin of error is ±3%, the true number could be anywhere from 57% to 63%. This gives us a clearer picture of the possible range of opinions.
2. Helps in Decision-Making:
People often use polls to make decisions—whether it’s a company launching a product or a politician running for office. Knowing the margin of error helps decision-makers understand the reliability of the data and avoid making mistakes based on false assumptions.
3. Shows How Reliable the Data Is:
A smaller margin of error means the survey is likely more reliable, while a larger margin of error suggests more uncertainty. This helps us decide how much confidence we should have in the results.
4. Avoids Misinterpretation:
Without considering the margin of error, we might believe the survey results are completely accurate when they might not be. For instance, a poll showing a 51% to 49% result in favor of one candidate could be within the margin of error, meaning the race is actually too close to call.
Applications and Case Studies of Margin of Error in Research
The margin of error is used in many types of research to give us a clearer picture of the data. It helps researchers and decision-makers understand how much uncertainty is in the results. Here are some examples and case studies where the margin of error is applied:
1. Political Polls
Political polling is one of the most common areas where the margin of error comes into play. Before an election, polling organizations survey a sample of voters to predict who will win. For example, if a poll shows that 52% of voters support one candidate and the margin of error is ±3%, this means the true support could be anywhere between 49% and 55%. If the margin of error is large, the race might be closer than it appears, and the poll results could change depending on who was surveyed.
In the 2016 U.S. presidential election, many polls predicted that Hillary Clinton would win. Some of these polls had a margin of error of around ±3%. This means the actual outcome could have been slightly different, and it’s one reason why some of the predictions were off.
2. Market Research
Companies often use surveys to find out how consumers feel about their products. If a company is testing a new product, it may survey a sample of people to see how popular the product is. Let’s say the survey finds that 70% of people like the product, but the margin of error is ±5%. This means the true approval rating could be anywhere from 65% to 75%. The company can then decide how to move forward, knowing that there is some uncertainty in the result.
A smartphone company might conduct a survey asking people if they like a new feature. If 80% of people say yes, but the error margin is ±4%, the company knows that the true percentage points of satisfaction could be 76% to 84%. This helps the company understand how strong the support for the new feature really is before they make any big decisions.
3. Health Research
In health research, the margin of error is often used when studying things like the effectiveness of a new drug or medical treatment. Researchers might test a drug on a sample of patients, and if they find that 70% of patients improved, but the margin of error is ±2%, the true improvement rate could be between 68% and 72%. This helps doctors and researchers be more cautious in interpreting the results and making recommendations.
A clinical trial for a new vaccine shows that 90% of participants were protected from a virus, but the margin of error is ±3%. This means the true effectiveness rate could be as low as 87% or as high as 93%. Health officials need to consider this margin of error before making policy decisions or recommending widespread use of the vaccine.
4. Social Science Studies
Researchers studying social behaviors, such as voting patterns or opinions on a social issue, often use the margin of error to show how much the results can vary. For example, a study might find that 65% of people support a certain law, but with a margin of error of ±4%, the actual support could range from 61% to 69%. This helps the researchers understand the level of confidence they can have in the study’s findings.
A study might look at public opinion about climate change. If 55% of people say they’re worried about it, but the margin of error is ±2%, the researchers know that the true level of concern could be anywhere between 53% and 57%. This is important for policymakers when making decisions based on public opinion.
Conclusion
The margin of error is an important tool that helps us understand the reliability and uncertainty of data. Whether it’s a political poll, a market survey, or a medical study, the margin of error provides context for interpreting results. It tells us that no survey or study is perfect, and the true outcome might be slightly different from what’s reported.
By considering the margin of error, we can make more informed decisions and avoid drawing conclusions that might be misleading. So, next time you read a poll or research result, remember to look at the margin of error to get the full picture!
Ready to take your research game to the next level? To enhance the quality of your research, consider joining QuestionPro today. With its customizable templates and advanced analytics, you can easily create professional-grade surveys that provide valuable insights. So, don’t miss out on the fun. Join QuestionPro today for free and start discovering what your customers, employees, and communities really think. No credit card is needed.
Frequently Asked Questions (FAQs)
A 10% margin of error is acceptable for low-stakes or exploratory research but too high for critical decisions or precise studies. For better accuracy, aim for a margin of error of 5% or less by increasing the sample size.
The margin of error for a 95% confidence interval depends on the sample size and sample proportion. It is calculated using the Margin of Error formula. Here, 1.96 is the z-score for a 95% confidence level. The exact value varies based on your data.
The confidence level represents the percentage of times the true population parameter would fall within the margin of error if the survey were repeated (e.g., 95% confidence level).
The margin of error indicates the range of possible values around the sample result that likely contains the true population value.
In short, the confidence level shows how certain you are, while the margin of error shows how much variation is expected.







