Regressieanalyse is misschien wel een van de meest gebruikte statistische methoden om de relatie tussen een reeks onafhankelijke en afhankelijke variabelen te onderzoeken of te schatten. Bij statistische analyse is het essentieel om onderscheid te maken tussen categorische gegevens en numerieke gegevens, omdat categorische gegevens verschillende categorieën of labels bevatten, terwijl numerieke gegevens bestaan uit meetbare grootheden.
Het wordt ook gebruikt als een algemene term voor verschillende gegevensanalysetechnieken die worden gebruikt in een kwalitatieve onderzoeksmethode voor het modelleren en analyseren van talrijke variabelen. Bij de regressiemethode is de afhankelijke variabele een voorspeller of een verklarend element, en de afhankelijke variabele is het resultaat of een antwoord op een specifieke vraag.
LEER OVER: Statistische analysemethoden
Definitie van regressieanalyse
Regressieanalyse wordt vaak gebruikt om gegevens te modelleren of te analyseren. De meeste onderzoeksanalisten gebruiken het om de relatie tussen de variabelen te begrijpen, die verder kan worden gebruikt om de precieze uitkomst te voorspellen.
Bijvoorbeeld – Stel dat een frisdrankbedrijf zijn productie-eenheid wil uitbreiden naar een nieuwere locatie. Voordat het bedrijf verder gaat, wil het zijn model voor het genereren van inkomsten analyseren en de verschillende factoren die hierop van invloed kunnen zijn. Daarom voert het bedrijf een online enquête uit met een specifieke vragenlijst.
Na het gebruik van regressieanalyse wordt het gemakkelijker voor het bedrijf om de enquêteresultaten te analyseren en de relatie tussen verschillende variabelen zoals elektriciteit en omzet te begrijpen – hier is omzet de afhankelijke variabele.
LEER OVER: Analyseniveau
Bovendien helpt inzicht in de relatie tussen verschillende onafhankelijke variabelen zoals prijsstelling, aantal werknemers en logistiek en de omzet het bedrijf om de impact van verschillende factoren op de omzet en winst in te schatten.
Onderzoekers gebruiken deze techniek vaak om de correlatie tussen verschillende variabelen te onderzoeken en te vinden. Het biedt de mogelijkheid om de invloed van verschillende onafhankelijke variabelen op een afhankelijke variabele te meten.
Over het algemeen bespaart regressieanalyse de onderzoekers van het onderzoek extra inspanningen bij het ordenen van verschillende onafhankelijke variabelen in tabellen en het testen of berekenen van hun effect op een afhankelijke variabele. Verschillende soorten analytische onderzoeksmethoden worden veel gebruikt om nieuwe bedrijfsideeën te evalueren en weloverwogen beslissingen te nemen.
Soorten regressieanalyse
Onderzoekers beginnen meestal met het leren van lineaire en logistische regressie. Door de wijdverspreide kennis van deze twee methoden en het gemak waarmee ze kunnen worden toegepast, denken veel analisten dat er maar twee soorten modellen zijn. Elk model heeft zijn eigen specialiteit en vermogen om te presteren als aan specifieke voorwaarden wordt voldaan.
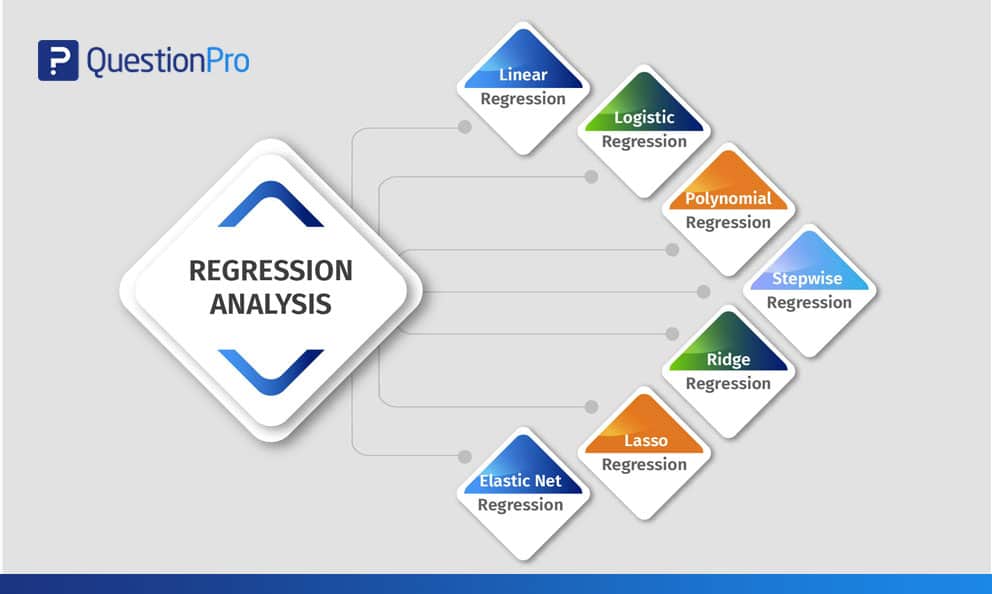
In deze blog worden de zeven veelgebruikte typen meervoudige regressieanalysemethoden uitgelegd die kunnen worden gebruikt om de getelde gegevens in verschillende formaten te interpreteren.
01. Lineaire regressieanalyse
Het is een van de meest bekende modelleringstechnieken, omdat het een van de eerste elite regressieanalysemethoden is die mensen oppikten bij het leren van voorspellend modelleren. Hier is de afhankelijke variabele continu en de onafhankelijke variabele is vaker continu of discreet met een lineaire regressielijn.
Houd er rekening mee dat meervoudige lineaire regressie meer dan één onafhankelijke variabele heeft dan eenvoudige lineaire regressie. Lineaire regressie kan dus het beste alleen worden gebruikt als er een lineair verband is tussen de onafhankelijke en een afhankelijke variabele.
Voorbeeld
Een bedrijf kan lineaire regressie gebruiken om de effectiviteit van marketingcampagnes, prijzen en promoties op de verkoop van een product te meten. Stel dat een bedrijf dat sportartikelen verkoopt, wil weten of het geld dat het heeft geïnvesteerd in de marketing en branding van zijn producten, al dan niet een substantieel rendement heeft opgeleverd.
Lineaire regressie is de beste statistische methode om de resultaten te interpreteren. Het beste aan lineaire regressie is dat het ook helpt bij het analyseren van de obscure impact van elke marketing- en merkactiviteit, waarbij het potentieel van de component om de verkoop te reguleren toch wordt gecontroleerd.
Als het bedrijf twee of meer reclamecampagnes tegelijkertijd uitvoert, één op televisie en twee op de radio, dan kan lineaire regressie eenvoudig de onafhankelijke en gecombineerde invloed van het samen uitvoeren van deze advertenties analyseren.
LEER OVER: Data Analytics Projecten
02. Logistische regressieanalyse
Logistische regressie wordt vaak gebruikt om de waarschijnlijkheid van slagen en falen van een gebeurtenis te bepalen. Logistische regressie wordt gebruikt wanneer de afhankelijke variabele binair is, zoals 0/1, Waar/Onwaar of Ja/Nee. Er kan dus gezegd worden dat logistische regressie gebruikt wordt om de gesloten vragen in een enquête te analyseren of de vragen die numerieke antwoorden vereisen in een enquête.
Logistische regressie vereist geen lineaire relatie tussen een afhankelijke en een onafhankelijke variabele, net als lineaire regressie. Logistische regressie past een niet-lineaire logtransformatie toe voor het voorspellen van de odds ratio; daarom kan het gemakkelijk verschillende soorten relaties tussen een afhankelijke en een onafhankelijke variabele aan.
Voorbeeld
Logistische regressie wordt veel gebruikt om categorische gegevens te analyseren, met name voor binaire responsgegevens bij het modelleren van bedrijfsgegevens. Vaker wordt logistische regressie gebruikt als de afhankelijke variabele categorisch is, bijvoorbeeld om te voorspellen of de gezondheidsclaim van een persoon echt(1) of frauduleus is, om te begrijpen of de tumor kwaadaardig(1) is of niet.
Bedrijven gebruiken logistische regressie om te voorspellen of consumenten in een bepaalde demografie hun product zullen kopen of bij de concurrent, op basis van leeftijd, inkomen, geslacht, ras, woonplaats, eerdere aankoop, enz.
03. Polynomiale regressieanalyse
Polynomiale regressie wordt vaak gebruikt om kromlijnige gegevens te analyseren als de macht van een onafhankelijke variabele meer dan 1 is. Bij deze regressieanalysemethode is de best passende lijn nooit een ‘rechte lijn’, maar altijd een ‘kromme lijn’ die in de gegevenspunten past.
Houd er rekening mee dat polynomiale regressie beter te gebruiken is als twee of meer variabelen exponenten hebben en een paar niet.
Bovendien kan het niet-lineair scheidbare gegevens modelleren en biedt het de vrijheid om de exacte exponent voor elke variabele te kiezen, en dat met volledige controle over de beschikbare modelleringsfuncties.
Voorbeeld
In combinatie met responsoppervlakteanalyse wordt polynomiale regressie beschouwd als een van de geavanceerde statistische methoden die vaak worden gebruikt in onderzoek naar feedback uit meerdere bronnen. Polynomiale regressie wordt meestal gebruikt in financiële en verzekeringsgerelateerde bedrijfstakken waar de relatie tussen afhankelijke en onafhankelijke variabelen kromlijnig is.
Stel dat iemand zijn uitgaven wil budgetteren door te bepalen hoe lang het zou duren om een definitief bedrag te verdienen. Polynomiale regressie kan, door rekening te houden met zijn/haar inkomen en uitgaven te voorspellen, eenvoudig bepalen hoeveel tijd hij/zij precies moet werken om dat specifieke bedrag te verdienen.
04. Stapsgewijze regressieanalyse
Dit is een semi-geautomatiseerd proces waarbij een statistisch model wordt opgebouwd door de afhankelijke variabele toe te voegen of te verwijderen op basis van de t-statistieken van hun geschatte coëfficiënten.
Als je de stapsgewijze regressie goed gebruikt, heb je krachtigere gegevens binnen handbereik dan welke methode ook. Het werkt goed als je werkt met een groot aantal onafhankelijke variabelen. Het verfijnt gewoon het model van de analyse-eenheid door willekeurig in variabelen te prikken.
Stapsgewijze regressieanalyse wordt aanbevolen als er meerdere onafhankelijke variabelen zijn, waarbij de selectie van onafhankelijke variabelen automatisch gebeurt zonder menselijke tussenkomst.
Let op: bij stapsgewijze regressiemodellering wordt de variabele toegevoegd aan of afgetrokken van de verzameling verklarende variabelen. De reeks toegevoegde of verwijderde variabelen wordt gekozen afhankelijk van de teststatistieken van de geschatte coëfficiënt.
Voorbeeld
Stel dat je een reeks onafhankelijke variabelen hebt zoals leeftijd, gewicht, lichaamsoppervlak, duur van hypertensie, basale hartslag en stressindex op basis waarvan je de invloed op de bloeddruk wilt analyseren.
Bij stapsgewijze regressie wordt automatisch de beste subset van de onafhankelijke variabele gekozen; het begint ofwel met het kiezen van geen enkele variabele om verder te gaan (door één variabele per keer toe te voegen) of het begint met alle variabelen in het model en gaat achteruit (door één variabele per keer te verwijderen).
Met behulp van regressieanalyse kun je dus de invloed van elke of een groep variabelen op de bloeddruk berekenen.
05. Nokregressieanalyse
Nokregressie is gebaseerd op een gewone kleinste-kwadratenmethode die wordt gebruikt om multicollineariteitgegevens te analyseren (gegevens waarbij onafhankelijke variabelen sterk gecorreleerd zijn). Collineariteit kan worden uitgelegd als een bijna-lineaire relatie tussen variabelen.
Als er sprake is van multicollineariteit, zullen de schattingen van de kleinste kwadraten onvertekend zijn, maar als het verschil tussen de schattingen groter is, kunnen ze ver verwijderd zijn van de werkelijke waarde. Nokregressie elimineert echter de standaardfouten door een zekere mate van vertekening toe te voegen aan de regressieschattingen met als doel betrouwbaardere schattingen te geven.
Als je wilt, kun je ook meer leren over Selection Bias via onze blog.
Let op: Veronderstellingen afgeleid uit de nokregressie zijn vergelijkbaar met de kleinste-kwadratenregressie, met als enige verschil de normaliteit. Hoewel de waarde van de coëfficiënt in de nokregressie beperkt is, bereikt deze nooit nul, wat duidt op het onvermogen om variabelen te selecteren.
Voorbeeld
Stel dat je gek bent op twee gitaristen die live optreden op een evenement bij jou in de buurt, en je gaat naar hun optreden kijken met het motief om uit te vinden wie een betere gitarist is. Maar als de voorstelling begint, merk je dat ze allebei tegelijkertijd zwart-blauwe noten spelen.
Is het mogelijk om de beste gitarist te vinden die de grootste invloed op het geluid heeft als ze allebei hard en snel spelen? Omdat ze allebei verschillende noten spelen, is het aanzienlijk moeilijk om ze van elkaar te onderscheiden, waardoor dit het beste geval van multicollineariteit is, waardoor de standaardfouten van de coëfficiënten toenemen.
Ridge regressie pakt multicollineariteit in dit soort gevallen aan en bevat bias of een krimpschatting om resultaten af te leiden.
06. Lasso-regressieanalyse
Lasso (Least Absolute Shrinkage and Selection Operator) is vergelijkbaar met nokregressie, maar gebruikt een absolute waarde bias in plaats van de kwadratische bias gebruikt in nokregressie.
Het werd al in 1989 ontwikkeld als een alternatief voor de traditionele kleinste-kwadraten-schatting met de bedoeling om de meeste problemen met betrekking tot overfitting op te lossen wanneer de gegevens een groot aantal onafhankelijke variabelen bevatten.
Lasso heeft de mogelijkheid om beide uit te voeren – variabelen selecteren en ze te regulariseren samen met een zachte drempel. Het toepassen van lasso-regressie maakt het eenvoudiger om een subset van voorspellers af te leiden uit het minimaliseren van voorspellingsfouten tijdens het analyseren van een kwantitatieve respons.
Merk op dat regressiecoëfficiënten die een nulwaarde bereiken na inkrimping worden uitgesloten van het lasso-model. Regressiecoëfficiënten met een waarde groter dan nul zijn daarentegen sterk geassocieerd met de responsvariabelen, waarbij de verklarende variabelen kwantitatief, categorisch of beide kunnen zijn.
Voorbeeld
Stel dat een autobedrijf een onderzoeksanalyse wil uitvoeren naar het gemiddelde brandstofverbruik van auto’s in de VS. Als voorbeelden kozen ze 32 automodellen en 10 kenmerken van auto-ontwerp – aantal cilinders, cilinderinhoud, bruto paardenkracht, achterasverhouding, gewicht, ¼ mijl tijd, v/s motor, transmissie, aantal versnellingen en aantal carburateurs.
Zoals je kunt zien is de correlatie tussen de responsvariabele mpg (miles per gallon) extreem gecorreleerd met enkele variabelen zoals gewicht, cilinderinhoud, aantal cilinders en paardenkracht. Het probleem kan worden geanalyseerd met behulp van het pakket glmnet in R en lassoregressie voor kenmerkselectie.
07. Elastische netregressieanalyse
Het is een mengsel van nok- en lasso-regressiemodellen getraind met L1- en L2-normen. Het elastische net zorgt voor een groeperingseffect waarbij sterk gecorreleerde voorspellers de neiging hebben om samen in of uit het model te gaan. Het gebruik van het elastische net regressiemodel wordt aanbevolen als het aantal voorspellers veel groter is dan het aantal waarnemingen.
Houd er rekening mee dat het elastic net regressiemodel is ontstaan als een optie voor het lasso regressiemodel omdat de variabele sectie van lasso te veel afhankelijk was van gegevens, waardoor het instabiel werd. Door gebruik te maken van elastische netregressie werden statistici in staat om de straffen van nok- en lassoregressie te overbruggen om zo het beste uit beide modellen te halen.
Voorbeeld
Een klinisch onderzoeksteam dat toegang had tot een microarray dataset over leukemie (LEU) was geïnteresseerd in het construeren van een diagnostische regel gebaseerd op het expressieniveau van gepresenteerde genmonsters om het type leukemie te voorspellen. De dataset die ze hadden, bestond uit een groot aantal genen en een paar monsters.
Daarnaast kregen ze een specifieke set monsters om te gebruiken als trainingsmonsters, waarvan sommige besmet waren met type 1 leukemie (acute lymfoblastische leukemie) en sommige met type 2 leukemie (acute myeloïde leukemie).
Model fitting en tuning parameterselectie door tienvoudige CV werden uitgevoerd op de trainingsgegevens. Daarna vergeleken ze de prestaties van die methoden door hun voorspellende gemiddelde-kwadraatfout te berekenen op de testgegevens om de nodige resultaten te krijgen.
Gebruik van regressieanalyse in marktonderzoek
Een marktonderzoek richt zich op drie belangrijke matrices: Klanttevredenheid, Klantloyaliteit en Customer Advocacy. Onthoud dat, hoewel deze matrices ons vertellen over de gezondheid en intenties van de klant, ze ons niet vertellen hoe we de positie kunnen verbeteren. Daarom is een diepgaande vragenlijst om consumenten te vragen naar de reden van hun ontevredenheid zeker een manier om praktische inzichten te krijgen.
Het is echter gebleken dat mensen vaak moeite hebben om hun motivatie of demotivatie naar voren te brengen of hun tevredenheid of ontevredenheid te beschrijven. Bovendien hechten mensen altijd te veel belang aan bepaalde rationele factoren, zoals prijs, verpakking, enz. In het algemeen fungeert het als een voorspellend analytisch en voorspellend hulpmiddel in marktonderzoek.
Bij gebruik als voorspellingshulpmiddel kan regressieanalyse de verkoopcijfers van een organisatie bepalen door rekening te houden met externe marktgegevens. Een multinational voert een marktonderzoek uit om inzicht te krijgen in de impact van verschillende factoren zoals BBP (Bruto Binnenlands Product), CPI (Consumenten Prijs Index) en andere soortgelijke factoren op zijn inkomstengeneratiemodel.
Uiteraard werd regressieanalyse met het oog op voorspelde marketingindicatoren gebruikt om een voorlopige omzet te voorspellen die in toekomstige kwartalen en zelfs in toekomstige jaren zal worden gegenereerd. Maar hoe verder je in de toekomst gaat, hoe onbetrouwbaarder de gegevens worden, waardoor er een grote foutmarge overblijft.
Casestudie over het gebruik van regressieanalyse
Een waterzuiveringsbedrijf wilde inzicht krijgen in de factoren die leidden tot merkvoorkeur. De enquête was het beste medium om bestaande en potentiële klanten te bereiken. Er werd een grootschalig consumentenonderzoek gepland en er werd een discrete vragenlijst opgesteld met behulp van het beste onderzoeksinstrument.
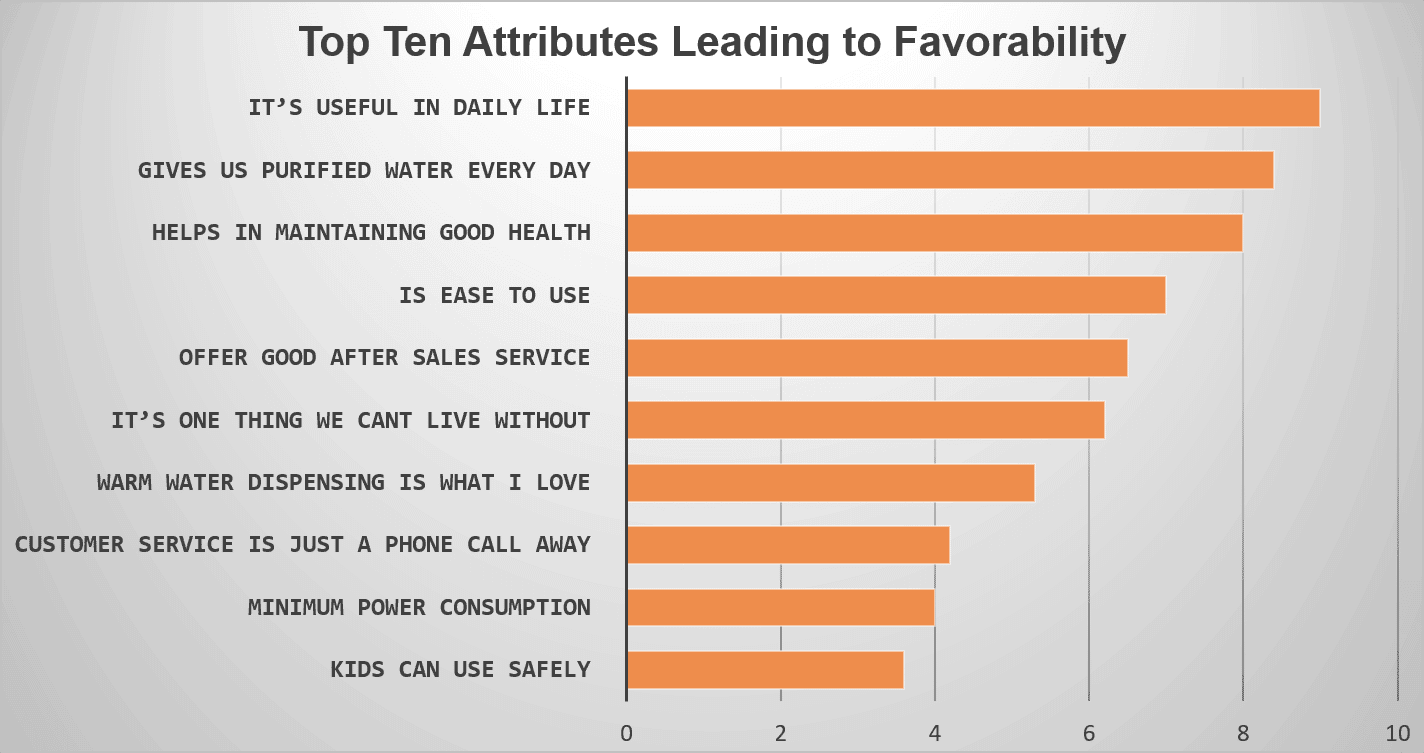
In de enquête werden effectief een aantal vragen gesteld over het merk, de voorkeur, de tevredenheid en de waarschijnlijke ontevredenheid. Na het verkrijgen van optimale antwoorden op de enquête werd regressieanalyse gebruikt om de top tien factoren te bepalen die verantwoordelijk zijn voor de merkvriendelijkheid.
Alle tien afgeleide kenmerken (vermeld in de afbeelding hieronder) benadrukten op de een of andere manier hun belang bij het beïnvloeden van de voorkeur voor dat specifieke waterzuiveringsmerk.
Hoe leidt regressieanalyse inzichten af uit enquêtes?
Het is gemakkelijk om een regressieanalyse uit te voeren met Excel of SPSS, maar als je dat doet, moet je het belang van vier getallen bij het interpreteren van de gegevens begrijpen.
De eerste twee van de vier getallen hebben direct betrekking op het regressiemodel zelf.
- F-waarde: Het helpt bij het meten van de statistische significantie van het onderzoeksmodel. Onthoud dat een F-waarde die significant lager is dan 0,05 als meer betekenisvol wordt beschouwd. Een F-waarde kleiner dan 0,05 garandeert dat de resultaten van de enquêteanalyse niet toevallig zijn.
- R-kwadraat: Dit is de waarde waarin de onafhankelijke variabelen de hoeveelheid beweging door afhankelijke variabelen proberen te verklaren. Als de R-kwadraatwaarde 0,7 is, kan een geteste onafhankelijke variabele 70% van de beweging van de afhankelijke variabele verklaren. Dit betekent dat de resultaten van de enquêteanalyse zeer voorspellend van aard zijn en als accuraat kunnen worden beschouwd.
De andere twee getallen hebben betrekking op elk van de onafhankelijke variabelen bij het interpreteren van de regressieanalyse.
- P-waarde: Net als de F-waarde is ook de P-waarde statistisch significant. Bovendien geeft het hier aan hoe relevant en statistisch significant het effect van de onafhankelijke variabele is. Nogmaals, we zoeken naar een waarde kleiner dan 0,05.
- Interpretatie: Het vierde getal heeft betrekking op de coëfficiënt die wordt bereikt na het meten van de impact van variabelen. We testen bijvoorbeeld meerdere onafhankelijke variabelen om een coëfficiënt te krijgen. Het vertelt ons ‘met welke waarde de afhankelijke variabele naar verwachting zal toenemen wanneer onafhankelijke variabelen (die we in beschouwing nemen) met één toenemen terwijl alle andere onafhankelijke variabelen op dezelfde waarde blijven.
In enkele gevallen wordt de eenvoudige coëfficiënt vervangen door een gestandaardiseerde coëfficiënt die de bijdrage van elke onafhankelijke variabele aan een verandering in de afhankelijke variabele laat zien.
Voordelen van het gebruik van regressieanalyse in een online enquête
01. Krijg toegang tot voorspellende analyses
Weet je dat het gebruik van regressieanalyse om de uitkomst van een bedrijfsenquête te begrijpen hetzelfde is als het vermogen om toekomstige kansen en risico’s te onthullen?
Na het zien van een bepaald reclameslot op televisie kunnen we bijvoorbeeld het exacte aantal bedrijven voorspellen door die gegevens te gebruiken om een maximaal bod voor dat slot in te schatten. De financiële en verzekeringssector als geheel is sterk afhankelijk van regressieanalyse van enquêtegegevens om trends en kansen te identificeren voor nauwkeurigere planning en besluitvorming.
02. Operationele efficiëntie verbeteren
Wist je dat bedrijven regressieanalyse gebruiken om hun bedrijfsprocessen te optimaliseren?
Voordat bedrijven bijvoorbeeld een nieuwe productlijn lanceren, voeren ze consumentenonderzoeken uit om de impact van verschillende factoren op de productie, verpakking, distributie en consumptie van het product beter te begrijpen.
Een datagestuurde prognose helpt het giswerk, de hypothese en de interne politiek uit de besluitvorming te halen. Een beter begrip van de gebieden die de operationele efficiëntie en inkomsten beïnvloeden, leidt tot een betere bedrijfsoptimalisatie.
03. Kwantitatieve ondersteuning voor besluitvorming
Bedrijfsenquêtes genereren tegenwoordig veel gegevens met betrekking tot financiën, inkomsten, bedrijfsvoering, aankopen, enz. en bedrijfseigenaren zijn sterk afhankelijk van verschillende modellen voor gegevensanalyse om weloverwogen zakelijke beslissingen te kunnen nemen.
Regressieanalyse helpt ondernemingen bijvoorbeeld om weloverwogen strategische beslissingen te nemen over hun personeelsbestand. Het uitvoeren en interpreteren van de resultaten van personeelsenquêtes zoals Employee Engagement Surveys, Employee Satisfaction Surveys, Employer Improvement Surveys, Employee Exit Surveys, enz. vergroot het inzicht in de relatie tussen werknemers en de onderneming.
Het helpt ook om een goed beeld te krijgen van bepaalde problemen die de werkcultuur, werkomgeving en productiviteit van de organisatie beïnvloeden. Bovendien reduceren intelligente bedrijfsgerichte interpretaties de enorme stapel ruwe gegevens tot bruikbare informatie om een beter geïnformeerde beslissing te nemen.
04. Fouten door intuïtie voorkomen
Als je weet hoe je regressieanalyse moet gebruiken om enquêteresultaten te interpreteren, kun je gemakkelijk feitelijke ondersteuning bieden aan het management om weloverwogen beslissingen te nemen. Maar weet je dat het ook helpt om fouten in het oordeel uit te sluiten?
Bijvoorbeeld, een manager van een winkelcentrum denkt dat als hij de sluitingstijd van het winkelcentrum verlengt, dat zal leiden tot meer verkoop. Regressieanalyse spreekt de overtuiging tegen dat het voorspellen van hogere inkomsten als gevolg van hogere verkoopcijfers de hogere bedrijfskosten als gevolg van langere werktijden niet zal ondersteunen.
Conclusie
Regressieanalyse is een nuttige statistische methode voor het modelleren en begrijpen van relaties tussen variabelen. Het biedt talloze voordelen voor verschillende gegevenstypes en interacties. Onderzoekers en analisten kunnen nuttige inzichten krijgen in de factoren die een afhankelijke variabele beïnvloeden en de resultaten gebruiken om weloverwogen beslissingen te nemen.
Met QuestionPro Research kunt u de efficiëntie en nauwkeurigheid van regressieanalyses verbeteren door de processen voor gegevensverzameling, analyse en rapportage te stroomlijnen. De gebruiksvriendelijke interface en het brede scala aan functies van het platform maken het een waardevol hulpmiddel voor onderzoekers en analisten die regressieanalyses uitvoeren als onderdeel van hun onderzoeksprojecten.
Meld je vandaag nog aan voor de gratis proefversie en laat je onderzoeksdromen de vrije loop!







