
Correlatie is een fundamenteel concept in statistiek en gegevensanalyse, dat helpt om de relatie tussen twee variabelen te begrijpen. Hoewel sterke positieve of negatieve correlaties vaak worden benadrukt, is nulcorrelatie even belangrijk.
Dit betekent dat er geen lineair verband is tussen de variabelen. Met andere woorden, veranderingen in de ene variabele voorspellen geen veranderingen in de andere.
In deze blog verkennen we het concept van nulcorrelatie, geven we een duidelijke definitie, illustratieve voorbeelden en methoden om het te bepalen.
Wat is een nulcorrelatie?
Nulcorrelatie is een statistische term die een situatie beschrijft waarin er geen lineair verband is tussen twee variabelen. Wanneer twee variabelen een correlatie van nul hebben, voorspellen veranderingen in de ene variabele geen veranderingen in de andere. De correlatiecoëfficiënt, die de mate en richting van de relatie tussen variabelen meet, is in dit geval precies nul.
Inzicht in deze correlatie is belangrijk bij statistische analyse omdat het helpt variabelen te identificeren die geen voorspellende relatie met elkaar hebben, wat cruciaal is bij het bouwen van statistische modellen of het interpreteren van gegevenspatronen.
Waarom is nulcorrelatie belangrijk?
Nulcorrelatie is om verschillende redenen een belangrijk concept in de statistiek en gegevensanalyse:
Het identificeert onafhankelijkheid
Het helpt om variabelen te identificeren die lineair onafhankelijk van elkaar zijn. Als twee variabelen een correlatie van nul hebben, geven veranderingen in de ene variabele geen informatie over veranderingen in de andere. Dit is cruciaal voor het begrijpen van de structuur van de gegevens en de relaties (of het gebrek daaraan) tussen variabelen.
Het verbetert statistische modellen
In regressieanalyse en andere statistische modellen kan het opnemen van variabelen met deze correlatie met de afhankelijke variabele ruis toevoegen en de voorspellende kracht van het model verminderen. Door dergelijke variabelen te identificeren en uit te sluiten, kunnen modellen worden vereenvoudigd en efficiënter worden gemaakt, wat leidt tot betere prestaties en betere interpreteerbaarheid.
Deze correlatie helpt verkeerde interpretaties voorkomen
Inzicht in deze correlatie voorkomt een verkeerde interpretatie van gegevens.
- Een onderzoeker kan bijvoorbeeld ten onrechte een verband tussen twee variabelen afleiden op basis van intuïtie of eerste waarnemingen.
Het berekenen van de correlatiecoëfficiënt en het vinden van een nulcoëfficiënt maakt duidelijk dat er geen lineair verband bestaat, waardoor onjuiste conclusies worden vermeden.
Het benadrukt niet-lineaire relaties
Het benadrukt de mogelijkheid van niet-lineaire relaties. Als twee variabelen geen correlatie hebben, hoeft dat niet te betekenen dat ze niet gerelateerd zijn; ze kunnen een complexe, niet-lineaire relatie hebben. Als je dit herkent, kan dit leiden tot verder onderzoek met andere methoden, zoals niet-lineaire regressie of gegevenstransformaties.
Correlatie helpt bij het sturen van experimenteel ontwerp
Bij het ontwerpen van experimenten kan weten welke variabelen nul correlatie hebben een leidraad zijn bij het selecteren van variabelen die moeten worden meegenomen of waarvoor moet worden gecontroleerd. Dit helpt bij het ontwerpen van robuustere experimenten waarbij de invloed van irrelevante variabelen wordt geminimaliseerd, wat leidt tot duidelijkere, betrouwbaardere resultaten.
Het begrijpt variabel gedrag
Het geeft inzicht in het gedrag van variabelen in een dataset. In financiële analyse kan inzicht in welke activa geen correlatie met elkaar hebben helpen bij portefeuillediversificatie, omdat het combineren van dergelijke activa het totale risico kan verlagen.
Het ondersteunt hypothesetests
Bij hypothesetests is deze correlatie vaak een nulhypothese.
- Bij het testen of twee variabelen aan elkaar gerelateerd zijn, kan de nulhypothese bijvoorbeeld stellen dat de correlatie tussen deze variabelen nul is.
Vaststellen of dit waar of onwaar is, helpt bij het valideren of weerleggen van hypotheses.
Wat zijn de voorbeelden van nulcorrelatie?
Voorbeelden van deze correlatie, waarbij veranderingen in de ene variabele niet overeenkomen met veranderingen in een andere variabele, zijn te vinden op verschillende gebieden, zoals:
Onderzoeksgebied
Voorbeeld: Aantal wetenschappelijke publicaties en favoriete ijssmaak
Een studie onderzoekt de relatie tussen het aantal wetenschappelijke publicaties van een onderzoeker en hun favoriete ijssmaak.
Er is geen logisch verband tussen het aantal wetenschappelijke artikelen dat een onderzoeker publiceert en zijn voorkeur voor een bepaalde ijssmaak. Daarom wordt verwacht dat deze twee variabelen deze correlatie zullen vertonen.
Onderwijs
Voorbeeld: De schoenmaat van leerlingen en hun cijfers voor wiskunde
In een onderwijsstudie wordt onderzocht of er een verband is tussen de schoenmaat van leerlingen en hun cijfers voor wiskunde.
Schoenmaat is een fysiek kenmerk dat geen invloed heeft op de schoolprestaties van een leerling in wiskunde. Daarom is de correlatie tussen schoenmaat en wiskundecijfers waarschijnlijk nul.
Gezondheidszorg
Voorbeeld: Bloedgroep en incidentie van verkoudheid
In een studie in de gezondheidszorg wordt onderzocht of er een verband bestaat tussen iemands bloedgroep en het aantal keren dat iemand een verkoudheid oploopt in een jaar.
Bloedgroep is niet geassocieerd met de frequentie van verkoudheid, die wordt beïnvloed door verschillende andere factoren zoals blootstelling aan virussen en de sterkte van het immuunsysteem. Daarom is de correlatie tussen bloedgroep en de incidentie van verkoudheid naar verwachting nul.
Hoe identificeer je nulcorrelatie?
Hier zullen we onderzoeken hoe we deze correlatie kunnen identificeren door visuele inspectie, statistische berekening, hypothesetests en contextuele analyse.
1. Visuele inspectie met behulp van spreidingsdiagrammen
Scatterplots zijn een effectief hulpmiddel om de relatie tussen twee variabelen visueel te beoordelen.
Een spreidingsdiagram maken:
- Plaats een variabele op de x-as en de andere op de y-as.
- Zoek naar een waarneembare trend of patroon in de gegevenspunten.
Correlatie vaststellen:
- Als de punten willekeurig verspreid zijn zonder duidelijke trend (noch opwaarts noch neerwaarts), suggereert dit correlatie.
- Een willekeurige spreiding houdt in dat geen enkele lijn (recht of gebogen) goed bij de gegevenspunten past.
Voorbeeld:
- Schoenmaten van leerlingen versus wiskundecijfers: Als je schoenmaten uitzet tegen wiskundecijfers en je ziet een willekeurige puntenwolk zonder trend, dan wijst dit op een correlatie van nul.
2. Bereken de correlatiecoëfficiënt
De Pearson correlatiecoëfficiënt (r) is de meest gebruikelijke maat voor lineaire correlatie.
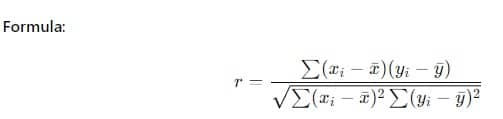
Stappen:
- Verzamel gepaarde gegevenspunten voor de twee variabelen.
- Zoek het gemiddelde van elke variabele.
- Bereken hoe ver elk gegevenspunt van het gemiddelde af ligt.
- Vermenigvuldig de afwijkingen voor elk paar en tel de producten bij elkaar op.
- Gebruik de formule om de correlatiecoëfficiënt te vinden.
Correlatie interpreteren:
Waarde dicht bij 0: Als 𝑟 r dicht bij 0 ligt, duidt dit op weinig tot geen lineaire relatie tussen de variabelen.
Voorbeeld:
- Schoenmaten en wiskundecijfers: Als de berekende𝑟 ongeveer 0 is, bevestigt dit een correlatie van nul.
3. De hypothese testen
Statistische hypothesetests kunnen bepalen of een waargenomen correlatiecoëfficiënt significant verschilt van nul.
Stappen:
- Nulhypothese: Neem aan dat de correlatiecoëfficiënt nul is.
- Alternatieve hypothese: Neem aan dat de correlatiecoëfficiënt niet nul is.
- Bereken de teststatistiek: Gebruik een t-test voor de correlatiecoëfficiënt.
- Bepaal de p-waarde: Vergelijk de p-waarde met een significantieniveau (bijv. 0,05).
Nul correlatie:
- Als de p-waarde groter is dan het significantieniveau, verwerp dan de nulhypothese niet, wat suggereert dat de correlatie niet significant verschilt van nul.
Voorbeeld:
- Bloedgroep en incidentie van verkoudheid: Als de p-waarde hoog is, geeft dit aan dat de waargenomen correlatie statistisch niet significant is en dat er geen correlatie is.
4. Contextuele analyse begrijpen
Inzicht in de context en theoretische achtergrond van de variabelen is essentieel voor het interpreteren van correlatieresultaten.
Stappen:
- Onderzoek variabelen: Bekijk de aard en de verwachte relaties tussen de variabelen.
- Domeinkennis toepassen: Gebruik kennis uit het vakgebied om te veronderstellen of een relatie verwacht wordt.
Nul correlatie:
- Als de theorie en eerder onderzoek suggereren dat er geen logische relatie is, ondersteunt dit de bevinding van deze correlatie.
Voorbeeld:
- Bloedgroep en incidentie van verkoudheid: De wetenschap dat bloedgroep geen invloed heeft op de vatbaarheid voor verkoudheid ondersteunt de interpretatie van nul correlatie als die gevonden wordt.
Negatieve vs Positieve Correlatie vs Nul Correlatie
Correlatie is een statistische maat die de sterkte en richting van de relatie tussen twee variabelen beschrijft. Hier volgt een gedetailleerde uitleg van negatieve, positieve en nulcorrelatie:
Positieve correlatie
- Definitie: Een positieve correlatie treedt op wanneer twee variabelen in dezelfde richting bewegen. Als de ene variabele stijgt, stijgt de andere ook, en als de ene daalt, daalt de andere ook.
- Voorbeeld: De relatie tussen lengte en gewicht. Over het algemeen neemt iemands gewicht toe naarmate hij langer wordt.
- Grafische weergave: In een scatterplot hebben punten de neiging zich te groeperen rond een lijn die van links naar rechts omhoog loopt.
Negatieve correlatie
- Definitie: Een negatieve correlatie treedt op wanneer twee variabelen in tegengestelde richtingen bewegen. Als de ene variabele toeneemt, neemt de andere variabele af, en omgekeerd.
- Voorbeeld: De relatie tussen de hoeveelheid tijd die je besteedt aan studeren en het aantal fouten dat je maakt op een toets. Over het algemeen neemt het aantal fouten af naarmate er meer tijd aan studeren wordt besteed.
- Grafische weergave: In een scatterplot clusteren de punten rond een lijn die van links naar rechts naar beneden helt.
Nul correlatie
- Definitie: Het geeft aan dat er geen relatie is tussen de twee variabelen. Veranderingen in de ene variabele voorspellen geen veranderingen in de andere variabele.
- Voorbeeld: De relatie tussen de schoenmaat van een persoon en zijn intelligentiequotiënt (IQ). Er is geen logisch verband tussen deze twee variabelen.
- Grafische weergave: In een scatter plot zijn de punten willekeurig verdeeld zonder waarneembaar patroon of helling.
Hoe kan QuestionPro helpen bij correlatieanalyse?
QuestionPro, een robuust enquêteplatform, biedt uitgebreide tools om correlatieanalyses effectief uit te voeren. Hier ziet u hoe QuestionPro u kan helpen bij het uitvoeren van correlatieanalyses:
Moeiteloze gegevensverzameling
QuestionPro vereenvoudigt het gegevensverzamelingsproces met zijn gebruiksvriendelijke tools voor het maken van enquêtes. U kunt enquêtes ontwerpen en verspreiden om kwantitatieve gegevens te verzamelen over verschillende variabelen van belang. Het platform ondersteunt verschillende vraagtypen, zodat u op efficiënte wijze gedetailleerde en relevante gegevens kunt vastleggen.
Geautomatiseerde gegevensanalyse
Zodra de gegevens zijn verzameld, biedt QuestionPro ingebouwde analysehulpmiddelen voor correlatieanalyse. U kunt eenvoudig correlaties berekenen, die de sterkte en richting van de lineaire relatie tussen twee variabelen meten. De lineaire correlatiecoëfficiënt loopt van -1 tot 1, waarbij:
- 1 geeft een perfect positieve correlatie aan.
- -1 geeft een perfect negatieve correlatie aan.
- 0 geeft aan dat er geen correlatie is.
Visuele weergave
QuestionPro biedt visualisatiehulpmiddelen om u te helpen de resultaten van uw correlatieanalyse te interpreteren. Scatterplots en correlatiematrices kunnen worden gegenereerd voor een duidelijke grafische weergave van de relaties tussen variabelen. Dit visuele hulpmiddel is cruciaal voor het snel identificeren van trends en patronen.
Patronen en trends identificeren
Met behulp van de correlatieanalyse van QuestionPro observeerden onderzoekers correlaties (positief, negatief of nul) tussen variabelen:
- Positieve correlatie: Beide variabelen bewegen in dezelfde richting. Meer reclame-uitgaven kunnen bijvoorbeeld correleren met meer verkoop.
- Negatieve correlatie: De variabelen neigen in tegengestelde richting te bewegen. Bijvoorbeeld, meer schermtijd kan correleren met verminderde schoolprestaties.
- Nul correlatie: Er bestaat geen verband tussen de variabelen. Bijvoorbeeld, het aantal jaren op school kan niet correleren met het aantal letters in iemands naam.
Praktische toepassingen
Correlatieanalyse in QuestionPro kan worden gebruikt voor verschillende praktische toepassingen, zoals:
- Marktonderzoek: Meet de effectiviteit van marketingcampagnes door reclame-uitgaven te correleren met verkoopprestaties.
- Gezondheidszorg: Beoordeel de relatie tussen medicijngebruik en patiëntresultaten, zoals bloeddrukniveaus.
- Onderwijs: Bepaal de impact van studiegewoonten op academische prestaties door studie-uren te correleren met cijfers.
Conclusie
Nul correlatie tussen twee variabelen betekent de afwezigheid van een lineair verband, wat aangeeft dat veranderingen in de ene variabele niet corresponderen met veranderingen in de andere. Door correlatiecoëfficiënten te berekenen en gegevens te visualiseren door middel van scatterplots, kunnen onderzoekers nauwkeurig bepalen of variabelen gecorreleerd zijn, positief gecorreleerd zijn, negatief gecorreleerd zijn of deze correlatie vertonen.
Het gebruik van QuestionPro voor correlatieanalyse in uw enquêtes biedt een krachtige manier om zinvolle relaties tussen variabelen bloot te leggen. Door gebruik te maken van de intuïtieve interface, geavanceerde analytische tools en uitgebreide rapportagefuncties van QuestionPro kunt u op efficiënte wijze correlatieanalyses uitvoeren en waardevolle inzichten uit uw gegevens halen. Neem vandaag nog contact op met QuestionPro voor meer informatie!







