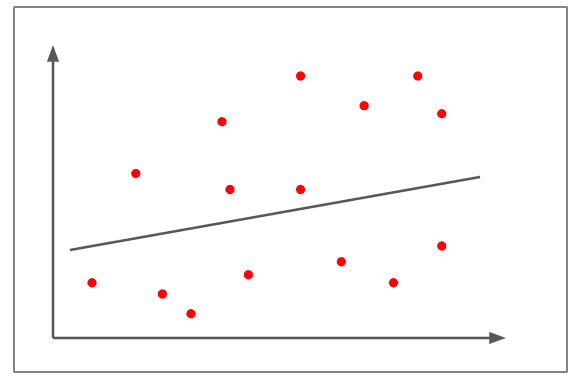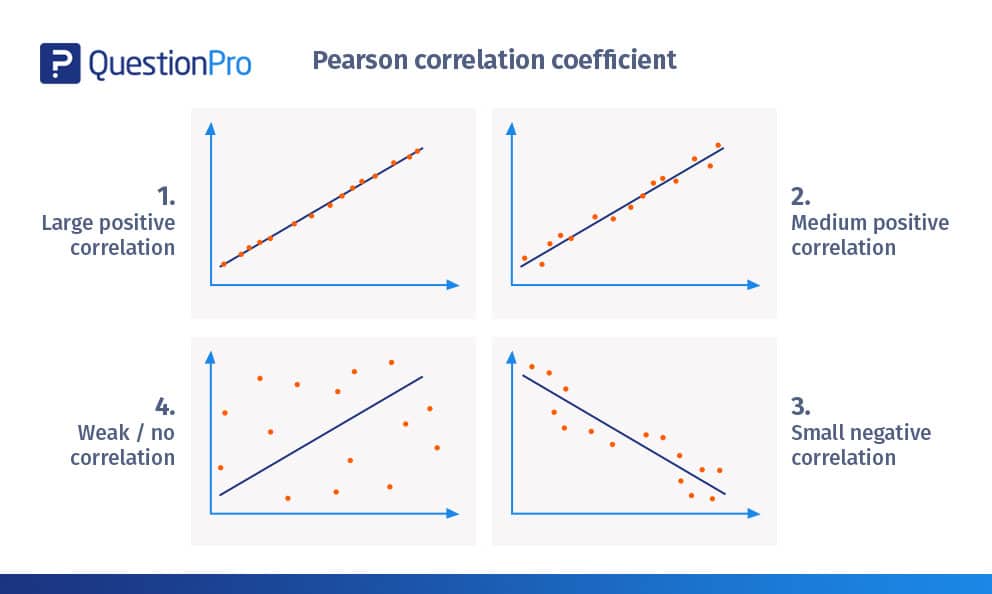
Het is gebruikelijk om lineaire relaties te kwantificeren door middel van de Pearson correlatiecoëfficiënt. Om de sterkte en richting van het verband tussen twee variabelen aan te geven, neemt het een waarde aan tussen -1 en 1.
Het kan beleggers helpen diversifiëren. Berekeningen van scatterplots van historische rendementen tussen paren van activa, zoals aandelen-obligaties, aandelen-grondstoffen, obligaties-vastgoed, enz., zullen beleggers helpen bij het samenstellen van risico-rendementportefeuilles.
Daarom zullen we leren over de correlatiecoëfficiënt van Pearson en weten hoe we hiermee de relatie tussen twee gerelateerde variabelen kunnen meten.
Wat is de correlatiecoëfficiënt van Pearson?
Pearson correlatiecoëfficiënt of Pearson’s correlatiecoëfficiënt of Pearson’s r wordt in de statistiek gedefinieerd als de meting van de sterkte van de relatie tussen twee variabelen en hun verband met elkaar.
Eenvoudig gezegd berekent de correlatiecoëfficiënt van Pearson het effect van een verandering in de ene variabele wanneer de andere variabele verandert.
Bijvoorbeeld: Tot een bepaalde leeftijd (in de meeste gevallen) zal de lengte van een kind blijven toenemen naarmate zijn/haar leeftijd toeneemt. Natuurlijk is zijn/haar groei afhankelijk van verschillende factoren zoals genen, locatie, dieet, levensstijl, enz.
Deze benadering is gebaseerd op covariantie en is daarom de beste methode om de relatie tussen twee variabelen te meten.
Wat doet de Pearson correlatiecoëfficiënttest?
De correlatie van de Pearson coëfficiënt heeft een hoge statistische significantie. Er wordt gekeken naar de relatie tussen twee variabelen. Het probeert een lijn te trekken door de gegevens van twee variabelen om hun relatie aan te tonen. De relatie tussen de variabelen wordt gemeten met behulp van de Pearson correlatiecoëfficiënt calculator. Deze lineaire relatie kan positief of negatief zijn.
Bijvoorbeeld:
- Positief lineair verband: In de meeste gevallen, universeel, neemt het inkomen van een persoon toe naarmate zijn/haar leeftijd stijgt.
- Negatief lineair verband: Als het voertuig zijn snelheid verhoogt, neemt de reistijd af en omgekeerd.
Uit het bovenstaande voorbeeld blijkt duidelijk dat de correlatiecoëfficiënt van Pearson, r, twee dingen probeert te achterhalen – de sterkte en de richting van de relatie op basis van de gegeven steekproefomvang.
Formule en berekening van de correlatiecoëfficiënt van Pearson
De correlatiecoëfficiëntformule achterhaalt het verband tussen de variabelen. Het retourneert de waarden tussen -1 en 1. Gebruik de onderstaande Pearson coëfficiënt correlatie calculator om de sterkte van twee variabelen te meten.
Formule voor de correlatiecoëfficiënt van Pearson:
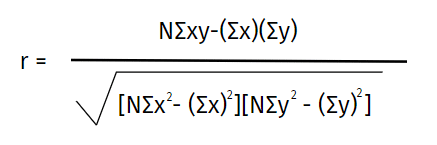
Waar:
N = het aantal paren scores
Σxy = de som van de producten van gepaarde scores
Σx = de som van x scores
Σy = de som van y scores
Σx2 = de som van de gekwadrateerde x-scores
Σy2 = de som van de gekwadrateerde y-scores
Berekening
Hier volgt een stapsgewijze handleiding voor het berekenen van de correlatiecoëfficiënt van Pearson:
Stap één: Maak een tabel met correlatiecoëfficiënten.
Maak een gegevensgrafiek met beide variabelen. Label deze variabelen ‘x’ en ‘y’. Voeg drie extra kolommen toe – (xy), (x^2) en (y^2). Raadpleeg deze eenvoudige grafiek.

Stap twee: Gebruik basisvermenigvuldiging om de tabel aan te vullen.

Stap drie: Tel alle kolommen van onder naar boven op.
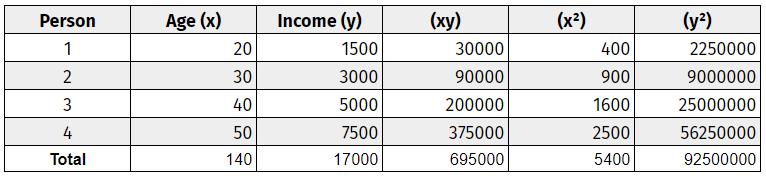
Stap vier: Gebruik de correlatieformule om de waarden in te pluggen.
Als het resultaat negatief is, is er een negatieve correlatie tussen de twee variabelen. Als het resultaat positief is, is er een positieve correlatie tussen de variabelen. Resultaten kunnen ook de sterkte van een lineaire relatie definiëren, d.w.z. sterke positieve relatie, sterke negatieve relatie, gemiddelde positieve relatie, enzovoort.
De sterkte van de Pearson product-moment correlatiecoëfficiënt bepalen
De Pearson product-moment correlatiecoëfficiënt, of gewoon de Pearson correlatiecoëfficiënt of de Pearson correlatiecoëfficiënt r, bepaalt de sterkte van de lineaire relatie tussen twee variabelen.
Hoe sterker de associatie tussen de twee variabelen, hoe meer je antwoord naar 1 of -1 neigt. Het bereiken van waarden van 1 of -1 betekent dat alle gegevenspunten op de rechte lijn van ‘best fit’ worden uitgezet. Dit betekent dat de verandering in factoren van een variabele de correlatie met de andere variabele niet verzwakt. Hoe dichter je antwoord bij 0 ligt, hoe meer variatie er in de variabelen zit.
Hoe de Pearson correlatiecoëfficiënt interpreteren
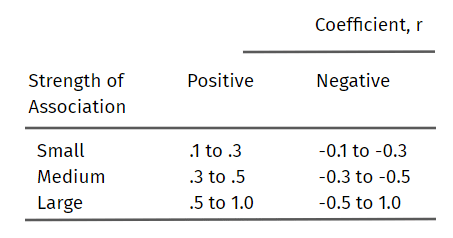
Hieronder volgen de voorgestelde richtlijnen voor de interpretatie van de Pearson coëfficiënt correlatie:
Merk op dat de sterkte van de associatie van de variabelen afhangt van wat je meet en de steekproefgrootte.
Op een grafiek kun je de relatie tussen de variabelen zien en aannames doen voordat je ze zelfs maar berekent. Als de scatterplots dicht bij de lijn liggen, tonen ze een sterke relatie tussen de variabelen.
Hoe dichter de scatterplots bij de lijn liggen, hoe sterker de relatie tussen de variabelen. Hoe verder ze van de lijn af bewegen, hoe zwakker de relatie wordt. Als de lijn bijna evenwijdig is aan de x-as doordat de scatterplots willekeurig op de grafiek zijn geplaatst, is het veilig om aan te nemen dat er geen correlatie is tussen de twee variabelen.
Wat betekenen de termen kracht en richting?
De termen ‘sterkte’ en ‘richting’ hebben statistische betekenis. Hier volgt een eenvoudige uitleg van de twee woorden:
- Sterkte: Sterkte geeft de correlatie aan tussen twee variabelen. Het betekent hoe consistent de ene variabele zal veranderen door de verandering in de andere. Waarden die dicht bij +1 of -1 liggen duiden op een sterke relatie. Deze waarden worden bereikt als de gegevenspunten op of heel dicht bij de lijn vallen.
Hoe verder de gegevenspunten uit elkaar liggen, hoe zwakker de sterkte van de lineaire relatie. Als er geen praktische manier is om een rechte lijn te trekken omdat de gegevenspunten verspreid liggen, is de sterkte van de lineaire relatie het zwakst. - Richting: De richting van de lijn geeft een positieve lineaire of negatieve lineaire relatie tussen variabelen aan. Als de lijn een opwaartse helling heeft, hebben de variabelen een positieve relatie.
Dit betekent dat een toename in de waarde van de ene variabele zal leiden tot een toename in de waarde van de andere variabele. Een negatieve correlatie wijst op een neerwaartse helling. Dit betekent dat een toename in de hoeveelheid van één variabele leidt tot een afname in de waarde van een andere variabele.
Voorbeelden van Pearson correlatiecoëfficiënt
Laten we eens kijken naar enkele visuele voorbeelden om je te helpen de correlatiecoëfficiëntentabel te interpreteren:
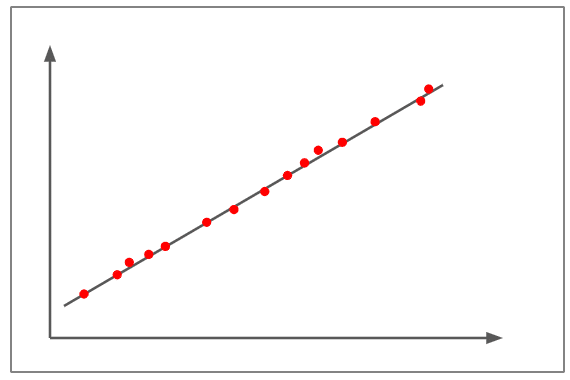
Grote positieve correlatie
- De bovenstaande figuur toont een correlatie van bijna +1.
- De scatterplots zijn bijna in een rechte lijn uitgezet.
- De helling is positief, wat betekent dat als de ene variabele toeneemt, de andere variabele ook toeneemt, wat een positieve lineaire lijn laat zien.
- Dit betekent dat een verandering in de ene variabele recht evenredig is met de verandering in de andere variabele.
- Een voorbeeld van een grote positieve correlatie zou zijn – Als kinderen groeien, groeien ook hun kleding- en schoenmaten.
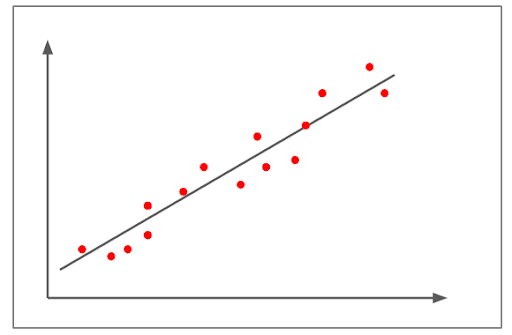
Gemiddelde positieve correlatie
- De bovenstaande figuur laat een positieve correlatie zien.
- De correlatie is hoger dan +0,8 maar lager dan 1+.
- Het laat een vrij sterk lineair bergopwaarts patroon zien.
- Een voorbeeld van een gemiddelde positieve correlatie zou zijn – Als het aantal auto’s toeneemt, neemt ook de vraag naar de variabele brandstof toe.
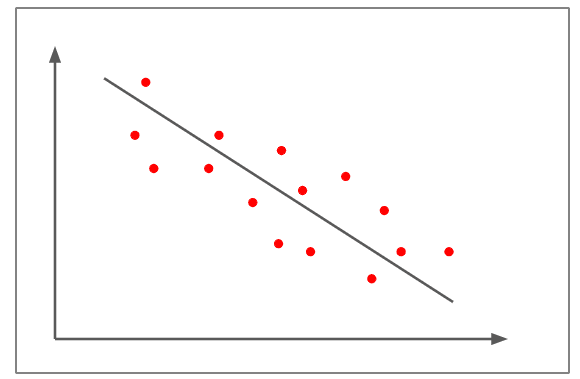
Kleine negatieve correlatie
- In de bovenstaande figuur liggen de scatterplots niet zo dicht bij de rechte lijn als in de eerdere voorbeelden.
- Het vertoont een negatieve lineaire correlatie van ongeveer -0,5
- De verandering in de ene variabele is omgekeerd evenredig met de verandering in de andere variabele, omdat de helling negatief is.
- Een voorbeeld van een kleine negatieve correlatie zou zijn – Hoe meer iemand eet, hoe minder honger hij heeft.
Zwakke / geen correlatie
- De scatterplots liggen ver van de lijn.
- Het is moeilijk om praktisch een lijn te trekken.
- De correlatie is ongeveer +0,15
- Het kan niet worden beoordeeld of de verandering in de ene variabele recht evenredig of omgekeerd evenredig is met de andere variabele.
- Een voorbeeld van een zwakke/geen correlatie zou zijn – Een stijging in brandstofprijzen leidt ertoe dat minder mensen huisdieren adopteren.
Conclusie
De correlatiecoëfficiënt van Pearson kan worden bepaald door via een enquête gegevens te verzamelen over twee variabelen die van belang zijn. Je kunt dit gebruiken om te zien of de correlatie tussen de twee variabelen positief of negatief is en hoe sterk die is.
QuestionPro Research Suite is een suite met tools voor het benutten van onderzoek en het transformeren van inzichten die kunnen worden gebruikt om gegevens te verzamelen voor Pearson correlatiecoëfficiëntanalyse. Nadat u de enquêtegegevens uit QuestionPro hebt geëxporteerd en geïmporteerd in een spreadsheet of statistische toepassing, kunt u de correlatieanalyse uitvoeren.
QuestionPro biedt handige hulpmiddelen voor gegevensanalyse, zoals kruistabellen, gegevensvisualisatie en statistische tests, naast het berekenen van de correlatiecoëfficiënt. Deze kwaliteiten kunnen helpen bij je onderzoek en het begrijpen van de onderlinge relaties tussen je variabelen.
Klaar om de relatie tussen je variabelen te ontdekken en je gegevensanalyse te verbeteren? Start vandaag nog een gratis proefversie van QuestionPro om te zien hoe onze enquêtesoftware u kan helpen bij het eenvoudig bepalen van de Pearson correlatiecoëfficiënt. Mis deze kans niet om gegevensanalyse en onderzoek te verbeteren.