
A análise de regressão é talvez a técnica estatística mais utilizada para investigar ou estimar a relação entre variáveis dependentes e um conjunto de variáveis explicativas independentes.
Este tipo de análise de dados também é usado como um termo genérico para uma variedade de técnicas de análise de dados empregadas em métodos de pesquisa qualitativa para modelar e analisar inúmeras variáveis.
No método de regressão, a variável dependente é o resultado ou resposta a uma consulta específica, enquanto a variável independente é o preditor ou elemento explicativo. Vamos aprender mais sobre as características desta técnica de análise.
O que é uma análise de regressão?
A análise de regressão é um método estatístico que permite examinar a relação entre duas ou mais variáveis e identificar quais delas têm maior impacto sobre um tema de interesse.
Este tipo de análise estatística permite a classificação matemática por meio de diferentes questões, como: Quais fatores são mais importantes? Que fatores podem ser ignorados? Como esses fatores interagem entre si? E, finalmente, quão confiante você está em relação a todos esses fatores?
O processo de realização de uma regressão permite determinar com segurança quais fatores são mais importantes, quais podem ser ignorados e como eles influenciam uns aos outros. Esses fatores são chamados de variáveis e são classificadas como:
- Variável(is) dependente(s): É o fator mais importante que você está tentando compreender ou prever.
- Variáveis independentes: São os fatores que você acredita que podem impactar sua variável dependente.
Usos da análise de regressão
Um estudo de mercado é conduzido com foco em três matrizes principais: satisfação do cliente, fidelização do cliente e defesa do cliente. Deve-se ter em mente que, embora essas matrizes nos forneçam informações sobre a saúde e as intenções dos clientes, elas não indicam como melhorar a posição da empresa.
Portanto, numa pesquisa, perguntar aos consumidores sobre os motivos de sua insatisfação é, sem dúvida, uma forma de obter informações práticas.
No entanto, está comprovado que muitas vezes as pessoas têm dificuldade em expressar sua motivação ou desmotivação, ou em descrever sua satisfação ou insatisfação.
Além disso, as pessoas frequentemente atribuem importância excessiva a alguns fatores racionais, como preço e embalagem. Em geral, a análise de regressão atua como uma ferramenta de análise preditiva e previsão em pesquisas de mercado.
Quando usada como ferramenta de previsão, a análise de regressão pode ajudar a determinar os números de vendas de uma organização, levando em consideração dados de mercado externo.
Por exemplo, uma empresa multinacional realiza um estudo de mercado para entender o impacto de diversos fatores, como PIB (Produto Interno Bruto), IPC (Índice de Preços ao Consumidor) e outros indicadores semelhantes em seu modelo de geração de receita.
A análise de regressão, considerando os indicadores de marketing esperados, foi usada para prever uma receita provisória a ser gerada nos próximos trimestres e até mesmo nos anos futuros. No entanto, quanto mais avançamos no futuro, menos confiáveis são os dados, e isso deixa uma ampla margem de erro.
Exemplo: Uma empresa de purificadores de água queria entender os fatores que favorecem a marca. A pesquisa foi a melhor forma de alcançar clientes atuais e potenciais. Foi planejado um inquérito em grande escala, e um questionário detalhado foi preparado utilizando a melhor ferramenta de pesquisa disponível.
A pesquisa fez diversas perguntas relacionadas à marca, favorabilidade, satisfação e provável insatisfação. Depois de obter as respostas da pesquisa, a análise de regressão foi utilizada para identificar os dez principais fatores responsáveis pela favorabilidade da marca.
Todos os atributos identificados destacaram sua importância no impacto sobre a preferência pela marca específica de purificadores de água.
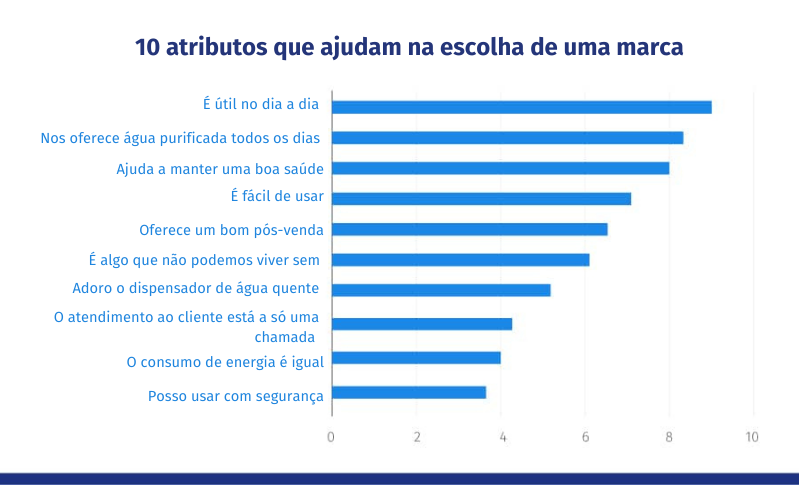
Como a análise de regressão permite obter informações de pesquisas
É fácil realizar análises de regressão com Excel ou SPSS, mas é necessário compreender a importância de quatro números na interpretação dos dados.
Os dois primeiros números estão diretamente relacionados ao próprio modelo de regressão:
- Valor F: Ajuda a medir a significância estatística do modelo de pesquisa. Um valor F significativamente menor que 0,05 é considerado mais significativo. Um valor F inferior a 0,05 garante que os resultados da análise não sejam aleatórios.
- R-Quadrado: Indica o grau em que a variável independente explica a variação na variável dependente. Se o valor de R-quadrado for 0,7, isso significa que 70% da variação da variável dependente pode ser explicada pela variável independente testada. Isso sugere que o resultado da análise é altamente preditivo e pode ser considerado preciso.
Os outros dois números referem-se a cada uma das variáveis independentes na interpretação da análise de regressão:
- Valor P: Assim como o valor F, o valor P também tem grande significância estatística. Indica a relevância e a significância estatística do efeito da variável independente. Buscamos um valor P inferior a 0,05.
- Coeficiente: Refere-se ao impacto das variáveis independentes na variável dependente. Por exemplo, ao testar múltiplas variáveis independentes, o coeficiente nos diz “quanto se espera que a variável dependente aumente quando as variáveis independentes (consideradas) aumentam em uma unidade, enquanto todas as outras variáveis independentes permanecem constantes.” Em alguns casos, o coeficiente simples é substituído por um coeficiente padronizado, que demonstra a contribuição de cada variável independente para a mudança na variável dependente.
Tipos de análise de regressão
Os diferentes tipos de análise de regressão são os seguintes:
Modelo de regressão linear simples
A regressão linear simples é a técnica mais utilizada para modelar a relação entre dois conjuntos de variáveis. O resultado é uma equação que pode ser usada para fazer projeções ou estimativas sobre os dados.
Neste modelo, há uma variável preditora (x) e uma variável dependente ou de resposta (Y). Imagine que a verdadeira relação entre Y e x é uma linha reta e que a observação Y em cada nível de x é uma variável aleatória.
O modelo de regressão linear simples caracteriza-se por prever a variável dependente através da seguinte equação:
E(Y/x) = 0 + β 1 x
Onde o intercepto β 0 e a inclinação β 1 são coeficientes de regressão desconhecidos.
Algumas dicas que você pode levar em consideração ao usar o modelo de regressão linear simples são:
- Você deve ter cuidado ao selecionar as variáveis com as quais as equações de regressão são construídas e determinar a forma do modelo.
- As relações de regressão são válidas apenas para valores de regressores que estão dentro do intervalo dos dados originais.
Modelo de regressão linear múltipla
A regressão linear múltipla é uma técnica estatística responsável por analisar situações que envolvem mais de uma variável.
Este método permite identificar quais variáveis independentes são aquelas que podem explicar uma variável independente, verificar as causas e prever aproximadamente os valores.
O modelo de regressão linear múltipla pode ser descrito a partir da seguinte equação:
Y = 0 + β 1 X 1 + β 2 X 2 +… + β n X n + ε
Onde Y é uma variável dependente, β representa seus estimadores e ε representa o resíduo ou erro.
Modelo de regressão não linear
A regressão não linear é um processo mais complicado onde pode ocorrer que o número de parâmetros não corresponda ao número de variáveis explicativas.
Um exemplo de modelo não linear nos parâmetros seria dado pela seguinte função exponencial:
Υ = αΧβ
Em muitos casos, as variáveis originais podem ser transformadas para converter a função não linear em linear e assim aplicar estas técnicas. Portanto, se a não linearidade afetar apenas as variáveis explicativas, mas não os coeficientes, novas variáveis poderão ser definidas.
Vantagens de usar análise de regressão em uma pesquisa online
Aqui estão alguns dos benefícios de realizar análise de regressão:

Você obtém acesso a análises preditivas
Você sabia que usar a análise de regressão para entender o resultado de uma pesquisa é como ter o poder de descobrir oportunidades e riscos futuros?
Por exemplo, após assistir a um determinado espaço publicitário na televisão, podemos prever o número exato de empresas que utilizarão esses dados para estimar um lance máximo para esse espaço.
O setor financeiro e de seguros, como um todo, depende fortemente da análise de regressão dos dados dos inquéritos para identificar tendências e oportunidades que permitem um planejamento e uma tomada de decisão mais precisos.
Melhore a eficiência operacional
Você sabia que as empresas utilizam a análise de regressão para otimizar seus processos de negócios?
Por exemplo, antes de lançar uma nova linha de produtos, as empresas realizam inquéritos aos consumidores com o objetivo de compreender melhor o impacto de vários fatores na produção, embalagem, distribuição e consumo desse produto.
Uma previsão baseada em dados ajuda a eliminar suposições e políticas internas da tomada de decisões. Uma compreensão mais profunda das áreas que afetam a eficiência operacional e as receitas leva a uma melhor otimização dos negócios.
Apoio quantitativo para tomada de decisão
Os estudos empresariais hoje geram uma enorme quantidade de dados relacionados a finanças, receitas, operações, compras, etc., e os proprietários de empresas dependem fortemente de vários modelos de análise de dados para tomar decisões de negócios informadas.
Por exemplo, a análise de regressão ajuda as empresas a tomar decisões estratégicas sobre pessoal. A realização e interpretação dos resultados de pesquisas com funcionários aumentam a compreensão do relacionamento entre os funcionários e a empresa.
Além disso, ajuda a obter uma visão justa de questões que podem afetar a cultura de trabalho, o ambiente e a produtividade da organização.
Com interpretações inteligentes orientadas para os negócios, a enorme pilha de dados brutos é reduzida a informações acionáveis para uma tomada de decisão mais informada.
Você evita erros baseados na intuição
Ao saber como usar a análise de regressão para interpretar os resultados da pesquisa, você pode fornecer suporte à administração na tomada de decisões informadas. Mas você sabia que também ajuda a evitar erros de julgamento?
Por exemplo, o gestor de um centro comercial pode acreditar que ampliar o horário de funcionamento resultará em mais vendas. A análise de regressão pode contradizer essa crença ao prever que o aumento da receita devido ao aumento das vendas não será suficiente para cobrir o aumento das despesas decorrentes do prolongamento do horário de funcionamento.
Importância da análise de regressão
A análise de regressão é fundamental para uma organização, pois permite determinar o grau em que as variáveis independentes influenciam as variáveis dependentes. Além disso, ela possibilita explicar fenômenos, prever tendências futuras e obter informações comerciais valiosas e acionáveis.
Este método fornece insights sobre a organização dos custos e como as funções das variáveis podem impactar o produto.
Realizar análises de regressão permitirá que você tome decisões de negócios mais informadas e eficientes, além de desenvolver estratégias para melhorar a qualidade de seus produtos e serviços, o que, por sua vez, beneficiará a receita de sua organização.
Descubra insights valiosos para seu negócio com a QuestionPro. Experimente nossa plataforma de pesquisa e veja como ela pode transformar seus dados em decisões estratégicas!



