O coeficiente de correlação de Spearman é uma medida não paramétrica da correlação de postos (dependência estatística do ranking entre duas variáveis). É usado principalmente para análise de dados. Aqui vamos explicar tudo sobre o tema!
O que é um coeficiente de correlação de Spearman?
O coeficiente de correlação de Spearman (ou rho de Spearman) é uma medida estatística utilizada para avaliar a força e direção da relação entre duas variáveis ordinais ou contínuas, sem exigir que as variáveis sigam uma distribuição normal.
Ele é baseado no ranking das observações, ao invés de seus valores absolutos, o que torna o coeficiente de Spearman uma alternativa útil ao coeficiente de correlação de Pearson, especialmente quando as variáveis não são lineares ou não atendem aos pressupostos de normalidade.
Antes de falar sobre a correlação de Spearman, é importante entender a correlação de Pearson, que é uma medida estatística da força de uma relação linear entre dados emparelhados.
Para o teste de cálculo e significância da variável de classificação, é necessário que as seguintes suposições de dados sejam verdadeiras:
- Nível de intervalo ou razão
- Relacionamento linear
- Bivariada distribuída
Se os seus dados não atenderem às suposições anteriores, você precisará do coeficiente de correlação de Spearman. Para isso, é necessário saber qual é a função monótona para compreendê-lo.
Uma função monótona é aquela que nunca diminui ou nunca aumenta, já que é um aumento variável independente. Pode ser explicado usando a imagem abaixo:
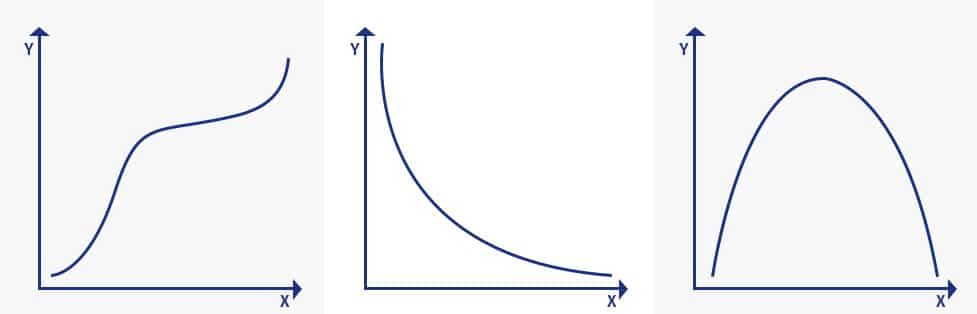
A imagem explica três conceitos da função monótona:
- Monotonicamente crescente: quando a variável “x” aumenta e a variável “y” nunca diminui.
- Diminui monotonicamente: quando a variável “x” aumenta, mas a variável “y” nunca aumenta.
- Não monótono: quando a variável “x” aumenta e a variável “e” às vezes aumenta e às vezes diminui.
A relação monótona é menos restritiva quando comparada a uma relação linear que é usada no coeficiente de correlação de Pearson. Embora a monotonicidade não seja o último requisito, não será significativo segui-la sem realmente determinar a força e a direção de uma relação monótona, se já se sabia que a relação entre a variável não é monótona.
Como calcular o coeficiente de correlação de Spearman
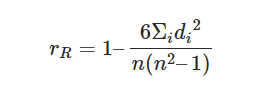
n = número de pontos de dados das duas variáveis
di = diferença de alcance do elemento “n”
O Coeficiente de Spearman, ⍴, pode ter um valor entre +1 e -1 onde,
Um valor de +1 em ⍴ significa uma associação de classificação perfeita Valor de 0 em ⍴ significa que não há associação de classificação Um valor de -1 em ⍴ significa uma associação negativa perfeita entre os intervalos.
Se o valor de ⍴ se aproxima de 0, a associação entre os dois intervalos é mais fraca.
Devemos ser capazes de classificar os dados antes de prosseguir com o coeficiente de correlação de Spearman. É importante notar que, se uma variável aumenta, a outra segue uma relação monótona.
Como o coeficiente de correlação de Spearman é usado
Em cada nível, você deve comparar os valores das duas variáveis. Aqui está um exemplo de como os cálculos funcionam:
Os resultados de 9 alunos em História e Geografia são mencionados na tabela a seguir.
Etapa 1: Crie uma tabela com os dados obtidos.
Etapa 2: Comece classificando os dois conjuntos de dados. A classificação dos dados pode ser obtida atribuindo a classificação “1” ao maior número da coluna, “2” ao segundo maior número e assim por diante. O menor valor geralmente terá a classificação mais baixa. Isso deve ser feito para os dois conjuntos de medidas.
Etapa 3: Adicione uma terceira coluna “d” ao seu conjunto de dados, “d” aqui indica a diferença entre os intervalos. Por exemplo, se o intervalo de física do primeiro aluno for 3 e o intervalo de matemática for 5, a diferença no intervalo será 3. Na quarta coluna, faça um quadrado com os valores “d”.
Etapa 4: Adicione todos os valores do quadrado “d” que é 12 (Σd quadrado).
Etapa 5: Insira esses valores na fórmula.
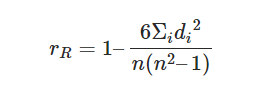
=1-(6*12)/(9(81-1))
=1-72/720
=1-01
=0.9
O coeficiente de correlação de Spearman para esses dados é 0,9 e, como mencionado acima, se o valor de ⍴ se aproxima de +1, então eles têm uma associação de classificação perfeita.
Vantagens da correlação de Spearman
A correlação de Spearman oferece várias vantagens em comparação com outros métodos de correlação, como o coeficiente de correlação de Pearson, especialmente quando as condições para este último não são atendidas. Aqui estão algumas das principais vantagens do coeficiente de correlação de Spearman:
1. Adequado para dados ordinais
- O coeficiente de Spearman é ideal para dados ordinais, onde as variáveis podem ser classificadas, mas as diferenças entre as classificações não são constantes ou mensuráveis. Exemplos incluem classificações em competições, níveis de satisfação (como de 1 a 5), e classificações de preferência.
2. Robustez frente a outliers
- Como a correlação de Spearman é baseada em ranks (posições relativas das observações), ela é menos sensível a outliers em comparação com o coeficiente de correlação de Pearson, que é baseado nos valores absolutos das variáveis. Outliers extremos não distorcem tanto os resultados.
3. Não exige normalidade dos dados
- Ao contrário do coeficiente de Pearson, que pressupõe que as variáveis seguem uma distribuição normal, o coeficiente de Spearman pode ser utilizado com dados não paramétricos, ou seja, dados que não precisam seguir uma distribuição específica, como normalidade ou linearidade.
4. Detecta relações monotônicas
- A correlação de Spearman mede relações monotônicas (ou seja, quando as variáveis se movem na mesma direção de forma consistente, mas não necessariamente de maneira linear). Isso é útil quando as variáveis aumentam ou diminuem juntas, mas não seguem uma linha reta, como ocorre em algumas relações causais ou fenômenos naturais.
5. Flexibilidade para dados contínuos e discretos
- Embora o coeficiente de Spearman seja frequentemente utilizado para dados ordinais, ele também pode ser usado para dados contínuos que não são linearmente relacionados. Ele pode, por exemplo, identificar relações não-lineares entre duas variáveis contínuas.
6. Interpretação simples e direta
- O coeficiente de Spearman tem uma interpretação simples, onde valores próximos de +1 ou -1 indicam correlações fortes e valores próximos de 0 indicam nenhuma correlação. Isso facilita a compreensão e comunicação dos resultados.
7. Aplicabilidade em diversos contextos
- A correlação de Spearman é amplamente usada em diversos campos, incluindo ciências sociais, biológicas, de saúde, e econômicas, quando há necessidade de analisar relações não lineares ou não paramétricas.
8. Independente da escala dos dados
- Como a análise é feita com base em ranks, a correlação de Spearman não se importa com a escala das variáveis. Isso significa que, mesmo que as variáveis tenham unidades ou intervalos diferentes, a correlação ainda pode ser calculada corretamente.
Como realizar o coeficiente de correlação de Spearman com a QuestionPro
Nesta seção, você aprenderá como executar o coeficiente de correlação de Spearman em sua pesquisa on-line.
Etapa 1: Vá para Minhas Pesquisas → Selecione o questionário → Análise
2: clique na análise de correlação
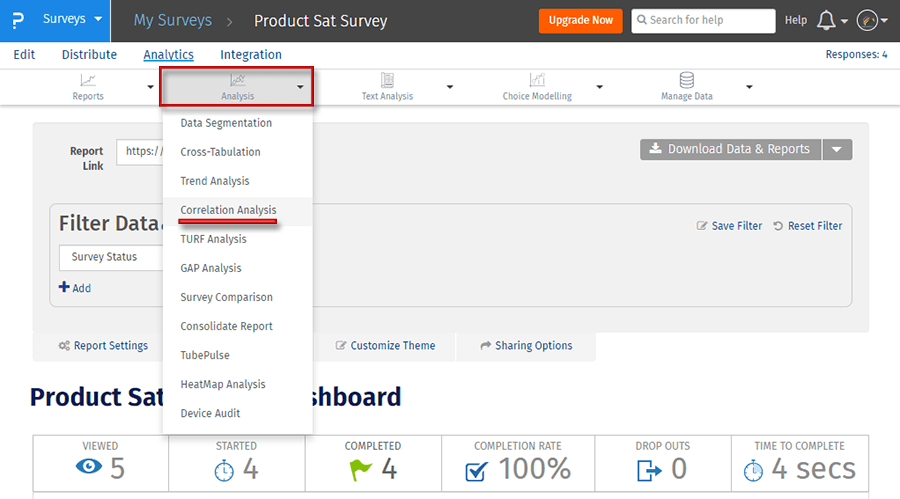
Etapa 3: Clique no botão Gerar coeficiente de Spearman para obter um relatório detalhado.
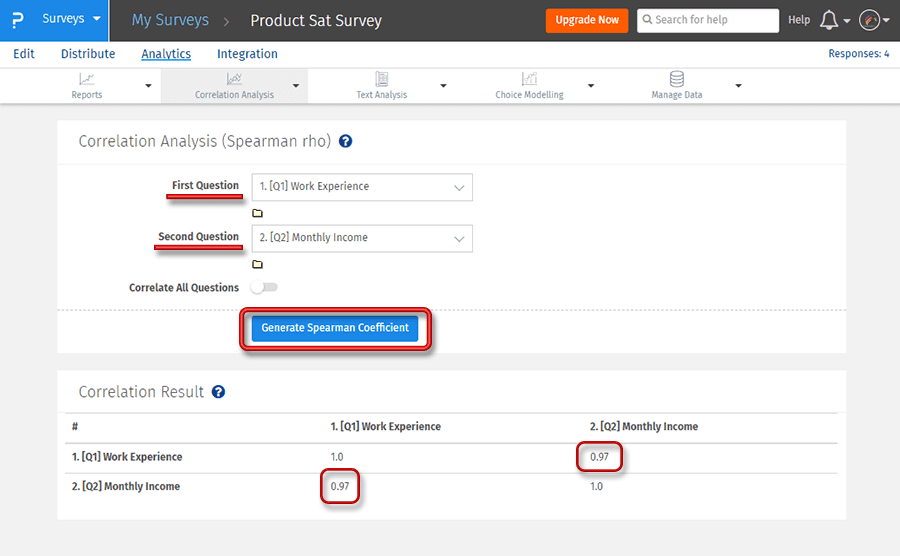
No exemplo anterior, o coeficiente de correlação de Spearman é usado para descobrir a relação entre as duas variáveis, experiência de trabalho e renda mensal. Uma ideia geral é que a renda mensal deve aumentar com a experiência de trabalho, o que significa que deve haver uma associação positiva entre as duas variáveis, o que é demonstrado pelo valor de rs que é 0,97.
Se você quiser usar esta ou outras funções da nossa plataforma para um projeto de pesquisa, não hesite em entrar em contato com um de nossos especialistas.
Para agilizar seu processo de trabalho e para que tenha recursos que enriquecem seu projeto de pesquisa, utilize uma plataforma online de pesquisa, te convido a conhecer a QuestionPro, uma solução completa em pesquisa e inteligência de mercado.
Siga-nos nas redes sociais e receba sempre dicas e novidades: Facebook, Twitter, Linkedin, Instagram