
O coeficiente de correlação de Pearson é um teste que mede a relação estatística entre duas variáveis contínuas. Se a associação entre os elementos não for linear, o coeficiente não será representado adequadamente.
O coeficiente de correlação de Pearson pode ter um intervalo de valores de +1 a -1. Um valor de 0 indica que não há associação entre as duas variáveis. Um valor maior que 0 indica uma associação positiva. Isto é, à medida que o valor de uma variável aumenta, o mesmo acontece com o valor da outra variável. Um valor menor que 0 indica uma associação negativa. Isto é, à medida que o valor de uma variável aumenta, o valor da outra diminui.
Para realizar a correlação de Pearson, é necessário cumprir o seguinte:
- A escala de medição deve ser uma escala ou relação de intervalo;
- As variáveis devem ser aproximadamente distribuídas;
- A associação deve ser linear;
- Não deve haver valores atípicos nos dados.
Veja e aprenda: Termos estatísticos utilizados em relatórios
Como o coeficiente de Correlação de Pearson é calculado
A fórmula do coeficiente de correlação de Pearson é a seguinte:
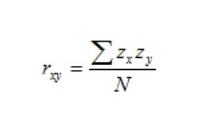
Imagem: Fórmula de Correlação de Pearson
Onde:
- “X” é igual à variável número um
- “Y” pertence à variável número dois
- “ZX” é o desvio padrão da variável um
- “ZY” é o desvio padrão da variável dois
- “N” é número de dados.
Interpretação do coeficiente
O coeficiente de correlação de Pearson tem o objetivo de indicar como as duas variáveis associadas estão entre si, assim:
- Correlação menor que zero: se a correlação é menor que zero, significa que é negativo, isto é, que as variáveis são inversamente relacionadas. Quando o valor de alguma variável é alto, o valor da outra variável é baixo. Quanto mais próximo você estiver de -1, mais clara será a covariação extrema. Se o coeficiente é igual a -1, nos referimos a uma correlação negativa perfeita.
- Correlação maior que zero: se a correlação for igual a +1, significa que é perfeito positivo. Neste caso, significa que a correlação é positiva, isto é, que as variáveis estão diretamente correlacionadas. Quando o valor de uma variável é alto, o valor da outra variável também é alto, o mesmo acontece quando eles são baixos. Se estiver próximo de +1, o coeficiente será covariado.
- Correlação igual a zero: Quando a correlação é igual a zero, significa que não é possível determinar qualquer senso de covariação. No entanto, isso não significa que não haja relação não linear entre as variáveis. Quando as variáveis são independentes, significa que elas estão correlacionadas, mas isso significa que o resultado é verdadeiro.
Leia também: Melhores Práticas para fazer pesquisa de mercado
Vantagens e desvantagens do coeficiente de correlação de Pearson
Entre as principais vantagens estão:
- O valor é independente de qualquer unidade usada para medir as variáveis.
- Se a amostra for grande, a precisão da estimativa é mais provável.
Algumas das desvantagens são:
- É necessário que as duas variáveis sejam medidas em um nível quantitativo contínuo.
- A distribuição das variáveis deve ser semelhante à curva normal.
Aplicação da Correlação de Pearson em diferentes áreas
A Correlação de Pearson é uma medida amplamente utilizada em diversas áreas do conhecimento, como a psicologia, medicina, economia e engenharia. A seguir, alguns exemplos de sua aplicação nessas áreas:
Psicologia
A correlação de Pearson é utilizada para avaliar a relação entre variáveis psicológicas, como a relação entre o desempenho em um teste de inteligência e o desempenho em uma tarefa de memória. Também é utilizada para investigar a relação entre comportamentos e características psicológicas, como a relação entre a ansiedade e a frequência de comportamentos compulsivos.
Confira: Dicas para um teste de personalidade online
Medicina
Na medicina, a correlação de Pearson é utilizada para avaliar a relação entre variáveis clínicas, como a relação entre a pressão arterial e o risco de doenças cardiovasculares. Além disso, é utilizada para avaliar a eficácia de tratamentos, como por exemplo, a relação entre a dosagem de um medicamento e a melhora dos sintomas de uma doença.
Leia também: Como elaborar uma pesquisa de satisfação do paciente?
Economia
Na economia, a correlação de Pearson é utilizada para avaliar a relação entre variáveis econômicas, como a relação entre o nível de emprego e o crescimento econômico. É possível aplicá-la para avaliar a relação entre variáveis financeiras, como a relação entre o preço das ações e o desempenho de uma empresa.
Engenharia
Na engenharia, a correlação de Pearson é utilizada para avaliar a relação entre variáveis técnicas, como a relação entre a temperatura e a pressão em um processo industrial. Também é possível avaliar a relação entre variáveis físicas, como a relação entre a resistência de um material e sua capacidade de suportar cargas mecânicas.
Conheça outros tipos de correlações
A Correlação de Pearson é uma das medidas mais comuns de correlação utilizadas na análise de dados, mas não é a única. Outras medidas de correlação incluem a correlação de Spearman, a correlação de Kendall e a correlação de ponto bisserial.
Correlação de Spearman
A correlação de Spearman é uma medida de correlação não paramétrica que avalia a relação monotônica entre duas variáveis, ou seja, não assume que as variáveis estão distribuídas normalmente. É comumente usada quando as variáveis apresentam uma relação não-linear ou quando há presença de outliers.
Aprenda mais: Saiba do que se trata coeficiente de correlação de Spearman
Correlação de Kendall
Assim como a de Spearman, também é uma medida de correlação não paramétrica, que avalia a relação monotônica entre duas variáveis. É especialmente útil quando há dados categóricos ou ordinais.
Correlação de ponto bisserial
A correlação de ponto bisserial é uma medida de correlação bivariada que avalia a relação entre uma variável contínua e uma variável dicotômica (binária). É comumente usada em pesquisas que avaliam a relação entre variáveis psicológicas e de saúde.
É importante considerar qual medida de correlação é mais adequada para uma determinada análise, levando em conta a natureza das variáveis, a distribuição dos dados e o objetivo da análise. Cada medida de correlação tem suas vantagens e limitações, e a escolha da medida mais apropriada pode ajudar a garantir uma análise mais precisa e confiável.




