
Na estatística, o desvio médio é uma importante medida que nos permite compreender o quanto os dados variam em relação a uma média definida.
É uma ferramenta fundamental para analisar e compreender conjuntos de dados em diversas disciplinas, como economia, psicologia, medicina e muitas outras.
Compreender como calculá-lo e usá-lo é interessante para poder fazer declarações precisas e tomar decisões baseadas em dados. Neste artigo, explicaremos o que é, como é calculado e por que é importante na análise de dados.
O que é desvio médio?
O desvio médio é uma medida estatística que representa a média das diferenças entre cada valor de um conjunto de dados e a média aritmética desses dados. Em outras palavras, o desvio médio indica o quanto, em média, os dados se afastam da média.
Quando usar?
Abaixo, mostro alguns casos em que esse desvio pode ser muito útil:
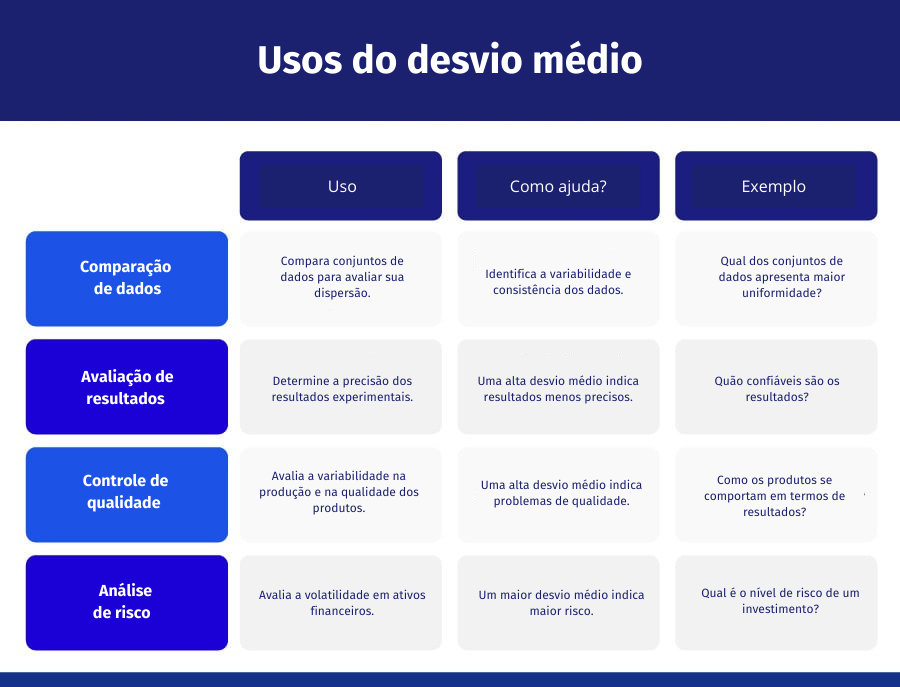
- Comparando dados: se você tiver dois conjuntos de dados com médias diferentes, ele pode ajudá-lo a determinar qual dos dois conjuntos possui mais dispersão ou variabilidade nos dados.
- Avaliando resultados: se você estiver conduzindo um experimento ou teste e tiver um conjunto de resultados, o desvio médio pode ajudá-lo a determinar a precisão dos seus resultados. Ele indica que os resultados podem ser menos precisos.
- Controle de qualidade: no controle de qualidade do produto, o desvio é frequentemente usado para avaliar a variabilidade do produto. Um desvio elevado pode indicar problemas na produção ou na qualidade do produto.
- Análise de risco: na análise de risco financeiro, ele é frequentemente utilizado para avaliar a volatilidade de um ativo financeiro. Quanto maior for o desvio, maior será o risco associado ao ativo financeiro.
Em geral, o desvio é uma medida útil para compreender a variabilidade dos dados em um conjunto e pode ser aplicado em muitas situações diferentes.
Fórmula para calcular o desvio médio
A fórmula simples para calculá-lo é a seguinte:

Em palavras simples, para calcular o desvio, você soma as diferenças absolutas entre cada valor no conjunto de dados e sua média e divide o resultado pelo número total de pontos de dados. Esta fórmula nos dá uma medida da dispersão média dos dados do conjunto em relação à sua média.
Exemplo
Aqui está um exemplo simples de como calcular o desvio médio:
Suponha que temos o seguinte conjunto de dados: 2, 4, 6, 8, 10.
Para calculá-lo, primeiro precisamos calcular a média dos dados:
X = (2 + 4 + 6 + 8 + 10) / 5 = 6
Agora podemos calcular o desvio usando a fórmula:
Desvio médio = Σ | Xi-X | /N
DM = (|2 – 6| + |4 – 6| + |6 – 6| + |8 – 6| + |10 – 6|) / 5
DM = (4 + 2 + 0 + 2 + 4) / 5
MS = 2,4
Portanto, o desvio deste conjunto de dados é 2,4. Isso significa que, em média, os valores do conjunto diferem em 2,4 unidades da sua média.
Diferença entre desvio médio e desvio padrão
Tanto o desvio médio quanto o desvio padrão são medidas de dispersão utilizadas para avaliar a variabilidade dos dados em um conjunto. No entanto, existem algumas diferenças importantes entre eles:
- Fórmula de Cálculo:
- O desvio médio é calculado tomando a média aritmética das diferenças absolutas entre cada valor e a média do conjunto. A fórmula para o desvio médio é: Desvio Meˊdio (DM)=1𝑛∑𝑖=1𝑛∣𝑥𝑖−𝑥ˉ∣Desvio Meˊdio (DM)=n1∑i=1n∣xi−xˉ∣ Onde 𝑥𝑖xi são os valores individuais dos dados, 𝑥ˉxˉ é a média aritmética e 𝑛n é o número de observações.
- O desvio padrão é calculado extraindo a raiz quadrada da variância. A fórmula para o desvio padrão 𝜎σ é: 𝜎=1𝑛∑𝑖=1𝑛(𝑥𝑖−𝑥ˉ)2σ=n1∑i=1n(xi−xˉ)2
- Sensibilidade a Valores Extremos:
- O desvio médio é mais sensível a valores extremos ou discrepantes no conjunto de dados, pois é calculado utilizando as diferenças absolutas entre cada valor e a média.
- O desvio padrão é menos sensível a valores extremos, uma vez que se baseia na média dos quadrados das diferenças, o que reduz o efeito dos valores extremos na medida.
- Interpretação:
- O desvio médio é interpretado como a medida média da distância dos valores no conjunto de dados em relação à média.
- O desvio padrão é interpretado como a medida média da distância que os valores do conjunto de dados possuem em relação à média, em termos do seu desvio padrão.
Em resumo, o desvio médio e o desvio padrão são ambas medidas de dispersão úteis, porém com propósitos e interpretações ligeiramente diferentes.
O desvio médio é mais sensível a valores extremos, enquanto o desvio padrão é menos sensível e proporciona uma interpretação mais clara em termos da dispersão dos dados em relação à média. A escolha entre essas medidas depende do contexto e dos objetivos da análise estatística.
Concluindo, eleé de fato uma medida crucial de dispersão na análise de dados, pois nos ajuda a compreender o quanto os dados variam em relação a uma média definida.
Ao calcular e analisar, podemos obter uma compreensão mais profunda dos dados, permitindo-nos tomar decisões baseadas em fatos com maior precisão.
Com o uso da ferramenta de pesquisa e análise de dados do QuestionPro, você pode coletar e analisar seus dados de pesquisa de forma eficiente.
Além disso, a ampla gama de ferramentas oferecidas pela QuestionPro permite que você aprofunde sua análise e obtenha insights valiosos a partir dos seus dados.
Não hesite em aproveitar o QuestionPro em seu próximo projeto. Solicite uma demonstração agora mesmo ou comece a usar uma conta gratuita para explorar todas as funcionalidades disponíveis.



