
O desvio padrão é uma das principais medidas estatísticas utilizadas no cálculo da amostra em pesquisas e também desempenha um papel fundamental como medida de risco para analistas, gestores de investimento e consultores.
Neste artigo, exploraremos detalhadamente o conceito, seus usos em diferentes contextos e forneceremos um guia passo a passo sobre como calculá-lo. Se você deseja compreender melhor essa importante métrica estatística e sua aplicação prática, continue lendo!
O que é desvio padrão?
O desvio padrão é uma medida de extensão ou variabilidade na estatística descritiva. É usado para calcular a variação ou dispersão dos pontos de dados individuais em relação à média.
Um desvio baixo indica que os pontos de dados estão muito próximos da média, enquanto um desvio alto indica que os dados estão dispersos em um intervalo maior de valores.
No campo do marketing, o desvio pode ajudar a considerar a grande variação nos custos ou vendas. Ele também ajuda a determinar a dispersão dos preços dos ativos em relação ao seu preço médio e a volatilidade do mercado.
Importância do desvio padrão
O desvio padrão é uma métrica importante na análise estatística. Algumas das razões para isso incluem:
Inclui todas as observações
Uma vantagem do desvio padrão é que cada dado é levado em conta na análise. Outras formas de medir a dispersão, como o intervalo, consideram apenas os pontos extremos e não avaliam os valores intermediários. Por isso, o desvio padrão é frequentemente considerado uma forma mais precisa e confiável de medir a dispersão do que outras métricas.
Pode ser usado em combinação
Usando um determinado método, os desvios padrão de dois conjuntos de dados podem ser somados. Não existem métodos semelhantes para outras medidas de dispersão em estatística. Além disso, ao contrário de outras formas de observação, o desvio padrão pode ser utilizado em outros cálculos matemáticos.
Indica quando um conjunto é distribuído de forma desigual
O desvio padrão é muito útil para determinar o quão desigualmente os dados estão distribuídos. Ele não só informa a amplitude dos dados, mas também revela a desigualdade na distribuição.
Suporta análises matemáticas e estatísticas
O valor do desvio padrão é sempre definido de forma clara, permitindo a realização de análises matemáticas e estatísticas com precisão.
Permite determinar o risco de um investimento
A quantidade de pontos de dados que se afastam da média pode ser usada para calcular o risco de um investimento. Quanto maior o desvio da média, maior o risco associado ao investimento.
Exemplo de desvio padrão em pesquisa
Imagine que você está realizando uma pesquisa de satisfação com clientes de uma empresa e coletou as respostas em uma escala de 1 a 10. Os dados coletados são os seguintes:
Respostas dos clientes (nota de 1 a 10): 7, 8, 6, 5, 9, 8, 7, 6, 9, 7
Para calcular o desvio padrão e entender a dispersão dos dados, siga os passos abaixo:
- Calcule a média (média aritmética):
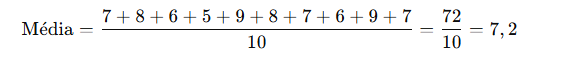
Calcule as diferenças entre cada valor e a média:
- 7−7,2=−0,27 – 7,2 = -0,27−7,2=−0,2
- 8−7,2=0,88 – 7,2 = 0,88−7,2=0,8
- 6−7,2=−1,26 – 7,2 = -1,26−7,2=−1,2
- 5−7,2=−2,25 – 7,2 = -2,25−7,2=−2,2
- 9−7,2=1,89 – 7,2 = 1,89−7,2=1,8
- 8−7,2=0,88 – 7,2 = 0,88−7,2=0,8
- 7−7,2=−0,27 – 7,2 = -0,27−7,2=−0,2
- 6−7,2=−1,26 – 7,2 = -1,26−7,2=−1,2
- 9−7,2=1,89 – 7,2 = 1,89−7,2=1,8
- 7−7,2=−0,27 – 7,2 = -0,27−7,2=−0,2
Eleve ao quadrado as diferenças:
- (−0,2)2=0,04(-0,2)^2 = 0,04(−0,2)2=0,04
- (0,8)2=0,64(0,8)^2 = 0,64(0,8)2=0,64
- (−1,2)2=1,44(-1,2)^2 = 1,44(−1,2)2=1,44
- (−2,2)2=4,84(-2,2)^2 = 4,84(−2,2)2=4,84
- (1,8)2=3,24(1,8)^2 = 3,24(1,8)2=3,24
- (0,8)2=0,64(0,8)^2 = 0,64(0,8)2=0,64
- (−0,2)2=0,04(-0,2)^2 = 0,04(−0,2)2=0,04
- (−1,2)2=1,44(-1,2)^2 = 1,44(−1,2)2=1,44
- (1,8)2=3,24(1,8)^2 = 3,24(1,8)2=3,24
- (−0,2)2=0,04(-0,2)^2 = 0,04(−0,2)2=0,04
Calcule a média das diferenças ao quadrado (variância):
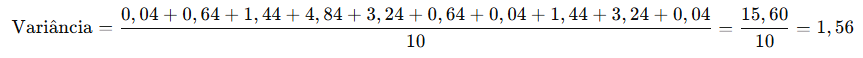
Tire a raiz quadrada da variância para encontrar o desvio padrão:
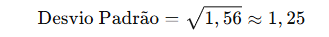
Interpretação:
O desvio padrão de 1,25 indica que, em média, as respostas dos clientes estão a cerca de 1,25 pontos da média de 7,2. Isso significa que as respostas variam moderadamente em torno da média. Quanto maior o desvio padrão, maior a dispersão dos dados em relação à média.
Fórmula do desvio padrão de uma amostra
Ele é um componente fundamental para calcular o tamanho da amostra de pesquisa. A fórmula para calculá-lo é a seguinte:

- S = Desvio padrão.
- ∑ = Soma de.
- X = Cada valor.
- x̅ = Média aritmética.
Como calcular o desvio padrão de uma amostra?
Para calcular o desvio de uma amostra de pesquisa, basta seguir estes passos:
- Calcule a média de todos os pontos de dados. A média é calculada somando todos os pontos de dados e dividindo pelo número de pontos de dados.
- Calcule a variância de cada ponto de dados subtraindo a medida da média do valor do ponto de dados.
- Eleve ao quadrado a variância de cada ponto de dados obtida no passo 2.
- Some os valores da variância ao quadrado obtidos no passo 3.
- Divida a soma dos valores da variância ao quadrado obtidos no passo 4 pelo número de pontos de dados do conjunto de dados menos 1.
- Tire a raiz quadrada do quociente do resultado obtido no passo 5.
Confira os principais usos
Alguns usos comuns do desvio padrão são:
1. Medir o risco de investimentos
Muitas empresas de investimento utilizam o cálculo para entender o quão diferente o desempenho do fundo é em relação ao retorno normalmente esperado.
Como é uma estatística fácil de entender, essa medida pode ser comunicada aos clientes finais e investidores. Dessa forma, o desvio padrão permite avaliar a volatilidade dos valores no mercado e prever tendências futuras de desempenho.
2.Compreender melhor conjuntos de dados
Ele é usado para medir a dispersão dos valores em um conjunto de dados. Indivíduos e empresas o utilizam o tempo todo em diferentes campos para entender melhor os conjuntos de dados.
3. Compreender o desempenho dos anúncios
Profissionais de marketing frequentemente calculam o desvio da receita obtida por cada anúncio para entender qual variação é esperada na receita de um anúncio específico.
Neste contexto, também é possível calcular o desvio do número de anúncios utilizados pelos concorrentes para entender se estão usando mais ou menos anúncios do que o normal durante um período determinado.
4- Utilização em Recursos Humanos
Parte do papel do gestor de recursos humanos é calcular essa medida dos salários em um campo específico para entender que tipo de variação salarial devem oferecer aos novos funcionários.
Agora que você conhece todos os aspectos básicos sobre o desvio padrão, que tal colocá-lo em prática nas suas pesquisas?
Utilize o desvio padrão nas suas análises com a QuestionPro para obter uma visão mais precisa sobre a dispersão dos seus dados. Experimente agora e aproveite todos os benefícios dessa métrica poderosa!
Perguntas frequentes
O desvio médio é uma medida estatística que indica o quão dispersos estão os valores de um conjunto de dados em relação à média. Ele é calculado pela média dos valores absolutos das diferenças entre cada ponto de dados e a média.
O desvio médio calcula a média das diferenças absolutas entre os dados e a média, enquanto o desvio padrão leva em consideração as diferenças elevadas ao quadrado, o que torna o desvio padrão mais sensível a valores extremos.
O desvio médio é útil quando você deseja uma medida simples de dispersão que não seja sensível a valores extremos. Ele é frequentemente utilizado quando se quer uma noção geral da variabilidade dos dados, sem as influências de outliers.



