A função de Gauss, também conhecida como Distribuição Normal, leva o nome do matemático alemão Carl Friedrich Gauss, e se tornou um pilar essencial na análise estatística e é usada em diversas disciplinas. Neste artigo, exploramos a função desde a sua definição até às suas aplicações práticas, destacando as suas vantagens e características. Boa leitura!
O que é função de Gauss?
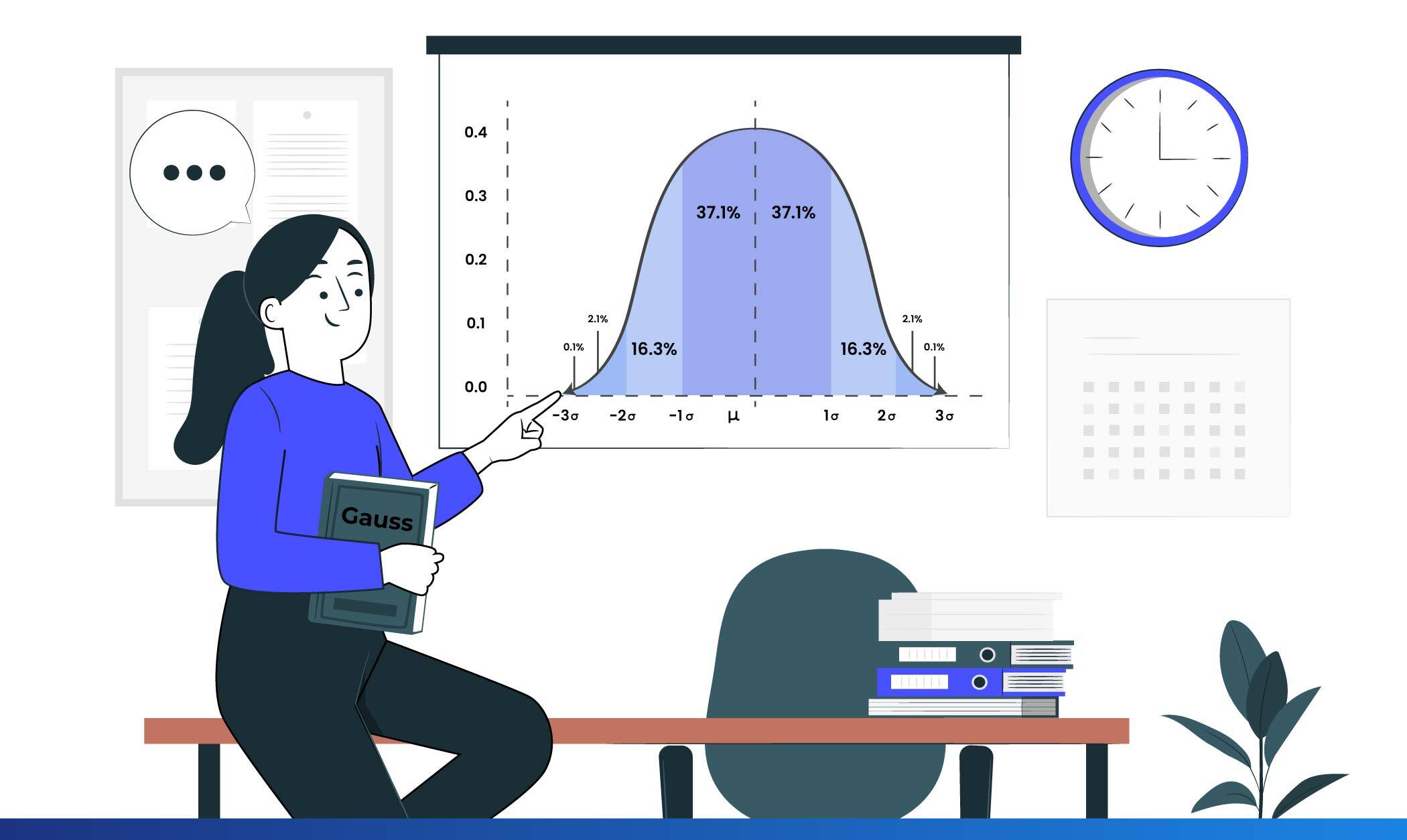
É uma função matemática que descreve a forma como os dados são distribuídos em um conjunto. Caracteriza-se pela sua forma simétrica e pela famosa aparência em forma de sino, com a maior parte dos dados concentrados em torno da média e dispersos uniformemente para ambos os lados. A função é definida por dois parâmetros principais: a média, que representa o centro da distribuição, e o desvio padrão, que mede a dispersão dos dados.
Sua forma simétrica implica que metade dos dados está à esquerda da média e a outra metade à direita. Além disso, cerca de 68% dos dados estão dentro de um desvio padrão da média, enquanto 95% estão dentro de dois desvios padrão.
Outra característica interessante é que, independentemente do formato da distribuição original, quando dados suficientes se acumulam, a distribuição tende a seguir um formato de sino gaussiano. Este fenômeno é conhecido como Teorema do Limite Central, que destaca a prevalência desta distribuição na análise estatística.
Vantagens da função de Gauss: Por que é tão poderosa?
A popularidade reside em várias vantagens importantes. Primeiro, é altamente intuitiva e fácil de entender, o que a torna uma ferramenta acessível mesmo para quem não tem uma vasta formação matemática. Além disso, sua ampla aplicabilidade permite modelar com precisão uma vasta gama de situações do mundo real.
Outra vantagem fundamental é a capacidade de resumir a informação em dois parâmetros: a média e o desvio padrão. Isso simplifica muito a análise e interpretação dos dados, permitindo que pesquisadores e analistas obtenham informações valiosas de forma eficiente.
O Teorema do Limite Central afirma que, dado um tamanho de amostra suficientemente grande, a distribuição da média das amostras aproxima-se de uma distribuição normal, independentemente da forma da distribuição original. Isso torna a função de Gauss uma ferramenta poderosa para analisar grandes conjuntos de dados.
A função de Gauss é essencial em muitos testes estatísticos, como o teste t de Student e o teste qui-quadrado. Esses testes baseiam-se em suposições de normalidade para fazer inferências sobre as populações.
Usos da função de Gauss
Ela é aplicada em uma ampla variedade de campos devido à sua versatilidade e capacidade de modelar inúmeros fenômenos. Alguns dos usos mais comuns incluem:
Estatística descritiva
A função de Gauss é essencial para descrever a distribuição de dados em uma população. É usada para resumir e compreender a tendência central e a dispersão de um conjunto de dados.
Inferência estatística
Na inferência estatística, ela é crucial para fazer previsões e estimativas. Permite calcular intervalos de confiança e realizar testes de hipóteses, fornecendo ferramentas fundamentais para a tomada de decisões baseadas em dados.
Pesquisa psicológica
Em psicologia, é usada para modelar vários fenômenos, como a distribuição de quocientes de inteligência (QI) em uma população. Além disso, é utilizada em estudos comportamentais e na análise de resultados de testes psicométricos.
Economia e finanças
No domínio econômico e financeiro, a função de Gauss em sino gaussiana é utilizada para modelar a variabilidade dos retornos dos ativos financeiros. O modelo de retorno logarítmico segue uma distribuição normal em muitos casos, o que facilita a avaliação de risco e a tomada de decisões de investimento.
Biologia e medicina
Na biologia, a distribuição normal é encontrada em fenômenos como a altura de uma população ou a distribuição de peso de uma espécie. Na medicina, é aplicada para analisar dados biométricos e avaliar a eficácia de tratamentos, entre outras utilizações.
Controle de qualidade
Também é utilizada no controle de qualidade para avaliar a consistência e a variabilidade na produção de bens e serviços. Permite estabelecer limites de tolerância e detectar possíveis desvios nos processos de fabricação.
Modelagem de fenômenos naturais
Em diversas disciplinas científicas, como física, meteorologia e geologia, ela é utilizada para modelar a distribuição de variáveis, como velocidade do vento, temperatura ou concentração de produtos químicos em uma determinada área.
Aprendizado de máquina e ciência de dados
No campo do aprendizado de máquina, a função de Gauss é usada como suposição inicial em muitos algoritmos e modelos. Além disso, é comum assumir que os erros de predição seguem uma distribuição normal, o que facilita o desenvolvimento e a interpretação dos modelos.
Exemplo de função de Gauss
Vamos imaginar que estamos analisando o desempenho acadêmico dos alunos de um ensino médio. Queremos entender como as pontuações são distribuídas em um teste de matemática e usar a função para obter informações valiosas sobre o desempenho geral da turma.
Etapa 1: Coleta de dados
Obtemos as notas de todos os alunos no teste de matemática. Suponha que coletamos as seguintes classificações em uma escala de 0 a 100:
78, 82, 85, 88, 90, 92, 94, 96, 98, 100
Etapa 2: Cálculo da média e desvio padrão
Calculamos a média e o desvio padrão desses escores. Suponha que a média seja 90 e o desvio padrão seja 6. Esses valores são apenas para ilustrar o exemplo; em um cenário real, seriam calculados a partir de dados reais.
Etapa 3: Criando a função de Gauss
Usando a média e o desvio padrão, podemos criar a função de Gauss que descreve a distribuição das pontuações. A maioria dos alunos agrupa-se em torno da média, e o formato do sino reflete a probabilidade de obter notas diferentes.
Etapa 4: Interpretação
- 68% dos Alunos: Cerca de 68% dos alunos terão pontuação dentro de um desvio padrão da média, ou seja, entre 84 e 96.
- 95% dos Alunos: Cerca de 95% dos alunos terão pontuações dentro de dois desvios padrão da média, na faixa de 78 a 102.
- 99,7% dos Alunos: Praticamente todos os alunos (99,7%) obterão pontuações dentro de três desvios padrão da média, entre 72 e 108.
Etapa 5: Tomada de decisão e avaliação de desempenho
Com esta distribuição, os educadores podem tomar decisões informadas sobre a eficácia dos testes e do ensino. Por exemplo, se um grande número de alunos obtiver pontuações abaixo da média, isso poderá indicar áreas para melhoria no ensino. Além disso, proporciona uma compreensão clara de como as notas são distribuídas, o que pode ajudar a estabelecer padrões de desempenho e políticas educacionais.
Conclusão
Em suma, a função de Gauss é mais do que apenas uma curva matemática; é uma ferramenta essencial que se mostrou útil em diversas disciplinas. Sua simplicidade, versatilidade e capacidade de resumir dados complexos em parâmetros-chave a tornam um componente fundamental da análise estatística.
À medida que continuamos a explorar e compreender o mundo que nos rodeia, a função de Gauss continuará a desempenhar um papel crucial na nossa capacidade de modelar e compreender fenômenos com precisão e clareza.
Se você está procurando ferramentas para coletar dados de qualidade para seus próximos projetos, lembre-se que na QuestionPro podemos ajudá-lo. Comece criando uma conta gratuita para nosso software de pesquisa e descubra todo o seu potencial.



