
O teste Kruskal-Wallis leva o nome de William Kruskal e W. Allen Wallis e é usado em estatística para verificar se um conjunto de dados vem ou não da mesma população. Neste artigo, você descobrirá em que consiste, quais são suas vantagens e como desenvolvê-lo passo a passo.
O que é o teste Kruskal-Wallis?
É um teste não paramétrico baseado em classificação que pode ser usado para verificar se existem diferenças estatisticamente relevantes entre dois ou mais grupos de uma variável independente em uma variável dependente ordinal ou contínua.
O teste determina se as medianas de dois ou mais grupos são diferentes. Ele calcula uma estatística de teste e a compara com um ponto de corte da distribuição.
A estatística de teste usada é chamada de estatística H. As hipóteses de teste são:
- H0: As medianas populacionais são iguais.
- H1: As medianas populacionais não são iguais.
Qual é a importância do teste Kruskal-Wallis?
Ele é considerado a alternativa não paramétrica à ANOVA unidirecional e uma extensão do teste U de Mann-Whitney, permitindo a comparação de mais de dois grupos independentes.
O teste H é utilizado quando os pressupostos da ANOVA (como o pressuposto de normalidade) não são atendidos. Às vezes, ele é chamado de ANOVA unidirecional em intervalos porque o teste usa os intervalos dos valores dos dados em vez dos pontos de dados reais.
Por ser não paramétrico, o teste não pressupõe que os dados provêm de uma distribuição específica. O teste Kruskal-Wallis indicará se há uma diferença significativa entre os grupos. No entanto, ele não especifica quais grupos são diferentes.
Vantagens de usar modelos Kruskal-Wallis
Algumas das vantagens são:
- Pode ser aplicado a um grande número de situações.
- É facilmente compreendido intuitivamente.
- Pode ser usado com tamanhos de amostra menores.
- Pode ser usado com vários tipos de dados.
- Requer menos suposições ou suposições menos rigorosas sobre a natureza da distribuição da população.
- Geralmente é robusto e não é afetado por valores extremos nos dados, como valores discrepantes.
- Possui um alto nível de eficiência assintótica relativa em comparação com testes paramétricos clássicos.
Quando o teste Kruskal-Wallis pode ser usado?
Quando você decide analisar seus dados usando um teste H de Kruskal-Wallis, parte do processo é verificar se os dados podem realmente ser analisados usando esse teste.
Só é apropriado usar um teste H de Kruskal-Wallis se seus dados “passarem” em quatro suposições necessárias para que o teste produza um resultado válido:
- Premissa nº 1: É necessário medir sua variável dependente em nível ordinal ou contínuo.
- Premissa nº 2: Dois ou mais grupos categóricos e independentes constituem sua variável independente.
- Premissa nº 3: O teste H de Kruskal-Wallis é usado principalmente quando você tem três ou mais grupos categóricos independentes, mas pode ser usado para apenas dois grupos.
- Premissa nº 4: É necessário que haja independência das observações, ou seja, não deve haver relação entre as observações dos grupos ou entre os grupos.
Como realizar o teste Kruskal-Wallis?
Agora que você sabe em que consiste o teste de Kruskal-Wallis, qual a sua importância e como determinar se ele pode ser utilizado, é hora de mostrar como realizá-lo passo a passo:
Etapa 1: Classifique os dados de todos os grupos ou amostras em ordem crescente em um conjunto combinado.
Etapa 2: Atribua intervalos aos pontos de dados classificados. Atribua valores vinculados à faixa intermediária.
Passo 3: Some os diferentes intervalos de cada grupo/amostra.
Etapa 4: Calcule a estatística H
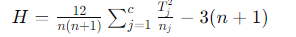
Onde:
- nnn = soma dos tamanhos amostrais para todas as amostras.
- ccc = número de amostras.
- TjT_jTj = soma dos postos da amostra.
- njn_jnj = tamanho da amostra.
Etapa 5: Encontre o valor crítico do qui-quadrado, com c−1c-1c−1 graus de liberdade. Para c=3c = 3c=3 grupos, há 3−1=23 – 1 = 23−1=2 graus de liberdade. Para um nível alfa de 0,05, o valor crítico do qui-quadrado é 5,9915.
Etapa 6: Compare o valor H da Etapa 4 com o valor crítico do qui-quadrado da Etapa 5.
- Se o valor crítico do qui-quadrado for menor que a estatística H, rejeite a hipótese nula de que as medianas são iguais.
- Se o valor do qui-quadrado não for inferior à estatística H, não há evidências suficientes para sugerir que as medianas sejam desiguais.
Conclusão
Como qualquer teste não paramétrico, a utilização do teste de Kruskal-Wallis é conveniente quando se trabalha com amostras pequenas, corroborando os resultados obtidos com base na teoria normal.
Se você deseja explorar mais ferramentas de pesquisa, convidamos você a baixar nosso Ebook de Metodologias Avançadas de Pesquisa, onde encontrará informações detalhadas sobre técnicas como análise conjunta, lógica de pesquisa avançada, relatórios e métodos de análise para garantir o sucesso em sua próxima investigação.
Lembre-se também que o QuestionPro Audience oferece diversos serviços de pesquisa e coleta de amostras de respondentes, além de nossa plataforma de pesquisas online gratuita. Para mais informações, entre em contato conosco através do nosso chat online e compartilhe suas necessidades.



