
A variância é a medida de dispersão mais amplamente utilizada, junto com o desvio padrão. É uma medida confiável ao analisar dados de uma distribuição. Ao compará-lo com a média, você pode reconhecer a presença de valores discrepantes ou dados distantes. Vamos conhecer mais sobre essa medida, suas características, vantagens e como calculá-la.
O que é variação?
É uma medida de dispersão que representa a variabilidade de uma série de dados em relação à sua média. Formalmente, é calculado como a soma dos quadrados dos resíduos dividida pelo total de observações.
Também pode ser calculado como o desvio padrão ao quadrado. Aliás, entendemos resíduo como a diferença entre o valor de uma variável por vez e o valor médio de toda a variável.
Quando usar variância?
Aqui estão algumas situações em que você pode usar a variância:
- Análise de dispersão: Quando você precisa entender o quanto os dados estão dispersos em relação à média. Se a variância for baixa, significa que os dados estão próximos da média; se for alta, os dados estão mais espalhados.
- Comparação entre conjuntos de dados: Ao comparar diferentes conjuntos de dados, a variância pode ajudá-lo a ver qual conjunto tem maior dispersão. Por exemplo, se você está comparando o desempenho de duas equipes, a variância pode mostrar qual equipe apresenta mais variação no desempenho.
- Controle de qualidade: Em processos industriais ou comerciais, a variância é usada para monitorar a consistência e a qualidade de um produto. Quanto menor a variância, mais consistente é o processo de produção.
- Cálculo do risco em investimentos financeiros: Em finanças, a variância (ou o desvio padrão, que é a raiz quadrada da variância) é usada para medir o risco ou a volatilidade de um ativo. Uma variância alta indica que o preço do ativo é mais volátil e arriscado.
- Análises de ANOVA (Análise de Variância): Quando você está realizando um teste de ANOVA para comparar as médias de mais de dois grupos. A variância entre os grupos ajuda a identificar se as diferenças observadas nas médias são estatisticamente significativas.
- Previsão e modelagem estatística: Em modelos preditivos, a variância pode ajudar a entender como os erros ou os resíduos do modelo se distribuem, permitindo melhorar a precisão das previsões.
- Estudos de variabilidade em experimentos: Em experimentos científicos ou de pesquisa, a variância é usada para avaliar a variabilidade dos resultados e garantir que as conclusões sejam robustas, independentemente de pequenas variações nos dados.
Tipos de Variância
A variância é uma medida estatística que indica o grau de dispersão de um conjunto de dados em relação à média. Existem alguns tipos de variância que podem ser calculados dependendo do contexto ou do conjunto de dados:
Variância Populacional
É a variância calculada com base em todos os elementos de uma população. A fórmula é:
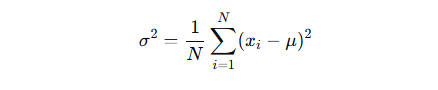
Onde:
- σ2\sigma^2σ2 é a variância populacional,
- NNN é o número total de elementos na população,
- xix_ixi são os valores dos dados,
- μ\muμ é a média da população.
Variância Amostral
Quando se trabalha com uma amostra (um subconjunto da população), a variância amostral é usada para estimar a variância populacional. A fórmula é:
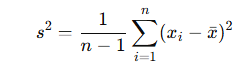
Onde:
- s2s^2s2 é a variância amostral,
- nnn é o número de elementos na amostra,
- xix_ixi são os valores dos dados,
- xˉ\bar{x}xˉ é a média da amostra.
- Variância de Entre Grupos (Variância Explicada): Em análises de variância (ANOVA), a variância entre os grupos reflete as diferenças entre as médias dos diferentes grupos.
- Variância de Dentro de Grupos (Variância Inexplicada): Também em ANOVA, a variância dentro de grupos representa as variações dos dados individuais dentro de cada grupo.
Vantagens e desvantagens da variação
A variância é usada para ver como os números individuais dentro de um conjunto de dados estão relacionados, em vez de usar técnicas matemáticas mais amplas.
Também se distingue por tratar todos os desvios da média como se fossem iguais, independentemente da sua direção. Os desvios quadrados não podem somar zero e dão a impressão de que não há variabilidade nos dados.
No entanto, uma desvantagem é que dá mais peso aos valores discrepantes. São números longe da média. A quadratura desses números pode distorcer os dados.
Outra desvantagem do uso da variância é que ela não é fácil de interpretar. Geralmente é usado principalmente para tirar a raiz quadrada de seu valor, o que indica o desvio padrão dos dados.
Exemplo de variação
Aqui está um exemplo hipotético para demonstrar como funciona a variância, é o caso da área financeira. Suponha que os retornos das ações da Empresa ABC sejam de 10% no primeiro ano, 20% no segundo e -15% no terceiro. A média desses três retornos é de 5%. As diferenças entre cada desempenho e a média são de 5%, 15% e -20% para cada ano consecutivo.
A quadratura desses desvios dá 0,25%, 2,25% e 4,00%, respectivamente. Se somarmos esses desvios quadrados, obtemos um total de 6,5%. Se dividirmos a soma de 6,5% por um menos o número de retornos no conjunto de dados, por se tratar de uma amostra (2 = 3-1), teremos uma variância de 3,25% (0,0325). Tirar a raiz quadrada da variância dá um desvio padrão de 18% (√0,0325 = 0,180) para os retornos.
Como a variação é calculada?
Siga estas etapas para calcular a variação:
- Calcule a média dos dados.
- Encontre a diferença de cada ponto de dados em relação ao valor médio.
- Eleve ao quadrado cada um desses valores.
- Adicione todos os valores quadrados.
- Divida esta soma dos quadrados por n – 1 (para uma amostra) ou N (para a população).
Fórmula para calcular a variância

Antes de examinar a fórmula, deve-se dizer que a variação nas estatísticas é muito importante. Porque, embora seja uma medida simples, pode fornecer muitas informações sobre uma variável específica.
A unidade de medida será sempre a unidade de medida correspondente aos dados mas ao quadrado. A variância é sempre maior ou igual a zero. Como os resíduos são elevados ao quadrado, é matematicamente impossível que a variância seja negativa. E, portanto, não pode ser menor que zero.
Qual é a diferença entre variância e desvio padrão?
Na realidade, ambos estão medindo a mesma coisa. A variância é o desvio padrão ao quadrado. Ou, inversamente, o desvio padrão é a raiz quadrada da variância.
O desvio padrão é operado nas unidades de medida originais. É claro que, como isso é normal, pode-se perguntar qual é o significado da variância como conceito. Pois bem, embora a interpretação do valor que ele retorna não nos dê muitas informações, seu cálculo é necessário para obter o valor dos demais parâmetros.
Para calcular a covariância precisamos da variância e não do desvio padrão, para calcular algumas matrizes econométricas utiliza-se a variância e não o desvio padrão. É uma questão de conforto trabalhar com os dados de acordo com quais cálculos.
Por que o desvio padrão é frequentemente usado mais do que a variância?
O desvio padrão é a raiz quadrada da variância. Às vezes é mais útil, pois tirar a raiz quadrada elimina as unidades da análise. Isso permite que comparações diretas sejam feitas entre coisas diferentes que podem ter unidades ou magnitudes diferentes.
Por exemplo, dizer que aumentar X em uma unidade aumenta Y em dois desvios padrão nos permite compreender a relação entre X e Y independentemente das unidades em que são expressos.
Conclusão
A variância é usada em estatística e probabilidade como medida para caracterizar a dispersão de uma distribuição ou amostra. Especificamente, é definido como a média dos quadrados dos desvios da média. Considerar o quadrado desses desvios evita que os desvios positivos e negativos se anulem.
Visualmente, uma distribuição com uma grande variância será mais espalhada, enquanto uma distribuição com uma pequena será muito estreita em torno da sua média.
Lembre-se que também temos outras ferramentas como a calculadora de amostras e claro, a nossa plataforma de pesquisa online. Crie já a sua conta!



