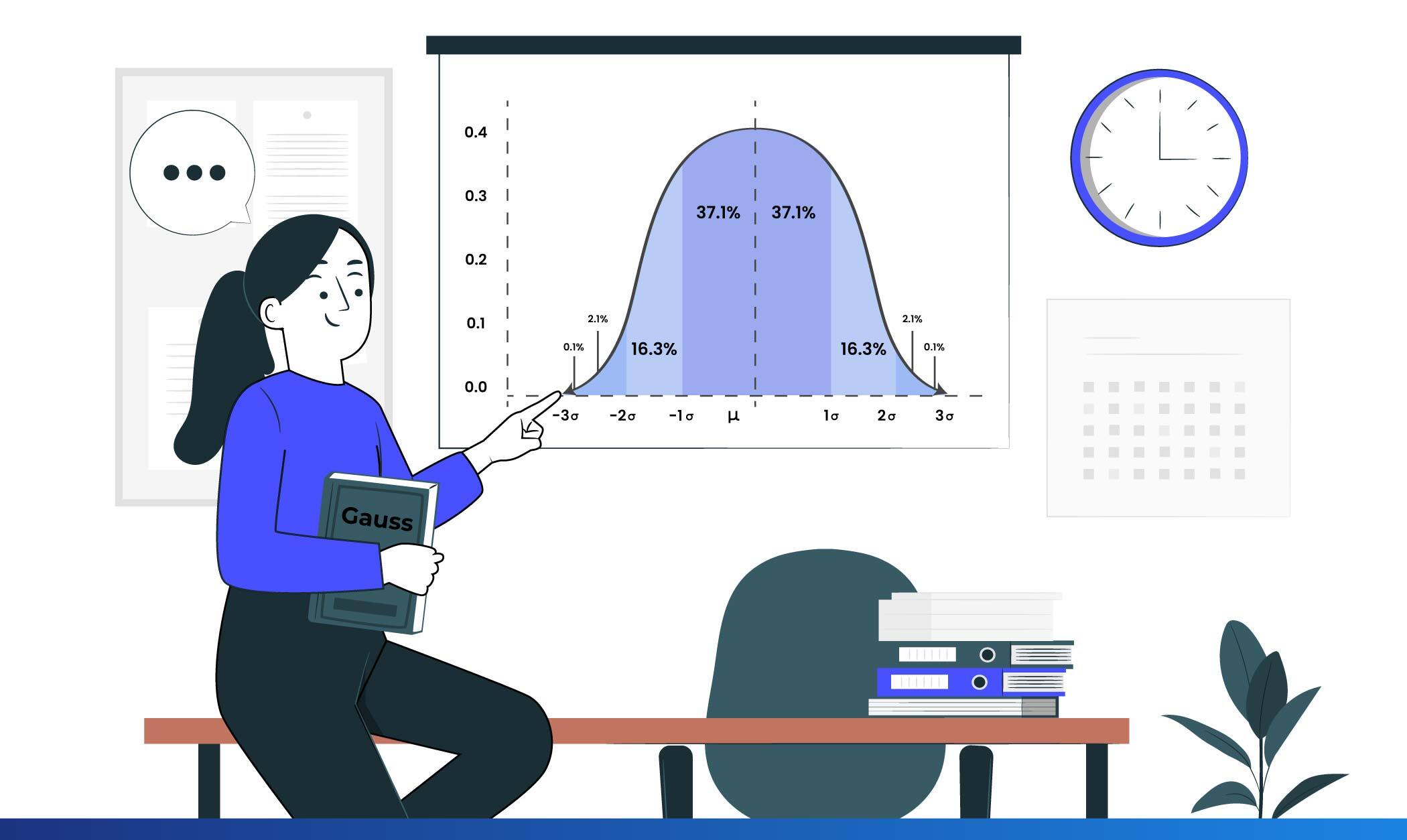
O sino gaussiano, também conhecido como Distribuição Normal, tem o nome do matemático alemão Carl Friedrich Gauss e tornou-se um pilar essencial na análise estatística, sendo utilizado numa variedade de disciplinas.
Neste artigo, exploramos o sino gaussiano desde a sua definição até às suas aplicações práticas, destacando as suas vantagens e caraterísticas distintivas.
O que é um sino gaussiano?
O sino gaussiano, ou distribuição normal, é uma função matemática que descreve a forma como os dados se distribuem num conjunto. Caracteriza-se pela sua forma simétrica e pelo famoso aspeto em forma de sino, com a maioria dos dados concentrados em torno da média e dispersos uniformemente para ambos os lados. A função é definida por dois parâmetros principais: a média, que representa o centro da distribuição, e o desvio-padrão, que mede a dispersão dos dados.
A sua forma simétrica significa que metade dos dados se situa à esquerda da média e a outra metade à direita. Além disso, cerca de 68% dos dados estão dentro de um desvio padrão da média, enquanto 95% estão dentro de dois desvios padrão.
Outra caraterística interessante é que, independentemente da forma da distribuição original, quando se acumulam dados suficientes, a distribuição tende a seguir uma forma de sino gaussiana. Este fenómeno é conhecido como o Teorema do Limite Central, que sublinha a importância desta distribuição na análise estatística.
Vantagens do sino gaussiano: Porque é que é tão poderoso?
A popularidade do sino gaussiano reside em várias vantagens fundamentais. Em primeiro lugar, é altamente intuitivo e fácil de compreender, o que o torna uma ferramenta acessível mesmo para quem não tem uma formação matemática extensa. Além disso, a sua ampla aplicabilidade permite-lhe modelar com precisão uma vasta gama de situações do mundo real.
Outra vantagem importante é a sua capacidade de resumir a informação em dois parâmetros: a média e o desvio padrão. Isto simplifica muito a análise e interpretação dos dados, permitindo aos investigadores e analistas obter informações valiosas de forma eficiente.
O Teorema do Limite Central afirma que, dado um tamanho de amostra suficientemente grande, a distribuição das médias da amostra se aproxima de uma distribuição normal, independentemente da forma da distribuição original. Isto faz com que o sino gaussiano seja uma ferramenta poderosa para a análise de grandes conjuntos de dados.
O sino gaussiano é fundamental para muitos testes estatísticos, como o teste t de Student e o teste do qui-quadrado. Estes testes baseiam-se em pressupostos de normalidade para fazer inferências sobre populações.
Utilizações do sino gaussiano
O sino gaussiano é aplicado numa grande variedade de domínios, desde a física e a biologia à economia e à psicologia. Em estatística, é normalmente utilizada para modelar fenómenos naturais, como a altura de uma população ou resultados de testes. Além disso, esta distribuição é utilizada como base para outras ferramentas estatísticas e modelos mais complexos.
O sino gaussiano, ou distribuição normal, é utilizado numa grande variedade de campos devido à sua versatilidade e capacidade de modelar numerosos fenómenos. Algumas das utilizações mais comuns incluem:
Estatísticas descritivas:
O sino gaussiano é fundamental para descrever a distribuição de dados numa população. É utilizado para resumir e compreender a tendência central e a dispersão de um conjunto de dados.
Inferência estatística:
Na inferência estatística, o sino gaussiano é crucial para fazer previsões e estimativas. Permite o cálculo de intervalos de confiança e a realização de testes de hipóteses, fornecendo ferramentas fundamentais para a tomada de decisões baseadas em dados.
Investigação psicológica:
Em psicologia, o sino gaussiano é utilizado para modelar vários fenómenos, como a distribuição dos quocientes de inteligência (QI) numa população. É também utilizado em estudos comportamentais e na análise de resultados de testes psicométricos.
Economia e finanças:
Em economia e finanças, o sino gaussiano é utilizado para modelar a variabilidade das rendibilidades dos activos financeiros. O modelo de retornos logarítmicos segue uma distribuição normal em muitos casos, o que facilita a avaliação do risco e a tomada de decisões de investimento.
Biologia e medicina:
Em biologia, a distribuição normal é encontrada em fenómenos como a altura de uma população ou a distribuição do peso numa espécie. Em medicina, é aplicada para analisar dados biométricos e avaliar a eficácia dos tratamentos, entre outras utilizações.
Controlo de qualidade:
O sino gaussiano é utilizado no controlo de qualidade para avaliar a consistência e a variabilidade na produção de bens e serviços. Permite estabelecer limites de tolerância e detetar possíveis desvios nos processos de fabrico.
Modelação dos fenómenos naturais:
Em várias disciplinas científicas, como a física, a meteorologia e a geologia, o sino gaussiano é utilizado para modelar a distribuição de variáveis como a velocidade do vento, a temperatura ou a concentração de substâncias químicas numa determinada área.
Aprendizagem automática e ciência dos dados:
No domínio da aprendizagem automática, o sino gaussiano é utilizado como pressuposto inicial em muitos algoritmos e modelos. Além disso, é comum assumir que os erros de previsão seguem uma distribuição normal, o que facilita o desenvolvimento e a interpretação do modelo.
Exemplo de um sino gaussiano: Avaliação do desempenho académico
Imaginemos que estamos a analisar o desempenho académico dos alunos de uma escola secundária. Queremos compreender como se distribuem as notas num exame de matemática e utilizamos o sino gaussiano para obter informações valiosas sobre o desempenho global da turma.
Etapa 1: Recolha de dados
Obtemos as notas de todos os alunos no teste de matemática. Supõe que recolhemos as seguintes classificações numa escala de 0 a 100:
78, 82, 85, 88, 90, 92, 94, 96, 98, 100
Passo 2: Cálculo da média e do desvio-padrão
Calcula a média e o desvio padrão destas pontuações. Supõe que a média é 90 e o desvio padrão é 6. Estes valores servem apenas para ilustrar o exemplo; num cenário real, seriam calculados a partir dos dados reais.
Passo 3: Criar o sino gaussiano
Com a média e o desvio padrão, podemos criar o sino gaussiano que descreve a distribuição das notas. A maioria dos alunos concentra-se em torno da média e a forma de sino reflecte a probabilidade de obter notas diferentes.
Passo 4: Interpretação do sino gaussiano
- 68% dos alunos: Cerca de 68% dos alunos obterão notas dentro de um desvio padrão da média, ou seja, entre 84 e 96.
- 95% dos alunos: Cerca de 95% dos alunos terão notas dentro de dois desvios-padrão da média, no intervalo de 78 a 102.
- 99,7% dos alunos: Praticamente todos os alunos (99,7%) terão uma pontuação dentro de três desvios-padrão da média, entre 72 e 108.
Etapa 5: Tomada de decisões e avaliação do desempenho
Com esta distribuição, os educadores podem tomar decisões informadas sobre a eficácia dos testes e do ensino. Por exemplo, se um grande número de alunos tiver notas abaixo da média, isso pode indicar áreas que precisam de ser melhoradas no ensino. Além disso, o sino gaussiano permite compreender claramente como as notas são distribuídas, o que pode ajudar a definir padrões de desempenho e políticas educativas.
Neste caso de utilização, o sino gaussiano não só fornece um resumo visual da distribuição das notas, como também oferece ferramentas valiosas para tomar decisões educativas com base em dados estatísticos. Este exemplo ilustra como a distribuição normal pode ser uma ferramenta poderosa na avaliação e melhoria contínua do desempenho académico.
Conclusão
Em conclusão, o sino gaussiano é mais do que uma simples curva matemática; é uma ferramenta essencial que provou a sua utilidade numa variedade de disciplinas. A sua simplicidade, versatilidade e capacidade de resumir dados complexos em parâmetros-chave fazem dele um componente fundamental da análise estatística. À medida que continuamos a explorar e a compreender o mundo que nos rodeia, o sino gaussiano continuará a desempenhar um papel crucial na nossa capacidade de modelar e compreender fenómenos com precisão e clareza.
Se estás à procura de ferramentas para recolher dados de qualidade para os teus próximos projectos, lembra-te que o QuestionPro pode ajudar. Começa por criar uma conta gratuita para o nosso software de inquéritos e descobre todo o seu potencial.



