
สหสัมพันธ์เป็นแนวคิดพื้นฐานในสถิติและการวิเคราะห์ข้อมูล ซึ่งช่วยให้เข้าใจความสัมพันธ์ระหว่างตัวแปรสองตัว แม้ว่ามักจะเน้นความสัมพันธ์เชิงบวกหรือเชิงลบที่แข็งแกร่ง แต่ความสัมพันธ์เป็นศูนย์ก็มีความสําคัญไม่แพ้กัน
หมายความว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปร กล่าวอีกนัยหนึ่งการเปลี่ยนแปลงในตัวแปรหนึ่งไม่ได้ทํานายการเปลี่ยนแปลงในอีกตัวแปรหนึ่ง
ในบล็อกนี้ เราจะสํารวจแนวคิดของความสัมพันธ์เป็นศูนย์ โดยให้คําจํากัดความที่ชัดเจน ตัวอย่างตัวอย่าง และวิธีการกําหนด
ความสัมพันธ์เป็นศูนย์คืออะไร?
ความสัมพันธ์เป็นศูนย์เป็นคําศัพท์ทางสถิติที่อธิบายสถานการณ์ที่ไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว เมื่อตัวแปรสองตัวมีความสัมพันธ์เป็นศูนย์การเปลี่ยนแปลงในตัวแปรหนึ่งจะไม่คาดการณ์การเปลี่ยนแปลงในอีกตัวแปรหนึ่ง ค่าสัมประสิทธิ์สหสัมพันธ์ซึ่งวัดระดับและทิศทางของความสัมพันธ์ระหว่างตัวแปรเป็นศูนย์ในกรณีนี้
การทําความเข้าใจความสัมพันธ์นี้มีความสําคัญในการวิเคราะห์ทางสถิติ เนื่องจากช่วยระบุตัวแปรที่ไม่มีความสัมพันธ์เชิงคาดการณ์ซึ่งกันและกัน ซึ่งเป็นสิ่งสําคัญในการสร้างแบบจําลองทางสถิติหรือตีความรูปแบบข้อมูล
เหตุใด Zero Correlation จึงมีความสําคัญ
ความสัมพันธ์เป็นศูนย์เป็นแนวคิดที่สําคัญในสถิติและการวิเคราะห์ข้อมูลด้วยเหตุผลหลายประการ เช่น:
มันระบุความเป็นอิสระ
ช่วยระบุตัวแปรที่ไม่ขึ้นกับกันเป็นเส้นตรง หากตัวแปรสองตัวมีความสัมพันธ์เป็นศูนย์การเปลี่ยนแปลงในตัวแปรหนึ่งจะไม่ให้ข้อมูลใด ๆ เกี่ยวกับการเปลี่ยนแปลงในอีกตัวแปรหนึ่ง นี่เป็นสิ่งสําคัญสําหรับการทําความเข้าใจโครงสร้างของข้อมูลและความสัมพันธ์ (หรือการขาด) ระหว่างตัวแปร
ปรับปรุงแบบจําลองทางสถิติ
ในการวิเคราะห์การถดถอยและแบบจําลองทางสถิติอื่น ๆ รวมถึงตัวแปรที่มีความสัมพันธ์นี้กับตัวแปรตามสามารถเพิ่มสัญญาณรบกวนและลดพลังการคาดการณ์ของแบบจําลอง ด้วยการระบุและไม่รวมตัวแปรดังกล่าวโมเดลสามารถทําให้ง่ายขึ้นและมีประสิทธิภาพมากขึ้นซึ่งนําไปสู่ประสิทธิภาพและการตีความที่ดีขึ้น
ความสัมพันธ์นี้ช่วยหลีกเลี่ยงการตีความผิด
การทําความเข้าใจความสัมพันธ์นี้ช่วยป้องกันการตีความข้อมูลผิด
- ตัวอย่างเช่น นักวิจัยอาจอนุมานความสัมพันธ์ระหว่างตัวแปรสองตัวโดยเข้าใจผิดตามสัญชาตญาณหรือการสังเกตเบื้องต้น
การคํานวณค่าสัมประสิทธิ์สหสัมพันธ์และพบว่าเป็นศูนย์จะชี้แจงว่าไม่มีความสัมพันธ์เชิงเส้นอยู่หลีกเลี่ยงการสรุปที่ผิดพลาด
เน้นความสัมพันธ์แบบไม่เชิงเส้น
เน้นย้ําถึงความเป็นไปได้ของความสัมพันธ์แบบไม่เชิงเส้น หากตัวแปรสองตัวมีความสัมพันธ์เป็นศูนย์ ก็ไม่ได้หมายความว่าไม่เกี่ยวข้องกันเสมอไป พวกเขาอาจมีความสัมพันธ์ที่ซับซ้อนและไม่เป็นเชิงเส้น การตระหนักถึงสิ่งนี้สามารถกระตุ้นให้มีการตรวจสอบเพิ่มเติมโดยใช้วิธีการอื่น เช่น การถดถอยแบบไม่เชิงเส้นหรือการแปลงข้อมูล
ความสัมพันธ์ช่วยในการเป็นแนวทางในการออกแบบการทดลอง
ในการออกแบบการทดลองการรู้ว่าตัวแปรใดมีความสัมพันธ์เป็นศูนย์สามารถเป็นแนวทางในการเลือกตัวแปรที่จะรวมหรือควบคุมได้ สิ่งนี้ช่วยในการออกแบบการทดลองที่มีประสิทธิภาพมากขึ้นซึ่งอิทธิพลของตัวแปรที่ไม่เกี่ยวข้องจะลดลงซึ่งนําไปสู่ผลลัพธ์ที่ชัดเจนและน่าเชื่อถือยิ่งขึ้น
เข้าใจพฤติกรรมที่แปรผัน
โดยให้ข้อมูลเชิงลึกเกี่ยวกับพฤติกรรมของตัวแปรในชุดข้อมูล ในการวิเคราะห์ทางการเงิน การทําความเข้าใจว่าสินทรัพย์ใดไม่มีความสัมพันธ์กันสามารถช่วยในการกระจายพอร์ตการลงทุน เนื่องจากการรวมสินทรัพย์ดังกล่าวสามารถลดความเสี่ยงโดยรวมได้
รองรับการทดสอบสมมติฐาน
ในการทดสอบสมมติฐาน ความสัมพันธ์นี้มักเป็นสมมติฐานที่เป็นโมฆะ
- ตัวอย่างเช่นในการทดสอบว่าตัวแปรสองตัวมีความเกี่ยวข้องกันหรือไม่สมมติฐานที่เป็นโมฆะอาจระบุว่าความสัมพันธ์ระหว่างตัวแปรเหล่านี้เป็นศูนย์
การระบุว่าสิ่งนี้จริงหรือเท็จจะช่วยในการตรวจสอบหรือหักล้างสมมติฐาน
ตัวอย่างของความสัมพันธ์เป็นศูนย์คืออะไร?
ตัวอย่างของความสัมพันธ์นี้ ซึ่งการเปลี่ยนแปลงในตัวแปรหนึ่งไม่สอดคล้องกับการเปลี่ยนแปลงในตัวแปรอื่น สามารถพบได้ในฟิลด์ต่างๆ เช่น:
สาขาการวิจัย
ตัวอย่าง: จํานวนสิ่งพิมพ์ทางวิทยาศาสตร์และรสชาติไอศกรีมที่ชื่นชอบ
การศึกษาตรวจสอบความสัมพันธ์ระหว่างจํานวนสิ่งพิมพ์ทางวิทยาศาสตร์ที่นักวิจัยมีกับรสชาติไอศกรีมที่พวกเขาชื่นชอบ
ไม่มีความเชื่อมโยงเชิงตรรกะระหว่างจํานวนเอกสารทางวิทยาศาสตร์ที่นักวิจัยตีพิมพ์และความชอบสําหรับรสชาติไอศกรีมเฉพาะ ด้วยเหตุนี้ ตัวแปรทั้งสองนี้จึงคาดว่าจะแสดงความสัมพันธ์นี้
สาขาวิชา
ตัวอย่าง: ขนาดรองเท้าของนักเรียนและเกรดในวิชาคณิตศาสตร์
การศึกษาตรวจสอบว่ามีความสัมพันธ์ระหว่างขนาดรองเท้าของนักเรียนกับเกรดในวิชาคณิตศาสตร์หรือไม่
ขนาดรองเท้าเป็นลักษณะทางกายภาพที่ไม่มีผลต่อผลการเรียนของนักเรียนในวิชาคณิตศาสตร์ ดังนั้นความสัมพันธ์ระหว่างขนาดรองเท้ากับเกรดคณิตศาสตร์จึงมีแนวโน้มที่จะเป็นศูนย์
สาขาการดูแลสุขภาพ
ตัวอย่าง: กรุ๊ปเลือดและอุบัติการณ์ของไข้หวัด
การศึกษาด้านการดูแลสุขภาพตรวจสอบว่ามีความสัมพันธ์ระหว่างกรุ๊ปเลือดของบุคคลกับจํานวนครั้งที่พวกเขาเป็นไข้หวัดในหนึ่งปีหรือไม่
กรุ๊ปเลือดไม่เกี่ยวข้องกับความถี่ในการติดโรคไข้หวัด ซึ่งได้รับอิทธิพลจากปัจจัยอื่นๆ เช่น การสัมผัสกับไวรัสและความแข็งแกร่งของระบบภูมิคุ้มกัน ดังนั้นความสัมพันธ์ระหว่างกรุ๊ปเลือดกับอุบัติการณ์ของโรคไข้หวัดจึงคาดว่าจะเป็นศูนย์
จะระบุความสัมพันธ์เป็นศูนย์ได้อย่างไร?
ในที่นี้ เราจะสํารวจวิธีระบุความสัมพันธ์นี้ผ่านการตรวจสอบด้วยสายตา การคํานวณทางสถิติ การทดสอบสมมติฐาน และการวิเคราะห์ตามบริบท
1. การตรวจสอบด้วยสายตาโดยใช้ Scatter Plots
แผนภาพกระจายเป็นเครื่องมือที่มีประสิทธิภาพสําหรับการประเมินความสัมพันธ์ระหว่างตัวแปรสองตัวด้วยสายตา
สร้างพล็อตกระจาย:
- วางตัวแปรหนึ่งตัวบนแกน x และอีกตัวแปรหนึ่งบนแกน y
- มองหาแนวโน้มหรือรูปแบบที่มองเห็นได้ในจุดข้อมูล
การระบุความสัมพันธ์:
- หากจุดกระจัดกระจายแบบสุ่มโดยไม่มีแนวโน้มที่ชัดเจน (ไม่ขึ้นหรือลง) แสดงว่ามีความสัมพันธ์กัน
- การกระจายแบบสุ่มหมายความว่าไม่มีเส้น (ไม่ว่าจะเป็นเส้นตรงหรือโค้ง) ที่สามารถพอดีกับจุดข้อมูลได้ดี
ตัวอย่าง:
- ขนาดรองเท้าของนักเรียนเทียบกับเกรดคณิตศาสตร์: หากคุณพล็อตขนาดรองเท้าเทียบกับเกรดคณิตศาสตร์และเห็นจุดกระจายแบบสุ่มโดยไม่มีแนวโน้ม
2. คํานวณค่าสัมประสิทธิ์สหสัมพันธ์
ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สัน (r) เป็นการวัดสหสัมพันธ์เชิงเส้นที่พบบ่อยที่สุด
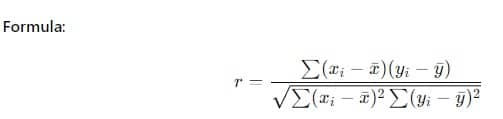
กระได:
- รวบรวมจุดข้อมูลที่จับคู่สําหรับตัวแปรทั้งสอง
- หาค่าเฉลี่ย (ค่าเฉลี่ย) ของแต่ละตัวแปร
- คํานวณระยะห่างของจุดข้อมูลแต่ละจุดจากค่าเฉลี่ย
- คูณค่าเบี่ยงเบนสําหรับแต่ละคู่และรวมผลิตภัณฑ์
- ใช้สูตรเพื่อหาค่าสัมประสิทธิ์สหสัมพันธ์
การตีความความสัมพันธ์:
ค่าใกล้เคียงกับ 0: ถ้า r r อยู่ใกล้กับ 0 แสดงว่ามีความสัมพันธ์เชิงเส้นระหว่างตัวแปรเพียงเล็กน้อยหรือไม่มีเลย
ตัวอย่าง:
- ขนาดรองเท้าและเกรดคณิตศาสตร์: หาก r ที่คํานวณได้อยู่ที่ประมาณ 0 แสดงว่ายืนยันความสัมพันธ์เป็นศูนย์
3. ทําการทดสอบสมมติฐาน
การทดสอบสมมติฐานทางสถิติสามารถระบุได้ว่าค่าสัมประสิทธิ์สหสัมพันธ์ที่สังเกตได้แตกต่างจากศูนย์อย่างมีนัยสําคัญหรือไม่
กระได:
- สมมติฐานว่าง: สมมติว่าค่าสัมประสิทธิ์สหสัมพันธ์เป็นศูนย์
- สมมติฐานทางเลือก: สมมติว่าค่าสัมประสิทธิ์สหสัมพันธ์ไม่ใช่ศูนย์
- คํานวณสถิติการทดสอบ: ใช้การทดสอบ t สําหรับค่าสัมประสิทธิ์สหสัมพันธ์
- กําหนดค่า p: เปรียบเทียบค่า p กับระดับนัยสําคัญ (เช่น 0.05)
ความสัมพันธ์เป็นศูนย์:
- หากค่า p มากกว่าระดับนัยสําคัญ อย่าปฏิเสธสมมติฐานที่เป็นโมฆะ ซึ่งบ่งชี้ว่าความสัมพันธ์ไม่แตกต่างจากศูนย์อย่างมีนัยสําคัญ
ตัวอย่าง:
- กรุ๊ปเลือดและอุบัติการณ์ของโรคไข้หวัด: การทดสอบความสัมพันธ์ระหว่างกรุ๊ปเลือดกับอุบัติการณ์ของไข้หวัดหากค่า p สูงแสดงว่าความสัมพันธ์ที่สังเกตได้ไม่มีนัยสําคัญทางสถิติซึ่งสนับสนุนความสัมพันธ์เป็นศูนย์
4. ทําความเข้าใจการวิเคราะห์บริบท
การทําความเข้าใจบริบทและภูมิหลังทางทฤษฎีของตัวแปรเป็นสิ่งสําคัญสําหรับการตีความผลสหัสทนา
กระได:
- ตรวจสอบตัวแปร: พิจารณาลักษณะและความสัมพันธ์ที่คาดหวังระหว่างตัวแปร
- ใช้ความรู้โดเมน: ใช้ความรู้จากภาคสนามเพื่อตั้งสมมติฐานว่าคาดว่าจะมีความสัมพันธ์หรือไม่
ความสัมพันธ์เป็นศูนย์:
- หากทฤษฎีและการวิจัยก่อนหน้านี้ชี้ให้เห็นว่าไม่มีความสัมพันธ์เชิงตรรกะสิ่งนี้สนับสนุนการค้นพบความสัมพันธ์นี้
ตัวอย่าง:
- กรุ๊ปเลือดและอุบัติการณ์ไข้หวัด: การรู้ว่ากรุ๊ปเลือดไม่ส่งผลต่อความอ่อนไหวต่อไข้หวัดสนับสนุนการตีความความสัมพันธ์เป็นศูนย์หากพบ
สหสัมพันธ์เชิงลบกับบวกกับความสัมพันธ์เป็นศูนย์
สหสัมพันธ์เป็นการวัดทางสถิติที่อธิบายถึงความแข็งแกร่งและทิศทางของความสัมพันธ์ระหว่างตัวแปรสองตัว ต่อไปนี้เป็นคําอธิบายโดยละเอียดเกี่ยวกับความสัมพันธ์เชิงลบ บวก และศูนย์:
ความสัมพันธ์เชิงบวก
- นิยาม: ความสัมพันธ์เชิงบวกเกิดขึ้นเมื่อตัวแปรสองตัวเคลื่อนที่ไปในทิศทางเดียวกัน เมื่อตัวแปรหนึ่งเพิ่มขึ้นตัวแปรอื่นก็เพิ่มขึ้นเช่นกันและเมื่อตัวหนึ่งลดลงตัวแปรอื่นก็ลดลงเช่นกัน
- ตัวอย่าง: ความสัมพันธ์ระหว่างส่วนสูงและน้ําหนัก โดยทั่วไปเมื่อความสูงของบุคคลเพิ่มขึ้นน้ําหนักก็มีแนวโน้มที่จะเพิ่มขึ้นเช่นกัน
- การแสดงกราฟิก: ในแผนภาพกระจาย จุดมักจะกระจุกตัวอยู่รอบเส้นที่ลาดขึ้นจากซ้ายไปขวา
ความสัมพันธ์เชิงลบ
- นิยาม: ความสัมพันธ์เชิงลบเกิดขึ้นเมื่อตัวแปรสองตัวเคลื่อนที่ไปในทิศทางตรงกันข้าม เมื่อตัวแปรหนึ่งเพิ่มขึ้นตัวแปรอื่นจะลดลงและในทางกลับกัน
- ตัวอย่าง: ความสัมพันธ์ระหว่างระยะเวลาที่ใช้ในการศึกษาและจํานวนข้อผิดพลาดที่เกิดขึ้นในการทดสอบ โดยทั่วไปเมื่อเวลาที่ใช้ในการเรียนเพิ่มขึ้นจํานวนข้อผิดพลาดจะลดลง
- การแสดงกราฟิก: ในแผนภาพกระจาย จุดมักจะกระจุกตัวอยู่รอบๆ เส้นที่ลาดลงจากซ้ายไปขวา
สหสัมพันธ์เป็นศูนย์
- นิยาม: บ่งชี้ว่าไม่มีความสัมพันธ์ระหว่างตัวแปรทั้งสอง การเปลี่ยนแปลงในตัวแปรหนึ่งไม่ได้คาดการณ์การเปลี่ยนแปลงในตัวแปรอื่น
- ตัวอย่าง: ความสัมพันธ์ระหว่างขนาดรองเท้าของบุคคลกับความฉลาดทางสติปัญญา (IQ) ไม่มีการเชื่อมต่อเชิงตรรกะระหว่างตัวแปรทั้งสองนี้
- การแสดงกราฟิก: ในพล็อตกระจาย จุดจะกระจายแบบสุ่มโดยไม่มีรูปแบบหรือความชันที่มองเห็นได้
QuestionPro สามารถช่วยในการวิเคราะห์สหสัมพันธ์ได้อย่างไร?
QuestionPro ซึ่งเป็นแพลตฟอร์มการสํารวจที่มีประสิทธิภาพมีเครื่องมือที่ครอบคลุมเพื่ออํานวยความสะดวกในการวิเคราะห์ความสัมพันธ์อย่างมีประสิทธิภาพ นี่คือวิธีที่ QuestionPro สามารถช่วยคุณในการวิเคราะห์สหสัมพันธ์:
การรวบรวมข้อมูลที่ง่ายดาย
QuestionPro ช่วยลดความยุ่งยากในกระบวนการรวบรวมข้อมูลผ่านเครื่องมือสร้างแบบสํารวจที่ใช้งานง่าย คุณสามารถออกแบบและแจกจ่ายแบบสํารวจเพื่อรวบรวมข้อมูลเชิงปริมาณเกี่ยวกับตัวแปรต่างๆ ที่น่าสนใจ แพลตฟอร์มรองรับคําถามประเภทต่างๆ ช่วยให้คุณเก็บข้อมูลโดยละเอียดและเกี่ยวข้องได้อย่างมีประสิทธิภาพ
การวิเคราะห์ข้อมูลอัตโนมัติ
เมื่อรวบรวมข้อมูลแล้ว QuestionPro จะมีเครื่องมือวิเคราะห์ในตัวสําหรับการวิเคราะห์สหสัมพันธ์ คุณสามารถคํานวณความสัมพันธ์ได้อย่างง่ายดาย ซึ่งวัดความแรงและทิศทางของความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว ค่าสัมประสิทธิ์สหสัมพันธ์เชิงเส้นมีตั้งแต่ -1 ถึง 1 โดยที่:
- 1 บ่งชี้ถึงความสัมพันธ์เชิงบวกที่สมบูรณ์แบบ
- -1 หมายถึงความสัมพันธ์เชิงลบที่สมบูรณ์แบบ
- 0 แสดงว่าไม่มีความสัมพันธ์
การแสดงภาพ
QuestionPro มีเครื่องมือสร้างภาพเพื่อช่วยคุณตีความผลลัพธ์ของการวิเคราะห์สหสัมพันธ์ของคุณ สามารถสร้างแผนภาพกระจายและเมทริกซ์สหสัมพันธ์เพื่อให้การแสดงกราฟิกที่ชัดเจนของความสัมพันธ์ระหว่างตัวแปร สื่อช่วยในการมองเห็นนี้มีความสําคัญต่อการระบุแนวโน้มและรูปแบบอย่างรวดเร็ว
การระบุรูปแบบและแนวโน้ม
การใช้การวิเคราะห์สหัสความสัมพันธ์ของ QuestionPro นักวิจัยสังเกตเห็นความสัมพันธ์ (บวก ลบ หรือศูนย์) ระหว่างตัวแปร:
- ความสัมพันธ์เชิงบวก: ตัวแปรทั้งสองเคลื่อนที่ไปในทิศทางเดียวกัน ตัวอย่างเช่น การใช้จ่ายในการโฆษณาที่เพิ่มขึ้นอาจสัมพันธ์กับยอดขายที่เพิ่มขึ้น
- ความสัมพันธ์เชิงลบ: ตัวแปรมีแนวโน้มที่จะเคลื่อนที่ไปในทิศทางตรงกันข้าม ตัวอย่างเช่น เวลาอยู่หน้าจอที่เพิ่มขึ้นอาจสัมพันธ์กับผลการเรียนที่ลดลง
- ความสัมพันธ์เป็นศูนย์: ไม่มีความสัมพันธ์ระหว่างตัวแปร ตัวอย่างเช่น จํานวนปีในโรงเรียนอาจไม่สัมพันธ์กับจํานวนตัวอักษรในชื่อบุคคล
การประยุกต์ใช้จริง
การวิเคราะห์สหสัมพันธ์ใน QuestionPro สามารถใช้สําหรับการใช้งานจริงต่างๆ เช่น:
- การวิจัยตลาด: วัดประสิทธิภาพของแคมเปญการตลาดโดยเชื่อมโยงการใช้จ่ายในการโฆษณากับประสิทธิภาพการขาย
- ดูแล สุขภาพ: ประเมินความสัมพันธ์ระหว่างการใช้ยากับผลลัพธ์ของผู้ป่วย เช่น ระดับความดันโลหิต
- การศึกษา: กําหนดผลกระทบของพฤติกรรมการเรียนต่อผลการเรียนโดยเชื่อมโยงชั่วโมงเรียนกับเกรด
บทสรุป
ความสัมพันธ์เป็นศูนย์ระหว่างตัวแปรสองตัวแสดงถึงการไม่มีความสัมพันธ์เชิงเส้นซึ่งบ่งชี้ว่าการเปลี่ยนแปลงในตัวแปรหนึ่งไม่สอดคล้องกับการเปลี่ยนแปลงในอีกตัวแปรหนึ่ง ด้วยการคํานวณค่าสัมประสิทธิ์สหสัมพันธ์และการแสดงภาพข้อมูลผ่านแผนภาพกระจายนักวิจัยสามารถระบุได้อย่างแม่นยําว่าตัวแปรมีความสัมพันธ์กันมีความสัมพันธ์เชิงบวกความสัมพันธ์เชิงลบหรือแสดงความสัมพันธ์นี้
การใช้ QuestionPro สําหรับการวิเคราะห์สหสัมพันธ์ในแบบสํารวจของคุณเป็นวิธีที่มีประสิทธิภาพในการเปิดเผยความสัมพันธ์ที่มีความหมายระหว่างตัวแปร ด้วยการสํารวจอินเทอร์เฟซที่ใช้งานง่ายของ QuestionPro เครื่องมือวิเคราะห์ขั้นสูง และคุณสมบัติการรายงานที่ครอบคลุม คุณจะสามารถทําการวิเคราะห์สหสัมพันธ์ได้อย่างมีประสิทธิภาพและรับข้อมูลเชิงลึกอันมีค่าจากข้อมูลของคุณ ติดต่อ QuestionPro วันนี้เพื่อขอข้อมูลเพิ่มเติม!







