ค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน: สูตรและตัวอย่าง

เป็นเรื่องปกติที่จะหาปริมาณความสัมพันธ์เชิงเส้นผ่านค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สัน เพื่อระบุความแรงและทิศทางของการเชื่อมต่อระหว่างตัวแปรสองตัวจะใช้ค่าระหว่าง -1 ถึง 1

สามารถช่วยให้นักลงทุนกระจายความเสี่ยงได้ การคํานวณจากแผนภาพกระจายของผลตอบแทนในอดีตระหว่างคู่สินทรัพย์ เช่น หุ้น-พันธบัตร หุ้น-สินค้าโภคภัณฑ์ พันธบัตร-อสังหาริมทรัพย์ ฯลฯ จะช่วยให้นักลงทุนสร้างพอร์ตการลงทุนความเสี่ยง-ผลตอบแทน

ดังนั้นเราจะได้เรียนรู้เกี่ยวกับค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันและรู้วิธีวัดความสัมพันธ์ระหว่างตัวแปรที่เกี่ยวข้องสองตัวโดยใช้มัน

ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันคืออะไร?

ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันหรือค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันหรือ r ของเพียร์สันถูกกําหนดไว้ในสถิติว่าเป็นการวัดความแข็งแกร่งของความสัมพันธ์ระหว่างตัวแปรสองตัวและความเชื่อมโยงซึ่งกันและกัน

พูดง่ายๆ ก็คือ ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันจะคํานวณผลกระทบของการเปลี่ยนแปลงในตัวแปรหนึ่งเมื่อตัวแปรอื่นเปลี่ยนแปลง

เช่น จนถึงอายุที่กําหนด (ในกรณีส่วนใหญ่) ความสูงของเด็กจะเพิ่มขึ้นเรื่อย ๆ เมื่ออายุของเขา/เธอเพิ่มขึ้น แน่นอนว่าการเติบโตของเขา/เธอขึ้นอยู่กับปัจจัยต่างๆ เช่น ยีน สถานที่ อาหาร ไลฟ์สไตล์ ฯลฯ

วิธีนี้ขึ้นอยู่กับความแปรปรวนร่วม ดังนั้นจึงเป็นวิธีที่ดีที่สุดในการวัดความสัมพันธ์ระหว่างตัวแปรสองตัว

เมื่อใดควรใช้ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สัน

สหสัมพันธ์ค่าสัมประสิทธิ์เพียร์สันมีความสําคัญทางสถิติสูง มันดูความสัมพันธ์ระหว่างสองตัวแปร พยายามขีดเส้นผ่านข้อมูลของตัวแปรสองตัวเพื่อแสดงความสัมพันธ์ของพวกเขา ความสัมพันธ์ของตัวแปรวัดด้วยความช่วยเหลือของเครื่องคํานวณค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน ความสัมพันธ์เชิงเส้นนี้อาจเป็นบวกหรือลบ

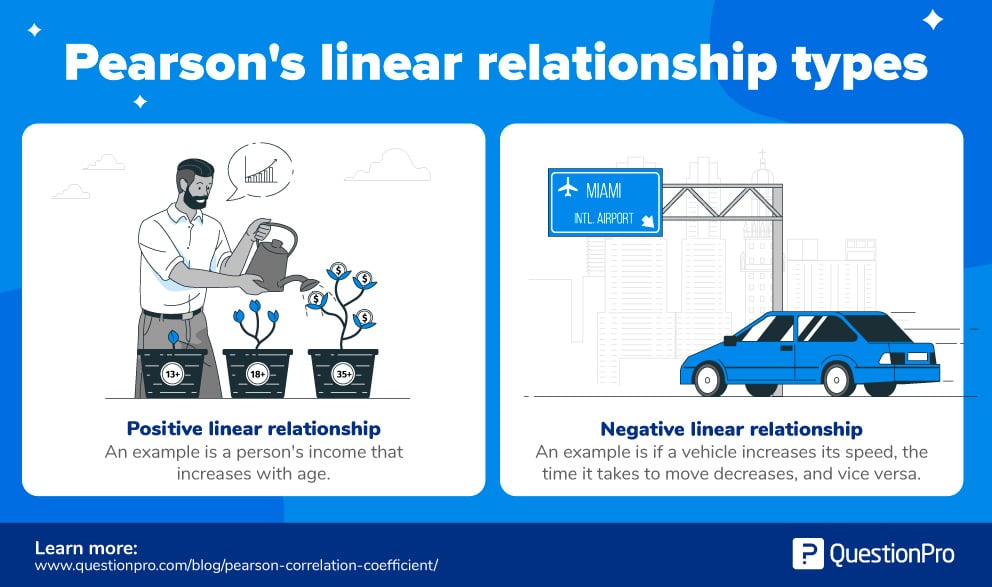
เช่น:

• ความสัมพันธ์เชิงเส้นเชิงบวก: ในกรณีส่วนใหญ่ รายได้ของบุคคลจะเพิ่มขึ้นเมื่ออายุของเขา/เธอเพิ่มขึ้น
• ความสัมพันธ์เชิงเส้นเชิงลบ: หากรถเพิ่มความเร็ว เวลาที่ใช้ในการเดินทางจะลดลง และในทางกลับกัน

จากตัวอย่างข้างต้น จะเห็นได้ชัดว่าค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สัน r พยายามค้นหาสองสิ่ง – ความแข็งแกร่งและทิศทางของความสัมพันธ์จากขนาดตัวอย่างที่กําหนด

สูตรค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันและการคํานวณ

สูตรค่าสัมประสิทธิ์สหสัมพันธ์จะหาความสัมพันธ์ระหว่างตัวแปร ส่งคืนค่าระหว่าง -1 ถึง 1 ใช้เครื่องคํานวณสหสัมพันธ์ค่าสัมประสิทธิ์เพียร์สันด้านล่างเพื่อวัดความแข็งแกร่งของตัวแปรสองตัว

สูตรสัมประสิทธิ์สหสัมพันธ์เพียร์สัน:

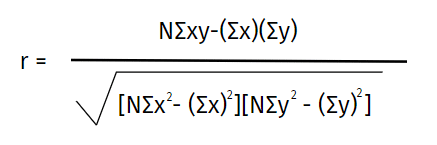
ที่ไหน:
N = จํานวนคู่ของคะแนน
Σxy = ผลรวมของผลคูณของคะแนนคู่
Σx = ผลรวมของคะแนน x
Σy = ผลรวมของคะแนน Y
Σx2 = ผลรวมของคะแนนกําลังสอง x
Σy2 = ผลรวมของคะแนน y กําลังสอง

การคำนวณ

นี่คือคําแนะนําทีละขั้นตอนในการคํานวณค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สัน:

ขั้นตอนที่หนึ่ง: สร้างตารางค่าสัมประสิทธิ์สหสัมพันธ์
สร้างแผนภูมิข้อมูลรวมถึงตัวแปรทั้งสอง ติดป้ายกํากับตัวแปรเหล่านี้ ‘x’ และ ‘y’ เพิ่มคอลัมน์เพิ่มเติมสามคอลัมน์ ได้แก่ (xy), (x^2) และ (y^2) อ้างถึงแผนภูมิข้อมูลอย่างง่ายนี้

ขั้นตอนที่สอง: ใช้การคูณพื้นฐานเพื่อทําให้ตารางสมบูรณ์

ขั้นตอนที่สาม: เพิ่มคอลัมน์ทั้งหมดจากล่างขึ้นบน

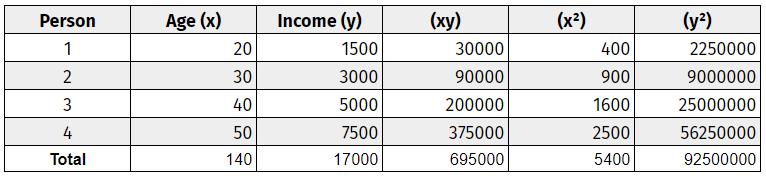
ขั้นตอนที่สี่: ใช้สูตรสหสัมพันธ์เพื่อเสียบค่า

หากผลลัพธ์เป็นลบ แสดงว่ามี ความสัมพันธ์เชิงลบ ระหว่างตัวแปรทั้งสอง หากผลลัพธ์เป็นบวก แสดงว่ามีความสัมพันธ์เชิงบวกระหว่างตัวแปร ผลลัพธ์ยังสามารถกําหนดความแข็งแกร่งของความสัมพันธ์เชิงเส้น เช่น ความสัมพันธ์เชิงบวกที่แข็งแกร่ง ความสัมพันธ์เชิงลบที่แข็งแกร่ง ความสัมพันธ์เชิงบวกปานกลาง และอื่นๆ

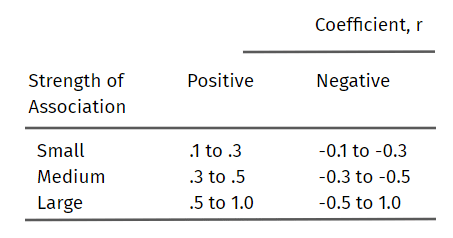
การกําหนดความแข็งแรงของค่าสัมประสิทธิ์สหสัมพันธ์โมเมนต์ผลิตภัณฑ์เพียร์สัน

ค่าสัมประสิทธิ์สหสัมพันธ์โมเมนต์ผลิตภัณฑ์เพียร์สัน หรือเพียงแค่ค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สันหรือสหสัมพันธ์ค่าสัมประสิทธิ์เพียร์สัน r กําหนดความแข็งแกร่งของความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว

ยิ่งความสัมพันธ์ระหว่างตัวแปรทั้งสองแข็งแกร่งเท่าใด คําตอบของคุณก็จะยิ่งเอียงไปทาง 1 หรือ -1 มากขึ้นเท่านั้น การได้ค่า 1 หรือ -1 แสดงว่าจุดข้อมูลทั้งหมดถูกพล็อตบนเส้นตรงของ ‘เหมาะสมที่สุด’ หมายความว่าการเปลี่ยนแปลงของปัจจัยของตัวแปรใด ๆ ไม่ได้ทําให้ความสัมพันธ์กับตัวแปรอื่นอ่อนแอลง ยิ่งคําตอบของคุณอยู่ใกล้ 0 มากเท่าไหร่ตัวแปรก็จะยิ่งมีความแปรปรวนมากขึ้นเท่านั้น

จะตีความค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันได้อย่างไร?

ด้านล่างนี้คือแนวทางที่เสนอสําหรับการตีความสัมประสิทธิ์สัมประสิทธิ์เพียร์สัน:

โปรดทราบว่าความแข็งแกร่งของการเชื่อมโยงของตัวแปรขึ้นอยู่กับสิ่งที่คุณวัดและขนาดตัวอย่าง

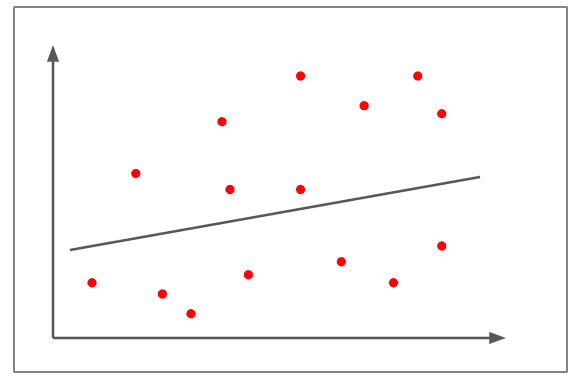
บนกราฟเราสามารถสังเกตเห็นความสัมพันธ์ระหว่างตัวแปรและตั้งสมมติฐานก่อนที่จะคํานวณได้ แผนภูมิกระจายหากอยู่ใกล้กับเส้นจะแสดงความสัมพันธ์ที่แน่นแฟ้นระหว่างตัวแปร

ยิ่งพล็อตกระจายอยู่ใกล้กับเส้นมากเท่าใดความสัมพันธ์ระหว่างตัวแปรก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น ยิ่งพวกเขาย้ายออกจากเส้นมากเท่าไหร่ความสัมพันธ์ก็ยิ่งอ่อนแอลงเท่านั้น หากเส้นเกือบขนานกับแกน x เนื่องจากแผนภูมิกระจายที่สุ่มวางอยู่บนกราฟ ก็ปลอดภัยที่จะสันนิษฐานว่าไม่มีความสัมพันธ์ระหว่างตัวแปรทั้งสอง

คําว่า Strength และ Direction หมายถึงอะไร?

คําว่า ‘ความแข็งแกร่ง’ และ ‘ทิศทาง’ มีความสําคัญทางสถิติ นี่คือคําอธิบายที่ตรงไปตรงมาของคําสองคํา:

• แรง: ความแข็งแกร่งหมายถึงความสัมพันธ์ระหว่างตัวแปรสองตัว หมายความว่าตัวแปรหนึ่งจะเปลี่ยนแปลงอย่างสม่ําเสมอเพียงใดเนื่องจากการเปลี่ยนแปลงของอีกตัวแปรหนึ่ง ค่าที่ใกล้เคียงกับ +1 หรือ -1 บ่งชี้ถึงความสัมพันธ์ที่แน่นแฟ้น ค่าเหล่านี้จะได้หากจุดข้อมูลตกลงบนหรืออยู่ใกล้กับเส้นมาก
  
  ยิ่งจุดข้อมูลเคลื่อนออกไปมากเท่าใด ความแข็งแกร่งของความสัมพันธ์เชิงเส้นก็จะยิ่งอ่อนแอลงเท่านั้น เมื่อไม่มีวิธีปฏิบัติในการวาดเส้นตรงเนื่องจากจุดข้อมูลกระจัดกระจายความแข็งแกร่งของความสัมพันธ์เชิงเส้นจะอ่อนแอที่สุด
• ทิศทาง: ทิศทางของเส้นบ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงเส้นเชิงบวกหรือเชิงลบระหว่างตัวแปร หากเส้นมีความชันขึ้นตัวแปรจะมีความสัมพันธ์เชิงบวก
  
  ซึ่งหมายความว่าการเพิ่มมูลค่าของตัวแปรหนึ่งจะนําไปสู่การเพิ่มมูลค่าของตัวแปรอื่น ความสัมพันธ์เชิงลบแสดงให้เห็นถึงความลาดชันลง ซึ่งหมายความว่าการเพิ่มขึ้นของปริมาณของตัวแปรหนึ่งนําไปสู่การลดลงของมูลค่าของตัวแปรอื่น

ตัวอย่างค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน

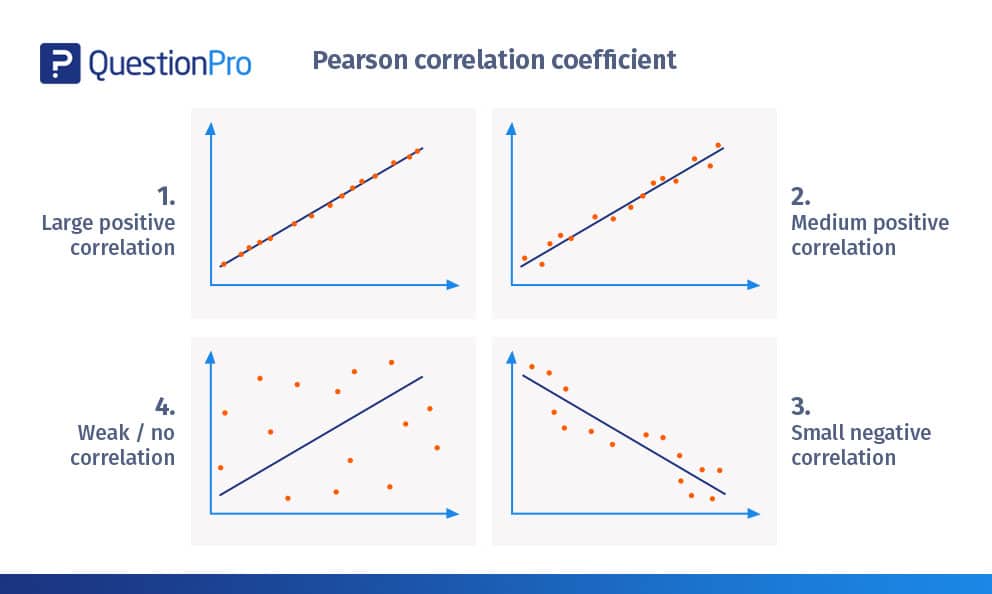
ลองดูตัวอย่างภาพเพื่อช่วยคุณตีความตารางค่าสัมประสิทธิ์สหสัมพันธ์:

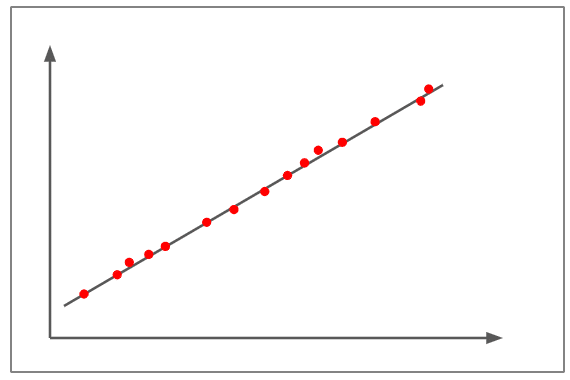
ความสัมพันธ์เชิงบวกขนาดใหญ่

• รูปด้านบนแสดงให้เห็นถึงความสัมพันธ์เกือบ +1
• แผนภาพกระจายเกือบจะพล็อตเป็นเส้นตรง
• ความชันเป็นบวกซึ่งหมายความว่าหากตัวแปรหนึ่งเพิ่มขึ้นตัวแปรอื่นก็เพิ่มขึ้นเช่นกันโดยแสดงเส้นเชิงเส้นที่เป็นบวก
• สิ่งนี้แสดงว่าการเปลี่ยนแปลงในตัวแปรหนึ่งเป็นสัดส่วนโดยตรงกับการเปลี่ยนแปลงในตัวแปรอื่น
• ตัวอย่างของความสัมพันธ์เชิงบวกขนาดใหญ่คือ – เมื่อเด็กโตขึ้นเสื้อผ้าและขนาดรองเท้าก็เช่นกัน

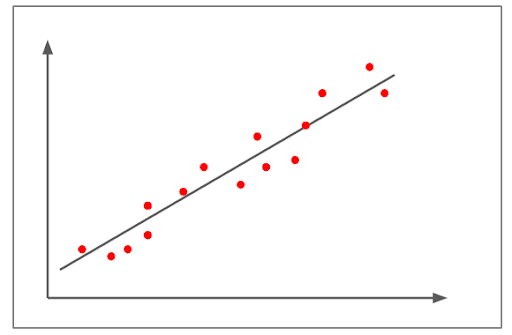
ความสัมพันธ์เชิงบวกปานกลาง

• รูปด้านบนแสดงความสัมพันธ์เชิงบวก
• ความสัมพันธ์สูงกว่า +0.8 แต่ต่ํากว่า 1+
• มันแสดงให้เห็นรูปแบบการขึ้นเนินเชิงเส้นที่ค่อนข้างแข็งแกร่ง
• ตัวอย่างของความสัมพันธ์เชิงบวกปานกลางคือ – เมื่อจํานวนรถยนต์เพิ่มขึ้นความต้องการตัวแปรเชื้อเพลิงก็เพิ่มขึ้นเช่นกัน

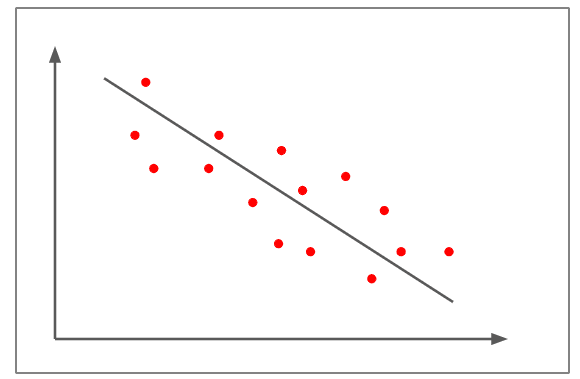
ความสัมพันธ์เชิงลบขนาดเล็ก

• ในรูปด้านบน แผนภาพกระจายไม่ใกล้เคียงกับเส้นตรงเมื่อเทียบกับตัวอย่างก่อนหน้านี้
• แสดงสหสัมพันธ์เชิงเส้นเชิงลบประมาณ -0.5
• การเปลี่ยนแปลงในตัวแปรหนึ่งเป็นสัดส่วนผกผันกับการเปลี่ยนแปลงของตัวแปรอื่น เนื่องจากความชันเป็นลบ
• ตัวอย่างของความสัมพันธ์เชิงลบเล็กน้อยคือยิ่งมีคนกินมากเท่าไหร่ก็ยิ่งหิวน้อยลงเท่านั้น

อ่อนแอ / ไม่มีความสัมพันธ์

• แผนภาพกระจายอยู่ไกลจากเส้น
• เป็นการยากที่จะลากเส้นในทางปฏิบัติ
• ความสัมพันธ์อยู่ที่ประมาณ +0.15
• ไม่สามารถตัดสินได้ว่าการเปลี่ยนแปลงในตัวแปรหนึ่งเป็นสัดส่วนโดยตรงหรือแปรผกผันกับตัวแปรอื่น
• ตัวอย่างของความสัมพันธ์ที่อ่อนแอ/ไม่มีเลยคือการเพิ่มขึ้นของราคาน้ํามันเชื้อเพลิงทําให้ผู้คนรับเลี้ยงสัตว์เลี้ยงน้อยลง

ความสัมพันธ์ของ T-Test กับ Pearson: อะไรคือความแตกต่าง?

เมื่อวิเคราะห์ข้อมูล สิ่งสําคัญคือต้องเลือกวิธีการทางสถิติที่เหมาะสมตามสิ่งที่คุณพยายามบรรลุ การทดสอบ T และความสัมพันธ์ของเพียร์สันอาจดูคล้ายกัน แต่มีจุดประสงค์ที่แตกต่างกัน:

• การทดสอบที: ใช้เพื่อเปรียบเทียบค่าเฉลี่ยของสองกลุ่มและพิจารณาว่าต่างกันอย่างมีนัยสําคัญหรือไม่
• ความสัมพันธ์ของเพียร์สัน: วัดความแข็งแกร่งและทิศทางของความสัมพันธ์ระหว่างตัวแปรต่อเนื่องสองตัว

พูดง่ายๆ ก็คือ ใช้การทดสอบ T เมื่อเปรียบเทียบกลุ่ม และใช้สหสัมพันธ์ของเพียร์สันเมื่อสํารวจความสัมพันธ์ระหว่างตัวแปร การทําความเข้าใจความแตกต่างช่วยให้คุณตัดสินใจโดยใช้ข้อมูลได้ดียิ่งขึ้น!

คําพูดสุดท้ายเกี่ยวกับ r ของเพียร์สัน

ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันสามารถกําหนดได้โดยการรวบรวมข้อมูลเกี่ยวกับตัวแปรสองตัวที่น่าสนใจผ่านการสํารวจ คุณสามารถใช้สิ่งนี้เพื่อเรียนรู้ว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองเป็นบวกหรือลบ และแข็งแกร่งแค่ไหน

QuestionPro Research Suite เป็นชุดเครื่องมือในการใช้ประโยชน์จากการวิจัยและเปลี่ยนข้อมูลเชิงลึกที่สามารถใช้เพื่อรวบรวมข้อมูลสําหรับการวิเคราะห์ค่าสัมประสิทธิ์สหสัมพันธ์ของ Pearson หลังจาก ส่งออกข้อมูลแบบสํารวจ จาก QuestionPro และนําเข้าไปยังสเปรดชีตหรือแอปพลิเคชันทางสถิติแล้ว คุณสามารถทําการวิเคราะห์สหสัมพันธ์ได้

QuestionPro นําเสนอเครื่องมือวิเคราะห์ข้อมูลที่เป็นประโยชน์ เช่น การตารางข้าม การแสดงข้อมูล และการทดสอบทางสถิติ นอกเหนือจากการคํานวณค่าสัมประสิทธิ์สหสัมพันธ์ คุณสมบัติเหล่านี้สามารถช่วยในการวิจัยและทําความเข้าใจความสัมพันธ์ระหว่างตัวแปรของคุณ

พร้อมที่จะค้นพบความสัมพันธ์ระหว่างตัวแปรของคุณและพัฒนาการวิเคราะห์ข้อมูลของคุณแล้วหรือยัง เริ่มทดลองใช้ QuestionPro ฟรีวันนี้เพื่อดูว่าซอฟต์แวร์สํารวจของเราสามารถช่วยคุณกําหนดค่าสัมประสิทธิ์สหสัมพันธ์ของ Pearson ได้อย่างง่ายดายได้อย่างไร อย่าพลาดโอกาสนี้ในการปรับปรุงการวิเคราะห์ข้อมูลและการวิจัย

เรียนรู้เพิ่มเติม ทดลองใช้ฟรี

คําถามที่พบบ่อย