
Korelasyon, istatistik ve veri analizinde iki değişken arasındaki ilişkiyi anlamaya yardımcı olan temel bir kavramdır. Güçlü pozitif veya negatif korelasyonlar genellikle vurgulanırken, sıfır korelasyon da aynı derecede önemlidir.
Bu, değişkenler arasında doğrusal bir ilişki olmadığı anlamına gelir. Başka bir deyişle, bir değişkendeki değişiklikler diğerindeki değişiklikleri öngörmez.
Bu blogda, net bir tanım, açıklayıcı örnekler ve bunu belirleme yöntemleri sunarak sıfır korelasyon kavramını inceleyeceğiz.
Sıfır Korelasyon nedir?
Sıfır korelasyon, iki değişken arasında doğrusal bir ilişkinin olmadığı bir durumu tanımlayan istatistiksel bir terimdir. İki değişken sıfır korelasyona sahip olduğunda, bir değişkendeki değişiklikler diğerindeki değişiklikleri öngörmez. Değişkenler arasındaki ilişkinin derecesini ve yönünü ölçen korelasyon katsayısı bu durumda tam olarak sıfırdır.
Bu korelasyonu anlamak istatistiksel analizde önemlidir, çünkü birbirleriyle tahmin edici bir ilişkisi olmayan değişkenleri belirlemeye yardımcı olur, bu da istatistiksel modeller oluştururken veya veri modellerini yorumlarken çok önemlidir.
Sıfır Korelasyon neden önemlidir?
Sıfır korelasyon, istatistik ve veri analizinde çeşitli nedenlerden dolayı önemli bir kavramdır:
Bağımsızlığı Tanımlar
Birbirinden doğrusal olarak bağımsız olan değişkenlerin belirlenmesine yardımcı olur. İki değişken arasında sıfır korelasyon varsa, bir değişkendeki değişiklikler diğerindeki değişiklikler hakkında herhangi bir bilgi sağlamaz. Bu, verilerin yapısını ve değişkenler arasındaki ilişkileri (veya bunların eksikliğini) anlamak için çok önemlidir.
İstatistiksel Modelleri Geliştirir
Regresyon analizinde ve diğer istatistiksel modellerde, bağımlı değişkenle bu korelasyona sahip değişkenlerin dahil edilmesi gürültü ekleyebilir ve modelin tahmin gücünü azaltabilir. Bu tür değişkenlerin belirlenmesi ve hariç tutulmasıyla modeller basitleştirilebilir ve daha verimli hale getirilerek daha iyi performans ve yorumlanabilirlik sağlanabilir.
Bu Korelasyon Yanlış Yorumlamaların Önlenmesine Yardımcı Olur
Bu korelasyonun anlaşılması verilerin yanlış yorumlanmasını önler.
- Örneğin, bir araştırmacı sezgilerine veya ilk gözlemlerine dayanarak iki değişken arasında yanlışlıkla bir ilişki çıkarabilir.
Korelasyon katsayısının hesaplanması ve sıfır olarak bulunması, doğrusal bir ilişkinin olmadığını açıklığa kavuşturur ve yanlış sonuçlara varılmasını önler.
Doğrusal Olmayan İlişkileri Vurguluyor
Doğrusal olmayan ilişkiler olasılığını vurgular. İki değişken arasında sıfır korelasyon varsa, bu mutlaka ilişkisiz oldukları anlamına gelmez; karmaşık, doğrusal olmayan bir ilişkiye sahip olabilirler. Bunun farkına varmak, doğrusal olmayan regresyon veya veri dönüşümleri gibi diğer yöntemleri kullanarak daha fazla araştırma yapılmasını sağlayabilir.
Korelasyon Deneysel Tasarımın Yönlendirilmesine Yardımcı Olur
Deneysel tasarımda, hangi değişkenlerin sıfır korelasyona sahip olduğunu bilmek, dahil edilecek veya kontrol edilecek değişkenlerin seçimine rehberlik edebilir. Bu, ilgisiz değişkenlerin etkisinin en aza indirildiği daha sağlam deneylerin tasarlanmasına yardımcı olarak daha net, daha güvenilir sonuçlar elde edilmesini sağlar.
Değişken Davranışları Anlar
Bir veri kümesindeki değişkenlerin davranışları hakkında içgörü sağlar. Finansal analizde, hangi varlıkların birbirleriyle sıfır korelasyona sahip olduğunu anlamak, portföy çeşitlendirmesine yardımcı olabilir, çünkü bu tür varlıkları birleştirmek genel riski azaltabilir.
Hipotez Testlerini Destekler
Hipotez testlerinde bu korelasyon genellikle boş hipotezdir.
- Örneğin, iki değişkenin ilişkili olup olmadığını test ederken, sıfır hipotezi aralarındaki korelasyonun sıfır olduğunu belirtebilir.
Bunun doğru ya da yanlış olduğunun belirlenmesi, hipotezlerin doğrulanmasına ya da çürütülmesine yardımcı olur.
Sıfır Korelasyon Örnekleri Nelerdir?
Bir değişkendeki değişikliklerin başka bir değişkendeki değişikliklere karşılık gelmediği bu korelasyonun örneklerine çeşitli alanlarda rastlanabilir:
Araştırma Alanı
Örnek: Bilimsel Yayın Sayısı ve En Sevilen Dondurma Lezzeti
Bir araştırma, bir araştırmacının sahip olduğu bilimsel yayın sayısı ile en sevdiği dondurma aroması arasındaki ilişkiyi inceliyor.
Bir araştırmacının yayınladığı bilimsel makale sayısı ile belirli bir dondurma aromasını tercih etmesi arasında mantıksal bir bağlantı yoktur. Sonuç olarak, bu iki değişkenin bu korelasyonu göstermesi beklenmektedir.
Eğitim Alanı
Örnek: Öğrencilerin Ayakkabı Numarası ve Matematik Notları
Bir eğitim araştırması, öğrencilerin ayakkabı numaraları ile matematik notları arasında herhangi bir ilişki olup olmadığını incelemektedir.
Ayakkabı numarası, bir öğrencinin matematikteki akademik performansı üzerinde hiçbir etkisi olmayan fiziksel bir özelliktir. Bu nedenle, ayakkabı numarası ile matematik notları arasındaki korelasyonun sıfır olması muhtemeldir.
Sağlık Hizmetleri Alanı
Örnek: Kan Grubu ve Soğuk Algınlığı İnsidansı
Bir sağlık araştırması, kişinin kan grubu ile bir yıl içinde soğuk algınlığına yakalanma sayısı arasında bir ilişki olup olmadığını inceliyor.
Kan grubu, virüslere maruz kalma ve bağışıklık sistemi gücü gibi çeşitli diğer faktörlerden etkilenen soğuk algınlığına yakalanma sıklığı ile ilişkili değildir. Dolayısıyla, kan grubu ile soğuk algınlığı görülme sıklığı arasındaki korelasyonun sıfır olması beklenir.
Sıfır Korelasyon Nasıl Belirlenir?
Burada, görsel inceleme, istatistiksel hesaplama, hipotez testi ve bağlamsal analiz yoluyla bu korelasyonun nasıl belirleneceğini keşfedeceğiz.
1. Dağılım Grafikleri Kullanılarak Görsel İnceleme
Dağılım grafikleri, iki değişken arasındaki ilişkiyi görsel olarak değerlendirmek için etkili bir araçtır.
Bir Dağılım Grafiği Oluşturun:
- Değişkenlerden birini x eksenine, diğerini y eksenine yerleştirin.
- Veri noktalarında fark edilebilir bir eğilim veya model olup olmadığına bakın.
Korelasyonun Belirlenmesi:
- Eğer noktalar net bir eğilim olmadan (ne yukarı ne de aşağı) rastgele dağılmışsa, bu korelasyon olduğunu gösterir.
- Rastgele bir dağılım, hiçbir doğrunun (ister düz ister eğri olsun) veri noktalarına iyi uyamayacağı anlamına gelir.
Örnek:
- Öğrencilerin Ayakkabı Numaraları ve Matematik Notları: Ayakkabı numaralarını matematik notlarına karşı çizerseniz ve hiçbir eğilim olmadan rastgele bir nokta dağılımı görürseniz, bu sıfır korelasyon olduğunu gösterir.
2. Korelasyon Katsayısını Hesaplayın
Pearson korelasyon katsayısı (r) doğrusal korelasyonun en yaygın ölçüsüdür.
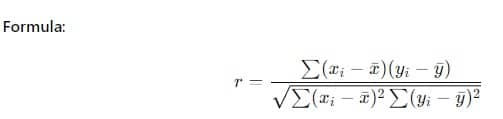
Adımlar:
- İki değişken için eşleştirilmiş veri noktaları toplayın.
- Her bir değişkenin ortalamasını bulun.
- Her bir veri noktasının ortalamadan ne kadar uzakta olduğunu hesaplayın.
- Her bir çift için sapmaları çarpın ve çarpımları toplayın.
- Korelasyon katsayısını bulmak için formülü kullanın.
Korelasyonu Yorumlama:
0’a Yakın Değer: 𝑟 r 0’a yakınsa, değişkenler arasında doğrusal ilişkinin çok az olduğunu veya hiç olmadığını gösterir.
Örnek:
- Ayakkabı Numaraları ve Matematik Notları: Hesaplanan 𝑟 yaklaşık olarak 0 ise, sıfır korelasyonu doğrular.
3. Hipotez Testini Yapın
İstatistiksel hipotez testi, gözlemlenen bir korelasyon katsayısının sıfırdan önemli ölçüde farklı olup olmadığını belirleyebilir.
Adımlar:
- Boş Hipotez: Korelasyon katsayısının sıfır olduğunu varsayın.
- Alternatif Hipotez: Korelasyon katsayısının sıfır olmadığını varsayalım.
- Test İstatistiğini Hesaplayın: Korelasyon katsayısı için bir t-testi kullanın.
- P-değerini belirleyin: p-değerini bir anlamlılık düzeyi ile karşılaştırın (örneğin, 0,05).
Sıfır Korelasyon:
- Eğer p-değeri anlamlılık düzeyinden büyükse, boş hipotezi reddetmeyin, bu da korelasyonun sıfırdan önemli ölçüde farklı olmadığını gösterir.
Örnek:
- Kan Grubu ve Soğuk Algınlığı İnsidansı: Kan grubu ile soğuk algınlığı insidansı arasındaki korelasyonun test edilmesi, p-değerinin yüksek olması durumunda, gözlemlenen herhangi bir korelasyonun istatistiksel olarak anlamlı olmadığını gösterir ve sıfır korelasyonu destekler.
4. Bağlamsal Analizi Anlamak
Değişkenlerin bağlamını ve teorik arka planını anlamak, korelasyon sonuçlarını yorumlamak için gereklidir.
Adımlar:
- Değişkenleri İnceleyin: Değişkenler arasındaki doğayı ve beklenen ilişkileri göz önünde bulundurun.
- Alan Bilgisini Uygulayın: Bir ilişkinin beklenip beklenmediğini varsaymak için alandan gelen bilgileri kullanın.
Sıfır Korelasyon:
- Teori ve önceki araştırmalar mantıksal bir ilişkiye işaret etmiyorsa, bu korelasyon bulgusunu desteklemektedir.
Örnek:
- Kan Grubu ve Soğuk Algınlığı İnsidansı: Kan grubunun soğuk algınlığına yatkınlığı etkilemediğinin bilinmesi, bulunması halinde sıfır korelasyon yorumunu destekler.
Negatif vs Pozitif Korelasyon vs Sıfır Korelasyon
Korelasyon, iki değişken arasındaki ilişkinin gücünü ve yönünü tanımlayan istatistiksel bir ölçüdür. Burada negatif, pozitif ve sıfır korelasyonun ayrıntılı bir açıklamasını bulabilirsiniz:
Pozitif Korelasyon
- Tanım: İki değişken aynı yönde hareket ettiğinde pozitif korelasyon oluşur. Bir değişken arttıkça diğer değişken de artar ve biri azaldıkça diğeri de azalır.
- Örnek: Boy ve kilo arasındaki ilişki. Genel olarak, bir kişinin boyu arttıkça, kilosu da artma eğilimindedir.
- Grafiksel Gösterim: Bir dağılım grafiğinde, noktalar soldan sağa doğru yukarı eğimli bir çizgi etrafında kümelenme eğilimindedir.
Negatif Korelasyon
- Tanım: İki değişken zıt yönlerde hareket ettiğinde negatif korelasyon oluşur. Bir değişken arttıkça, diğer değişken azalır veya tam tersi olur.
- Örnek: Çalışmak için harcanan zaman ile bir sınavda yapılan hata sayısı arasındaki ilişki. Genel olarak, ders çalışmak için harcanan zaman arttıkça hata sayısı azalır.
- Grafiksel Gösterim: Bir dağılım grafiğinde, noktalar soldan sağa doğru aşağı eğimli bir çizgi etrafında kümelenme eğilimindedir.
Sıfır Korelasyon
- Tanım: İki değişken arasında bir ilişki olmadığını gösterir. Bir değişkendeki değişiklikler diğer değişkendeki değişiklikleri öngörmez.
- Örnek: Bir kişinin ayakkabı numarası ile zeka bölümü (IQ) arasındaki ilişki. Bu iki değişken arasında mantıksal bir bağlantı yoktur.
- Grafiksel Temsil: Bir dağılım grafiğinde, noktalar fark edilebilir bir desen veya eğim olmaksızın rastgele dağıtılır.
QuestionPro Korelasyon Analizine Nasıl Yardımcı Olabilir?
Sağlam bir anket platformu olan QuestionPro, korelasyon analizini etkili bir şekilde kolaylaştırmak için kapsamlı araçlar sunar. İşte QuestionPro’nun korelasyon analizi yapmanıza nasıl yardımcı olabileceği:
Zahmetsiz Veri Toplama
QuestionPro, kullanıcı dostu anket oluşturma araçlarıyla veri toplama sürecini basitleştirir. İlgilendiğiniz çeşitli değişkenler hakkında nicel veriler toplamak için anketler tasarlayabilir ve dağıtabilirsiniz. Platform, çeşitli soru türlerini destekleyerek ayrıntılı ve ilgili verileri verimli bir şekilde yakalamanıza olanak tanır.
Otomatik Veri Analizi
Veriler toplandıktan sonra, QuestionPro korelasyon analizi için yerleşik analitik araçlar sağlar. İki değişken arasındaki doğrusal ilişkinin gücünü ve yönünü ölçen korelasyonları kolayca hesaplayabilirsiniz. Doğrusal korelasyon katsayısı -1 ile 1 arasında değişir, burada:
- 1 mükemmel pozitif korelasyonu gösterir.
- -1 mükemmel bir negatif korelasyonu gösterir.
- 0 korelasyon olmadığını gösterir.
Görsel Temsil
QuestionPro, korelasyon analizinizin sonuçlarını yorumlamanıza yardımcı olacak görselleştirme araçları sunar. Değişkenler arasındaki ilişkilerin net bir grafiksel gösterimini sağlamak için dağılım grafikleri ve korelasyon matrisleri oluşturulabilir. Bu görsel yardım, eğilimleri ve kalıpları hızlı bir şekilde tanımlamak için çok önemlidir.
Örüntü ve Eğilimlerin Belirlenmesi
Araştırmacılar, QuestionPro’nun korelasyon analizini kullanarak değişkenler arasındaki korelasyonu (pozitif, negatif veya sıfır) gözlemlemişlerdir:
- Pozitif Korelasyon: Her iki değişken de aynı yönde hareket eder. Örneğin, artan reklam harcamaları artan satışlarla ilişkili olabilir.
- Negatif Korelasyon: Değişkenler zıt yönlerde hareket etme eğilimindedir. Örneğin, ekran başında geçirilen sürenin artması akademik performansın düşmesi ile ilişkili olabilir.
- Sıfır Korelasyon: Değişkenler arasında hiçbir ilişki yoktur. Örneğin, okuldaki yıl sayısı bir kişinin ismindeki harf sayısı ile ilişkili olmayabilir.
Pratik Uygulamalar
QuestionPro’daki korelasyon analizi, aşağıdakiler gibi çeşitli pratik uygulamalar için kullanılabilir:
- Pazar Araştırması: Reklam harcamalarını satış performansı ile ilişkilendirerek pazarlama kampanyalarının etkinliğini ölçün.
- Sağlık Hizmetleri: İlaç kullanımı ile kan basıncı seviyeleri gibi hasta sonuçları arasındaki ilişkiyi değerlendirin.
- Eğitim: Çalışılan saatler ile notları ilişkilendirerek çalışma alışkanlıklarının akademik performans üzerindeki etkisini belirleyin.
Sonuç
İki değişken arasındaki sıfır korelasyon, doğrusal bir ilişkinin yokluğunu ifade eder ve bir değişkendeki değişikliklerin diğerindeki değişikliklere karşılık gelmediğini gösterir. Korelasyon katsayılarını hesaplayarak ve verileri dağılım grafikleri aracılığıyla görselleştirerek, araştırmacılar değişkenlerin korelasyonlu, pozitif korelasyonlu, negatif korelasyonlu olup olmadığını veya bu korelasyonu gösterip göstermediğini doğru bir şekilde belirleyebilirler.
Anketlerinizde korelasyon analizi için QuestionPro’yu kullanmak, değişkenler arasındaki anlamlı ilişkileri ortaya çıkarmak için güçlü bir yol sağlar. QuestionPro’nun sezgisel arayüzünü, gelişmiş analitik araçlarını ve kapsamlı raporlama özelliklerini keşfederek, korelasyon analizini verimli bir şekilde gerçekleştirebilir ve verilerinizden değerli bilgiler elde edebilirsiniz. Daha fazla bilgi için QuestionPro ile bugün iletişime geçin!







