Regresyon analizi, bağımlı değişken ile bir dizi bağımsız açıklayıcı değişken arasındaki ilişkiyi araştırmak veya tahmin etmek için belki de en yaygın kullanılan istatistiksel tekniktir.
Ayrıca, çok sayıda değişkeni modellemek ve analiz etmek için nitel bir araştırma yönteminde kullanılan çeşitli veri analizi teknikleri için genel bir terim olarak kullanılır. Regresyon yönteminde, bağımlı değişken bir tahmin edici veya açıklayıcı unsurdur ve bağımlı değişken sonuç veya belirli bir sorguya verilen yanıttır.
Regresyon Analizi: Tanım
Regresyon analizi genellikle verileri modellemek veya analiz etmek için kullanılır. Anket analistlerinin çoğu bu yöntemi değişkenler arasındaki ilişkiyi anlamak için kullanmaktadır ve bu da kesin sonucu tahmin etmek için kullanılabilir.
Örneğin – Bir meşrubat şirketinin üretim birimini daha yeni bir yere genişletmek istediğini varsayalım. İlerlemeden önce; şirket, gelir yaratma modelini ve bunu etkileyebilecek çeşitli faktörleri analiz etmek istiyor. Bu nedenle, şirket bir
online anket
belirli bir anket ile.
Regresyon analizini kullandıktan sonra, şirketin anket sonuçlarını analiz etmesi ve elektrik ile gelir gibi farklı değişkenler arasındaki ilişkiyi anlaması kolaylaşır – burada gelir bağımlı değişkendir. Buna ek olarak, fiyatlandırma, işçi sayısı ve lojistik gibi farklı bağımsız değişkenlerin gelirle olan ilişkisinin anlaşılması, şirketin çeşitli faktörlerin şirketin satışları ve kârı üzerindeki etkisini tahmin etmesine yardımcı olur.
Anket araştırmacıları bu tekniği genellikle ilgilenilen farklı değişkenler arasındaki korelasyonu incelemek ve bulmak için kullanırlar. Şunları sağlar Farklı bağımsız değişkenlerin bağımlı değişken üzerindeki etkisini ölçmek için bir fırsat. Genel olarak regresyon analizi, çok sayıda bağımsız değişkeni tablolar halinde düzenlemek ve bağımlı değişken üzerindeki etkisini test etmek veya hesaplamak için anket araştırmacılarının ek çabalarından tasarruf sağlayan bir tekniktir. Yeni ürünleri değerlendirmek için farklı türde analitik yöntemler yaygın olarak kullanılmaktadır.
i̇ş fi̇ki̇rleri̇
ve bilinçli kararlar vermelerini sağlar.
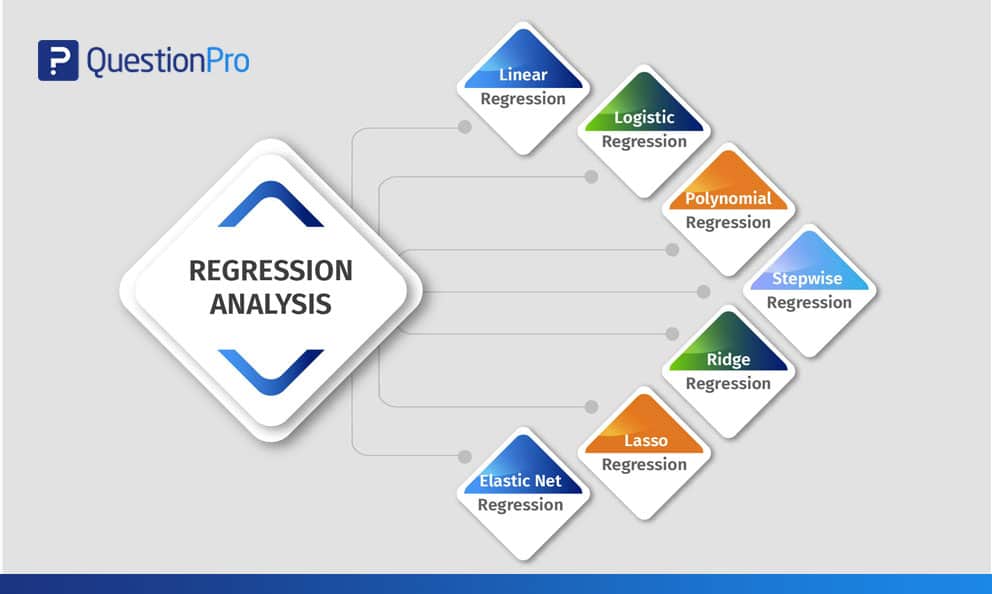
Regresyon Analizi Türleri
Araştırmacılar genellikle ilk olarak doğrusal ve lojistik regresyonu öğrenerek işe başlarlar. Bu iki yöntemin yaygın olarak bilinmesi ve uygulama kolaylığı nedeniyle, birçok analist sadece iki tür model olduğunu düşünmektedir. Her modelin kendi uzmanlık alanı ve belirli koşullar sağlandığında gerçekleştirme yeteneği vardır. Bu blog, çeşitli formatlardaki sayısız veriyi yorumlamak için kullanılabilecek yaygın olarak kullanılan yedi tür regresyon analizi yöntemini açıklamaktadır.
Doğrusal Regresyon Analizi
Tahmine dayalı modellemeyi öğrenirken insanlar tarafından seçilen ilk seçkin regresyon analizi yöntemlerinden biri olduğu için en yaygın bilinen modelleme tekniklerinden biridir. Burada, bağımlı değişken süreklidir ve bağımsız değişken daha çok süreklidir veya doğrusal bir regresyon çizgisi ile ayrıktır.
Çoklu doğrusal regresyonda birden fazla bağımsız değişken olduğunu, basit doğrusal regresyonda ise yalnızca bir bağımsız değişken olduğunu lütfen unutmayın. Bu nedenle, doğrusal regresyon yalnızca bağımsız ve bağımlı değişken arasında doğrusal bir ilişki olduğunda kullanılmalıdır
Örnek: Bir işletme, pazarlama kampanyalarının, fiyatlandırmanın ve promosyonların bir ürünün satışları üzerindeki etkinliğini ölçmek için doğrusal regresyonu kullanabilir. Diyelim ki spor malzemeleri satan bir şirket, ürünlerinin pazarlanması ve markalaşması için yatırdığı fonların kendilerine önemli bir getiri sağlayıp sağlamadığını anlamak istiyor. Doğrusal regresyon, sonuçları yorumlamak için en iyi istatistiksel yöntemdir. Doğrusal regresyonun en iyi yanı, her bir pazarlama ve markalaşma faaliyetinin belirsiz etkisini analiz etmeye yardımcı olurken, aynı zamanda bileşenin satışları düzenleme potansiyelini kontrol etmesidir. Eğer şirket aynı anda iki ya da daha fazla reklam kampanyası yürütüyorsa, örneğin biri televizyonda, ikisi radyoda, o zaman doğrusal regresyon hem bağımsız hem de bu reklamların birlikte yürütülmesinin birleşik etkisini kolayca analiz edebilir.
Lojistik Regresyon Analizi
Lojistik regresyon, genellikle aşağıdaki durumların olasılığını belirlemek için kullanılır
olay=Başarı
ve
olay=Başarısızlık
. Bağımlı değişken 0/1, Doğru/Yanlış, Evet/Hayır gibi ikili olduğunda lojistik regresyon kullanılır. Bu nedenle, lojistik regresyonun aşağıdaki iki durumu analiz etmek için kullanıldığı söylenebilir
kapalı uçlu sorular
veya bir ankette sayısal yanıt gerektiren sorular.
Lojistik regresyonun, doğrusal regresyon gibi bağımlı ve bağımsız değişken arasında doğrusal bir ilişkiye ihtiyaç duymadığını lütfen unutmayın. Lojistik regresyon, olasılık oranını tahmin etmek için doğrusal olmayan bir log dönüşümü uygular; bu nedenle, bir bağımlı ve bir bağımsız değişken arasındaki çeşitli ilişki türlerini kolayca ele alır.
Örnek: Lojistik regresyon, kategorik verileri analiz etmek için, özellikle de iş veri modellemesinde ikili yanıt verileri için yaygın olarak kullanılmaktadır. Lojistik regresyon daha çok bağımlı değişken kategorik olduğunda, örneğin bir kişi tarafından yapılan sağlık iddiasının gerçek(1) mi yoksa sahte mi olduğunu tahmin etmek, tümörün kötü huylu(1) olup olmadığını anlamak için kullanılır. İşletmeler, belirli bir demografik gruptaki tüketicilerin ürünlerini satın alıp almayacaklarını veya yaş, gelir, cinsiyet, ırk, ikamet durumu, önceki satın alma vb. temelinde rakiplerden satın alıp almayacaklarını tahmin etmek için lojistik regresyonu kullanır.
Polinom Regresyon Analizi
Polinom regresyon genellikle eğrisel verileri analiz etmek için kullanılır ve bu, bağımsız bir değişkenin gücü 1’den fazla olduğunda gerçekleşir. Bu regresyon analizi yönteminde, en iyi uyum çizgisi hiçbir zaman bir ‘düz çizgi’ değil, her zaman veri noktalarına uyan bir ‘eğri çizgi’dir.
Lütfen polinom regresyonun, değişkenlerin çok azının üslü, çok azının ise üssüz olduğu durumlarda kullanılmasının daha iyi olduğunu unutmayın. Ayrıca, doğrusal olarak ayrılamayan verileri modelleyebilir ve her değişken için tam üssü seçme özgürlüğü sunar ve bu da mevcut modelleme özellikleri üzerinde tam kontrol sağlar.
Örnek: Polinom regresyonu, yanıt yüzeyi analizi ile birleştirildiğinde, çok kaynaklı geri bildirim araştırmalarında yaygın olarak kullanılan sofistike bir istatistiksel yaklaşım olarak kabul edilir. Polinom regresyonu çoğunlukla bağımlı ve bağımsız değişken arasındaki ilişkinin eğrisel olduğu finans ve sigortacılıkla ilgili sektörlerde kullanılır. Bir kişinin belirli bir miktar parayı kazanmak için ne kadar zaman gerektiğini belirleyerek gider planlaması yapmak istediğini varsayalım. Polinom regresyonu, gelirini dikkate alarak ve harcamalarını tahmin ederek, belirli bir miktar kazanmak için çalışması gereken kesin süreyi kolayca belirleyebilir.
Adımsal Regresyon Analizi
Bu, tahmin edilen katsayılarının t-istatistiklerine bağlı olan değişkenlerin eklenmesi veya çıkarılması yoluyla istatistiksel bir modelin oluşturulduğu yarı otomatik bir süreçtir. Doğru kullanıldığında, kademeli regresyon size herhangi bir yöntemden daha güçlü verileri parmaklarınızın ucunda sunacaktır. Çok sayıda bağımsız değişkenle çalıştığınızda iyi sonuç verir. Sadece değişkenleri rastgele dürtmek suretiyle analiz modeline ince ayar yapar. Adımsal regresyon analizinin birden fazla bağımsız değişken olduğunda kullanılması tavsiye edilir, burada bağımsız değişkenlerin seçimi insan müdahalesi olmadan otomatik olarak yapılır.
Aşamalı regresyon modellemesinde, değişkenin açıklayıcı değişkenler kümesine eklendiğini veya çıkarıldığını lütfen unutmayın. Eklenen veya çıkarılan değişkenler kümesi, tahmin edilen katsayının test istatistiklerine bağlı olarak seçilir.
Örnek: Diyelim ki yaş, kilo, vücut yüzey alanı, hipertansiyon süresi, bazal nabız ve stres indeksi gibi kan basıncı üzerindeki etkisini analiz etmek istediğiniz bir dizi bağımsız değişkeniniz var. Adımsal regresyonda, bağımsız değişkenin en iyi alt kümesi otomatik olarak seçilir, ya ilerlemek için hiçbir değişken seçmeyerek başlar (her seferinde bir değişken ekler) ya da modeldeki tüm değişkenlerle başlar ve geriye doğru ilerler (her seferinde bir değişkeni kaldırır). Böylece, regresyon analizini kullanarak, her bir değişkenin veya bir grup değişkenin kan basıncı üzerindeki etkisini hesaplayabilirsiniz.
Ridge Regresyon Analizi
Ridge regresyonu, çoklu doğrusal bağlantı verilerini (bağımsız değişkenlerin yüksek oranda ilişkili olduğu veriler) analiz etmek için kullanılan sıradan bir en küçük kare yöntemine dayanmaktadır. Doğrusal bağlantı, değişkenler arasında doğrusala yakın bir ilişki olarak açıklanabilir. Çoklu doğrusal bağlantı olduğunda, en küçük kareler tahminleri yansız olacaktır; ancak, aralarındaki fark daha büyükse, o zaman gerçek değerden uzak olabilir. Ancak ridge regresyonu, daha güvenilir tahminler sağlamak amacıyla regresyon tahminlerine bir dereceye kadar yanlılık ekleyerek standart hataları ortadan kaldırır.
Lütfen ridge regresyonu yoluyla elde edilen varsayımların en küçük kareli regresyona benzer olduğunu, tek farkın normallik olduğunu unutmayın. Katsayının değeri ridge regresyonunda daralmış olsa da, hiçbir zaman sıfıra ulaşmaz ve bu da değişkenlerin seçilemediğini gösterir.
Örnek: Diyelim ki yakınınızdaki bir etkinlikte canlı performans sergileyen iki gitarist için deli oluyorsunuz ve kimin daha iyi bir gitarist olduğunu öğrenmek için performanslarını izlemeye gidiyorsunuz. Ancak performans başladığında, her ikisinin de aynı anda siyah-mavi notalar çaldığını fark ediyorsunuz. Her ikisi de yüksek sesle ve hızlı çalarken aralarında ses üzerinde en büyük etkiye sahip olan en iyi gitaristi bulmak mümkün mü? Her ikisi de farklı notalar çaldığından, bunları ayırt etmek oldukça zordur, bu da çoklu doğrusallığın en iyi örneğidir ve bu da katsayıların standart hatalarını artırma eğilimindedir. Ridge regresyonu bu gibi durumlarda çoklu doğrusallığı ele alır ve sonuçları elde etmek için yanlılık veya daralma tahmini içerir.
Kement Regresyon Analizi
Kement (En Küçük Mutlak Küçültme ve Seçim Operatörü) sırt regresyonuna benzer; ancak sırt regresyonunda kullanılan kare önyargı yerine mutlak değer önyargısı kullanır. Bu yöntem, 1989 yılında geleneksel en küçük kareler tahminine alternatif olarak, verilerin çok sayıda bağımsız değişkene sahip olduğu durumlarda aşırı uyumla ilgili sorunların çoğunu ortadan kaldırmak amacıyla geliştirilmiştir. Lasso, değişkenleri seçme ve yumuşak bir eşikle birlikte düzenli hale getirme gibi her ikisini de gerçekleştirme yeteneğine sahiptir. Kement regresyonu uygulayarak, nicel bir yanıtı analiz ederken tahmin hatalarının en aza indirilebilmesi için bir tahminci alt kümesi türetmek daha kolay hale gelir.
Kement modelinde, daraltma sonrasında sıfır değerine ulaşan regresyon katsayısının modelden çıkarıldığını lütfen unutmayın. Aksine, sıfırdan büyük değere sahip regresyon katsayıları, açıklayıcı değişkenlerin nicel, kategorik veya her ikisi birden olabileceği yanıt değişkenleriyle güçlü bir şekilde ilişkilidir.
Örnek: Bir otomobil şirketinin ABD’deki otomobillerin ortalama yakıt tüketimine ilişkin bir araştırma analizi yapmak istediğini varsayalım. Örnekler için 32 otomobil modeli ve otomobil tasarımının 10 özelliğini seçtiler – Silindir sayısı, Deplasman, Brüt beygir gücü, Arka aks oranı, Ağırlık, ¼ mil süresi, v/s motor, şanzıman, vites sayısı ve karbüratör sayısı. Gördüğünüz gibi yanıt değişkeni mpg (galon başına mil) ile ağırlık, silindir sayısı ve beygir gücü gibi bazı değişkenler arasında son derece yüksek bir korelasyon vardır. Bu sorun, aşağıdaki yöntemlerden yararlanılarak analiz edilebilir
glmnet
paketini kullanarak ve özellik seçimi için lasso regresyonu kullanarak gerçekleştirilmiştir.
Elastik Ağ Regresyon Analizi
L1 ve L2 normu ile eğitilmiş ridge ve lasso regresyon modellerinin bir karışımıdır. Elastik ağ, güçlü korelasyon gösteren tahmin edicilerin modele birlikte girip çıkma eğiliminde olduğu bir gruplama etkisi yaratır. Tahmin edicilerin sayısı gözlem sayısından çok daha fazla olduğunda elastik ağ regresyon modelinin kullanılması önerilir.
Elastik net regresyon modelinin, lasso regresyon modeline bir seçenek olarak ortaya çıktığını lütfen unutmayın, çünkü lasso’nun değişken bölümü verilere çok fazla bağımlıydı ve bu da onu kararsız hale getiriyordu. Elastik ağ regresyonunu kullanarak istatistikçiler, her iki modelden de en iyi sonucu almak için ridge ve lasso regresyonunun cezalarını aşma yeteneğine sahip oldular.
Örnek: Lösemi (LEU) ile ilgili bir mikroarray veri setine erişimi olan bir klinik araştırma ekibi, lösemi türünü tahmin etmek için sunulan gen örneklerinin ifade düzeyine dayalı bir tanı kuralı oluşturmak istiyordu. Ellerindeki veri seti, çok sayıda gen ve az sayıda örnekten oluşuyordu. Bunun dışında, eğitim numunesi olarak kullanılmak üzere, bazıları tip 1 lösemi (akut lenfoblastik lösemi) ve bazıları tip 2 lösemi (akut miyeloid lösemi) ile enfekte olan belirli bir numune seti verildi. Eğitim verileri üzerinde model uydurma ve on kat CV ile ayarlama parametresi seçimi gerçekleştirilmiştir. Daha sonra, gerekli sonuçları elde etmek için test verileri üzerinde tahmin ortalama-kare hatalarını hesaplayarak bu yöntemlerin performansını karşılaştırdılar.
Pazar araştırmasında kullanım
Üç ana matrise odaklanan bir pazar araştırması anketi gerçekleştirilir;
Müşteri Memnuniyeti
, Müşteri Sadakati ve Müşteri Savunuculuğu. Unutmayın, bu matrisler bize müşteri sağlığı ve niyetleri hakkında bilgi verse de, durumu iyileştirmenin yollarını göstermez. Bu nedenle, tüketicilere memnuniyetsizliklerinin nedenini sormayı amaçlayan derinlemesine bir anket kesinlikle pratik bilgiler edinmenin bir yoludur.
Ancak, insanların genellikle motivasyonlarını veya motivasyonsuzluklarını ortaya koymakta veya memnuniyetlerini veya memnuniyetsizliklerini tanımlamakta zorlandıkları tespit edilmiştir. Buna ek olarak, insanlar her zaman fiyat, ambalaj vb. gibi bazı rasyonel faktörlere gereğinden fazla önem vermektedir. Genel olarak, pazar araştırmasında öngörücü bir analitik ve tahmin aracı olarak işlev görür.
Bir tahmin aracı olarak kullanıldığında regresyon analizi, dış pazar verilerini dikkate alarak bir kuruluşun satış rakamlarını belirlemek için kullanılabilir. Çok uluslu bir şirket, GSYİH (Gayri Safi Yurtiçi Hasıla), TÜFE (Tüketici Fiyat Endeksi) ve diğer benzer faktörler gibi çeşitli faktörlerin gelir yaratma modeli üzerindeki etkisini anlamak için bir pazar araştırması yürütür. Açıkçası, gelecek çeyreklerde ve hatta gelecek yıllarda elde edilecek geçici bir geliri tahmin etmek için tahmini pazarlama göstergeleri dikkate alınarak regresyon analizi kullanılmıştır. Ancak, gelecekte daha ileri gidildikçe veriler daha güvenilmez hale gelecek ve geniş bir hata payı bırakacaktır.
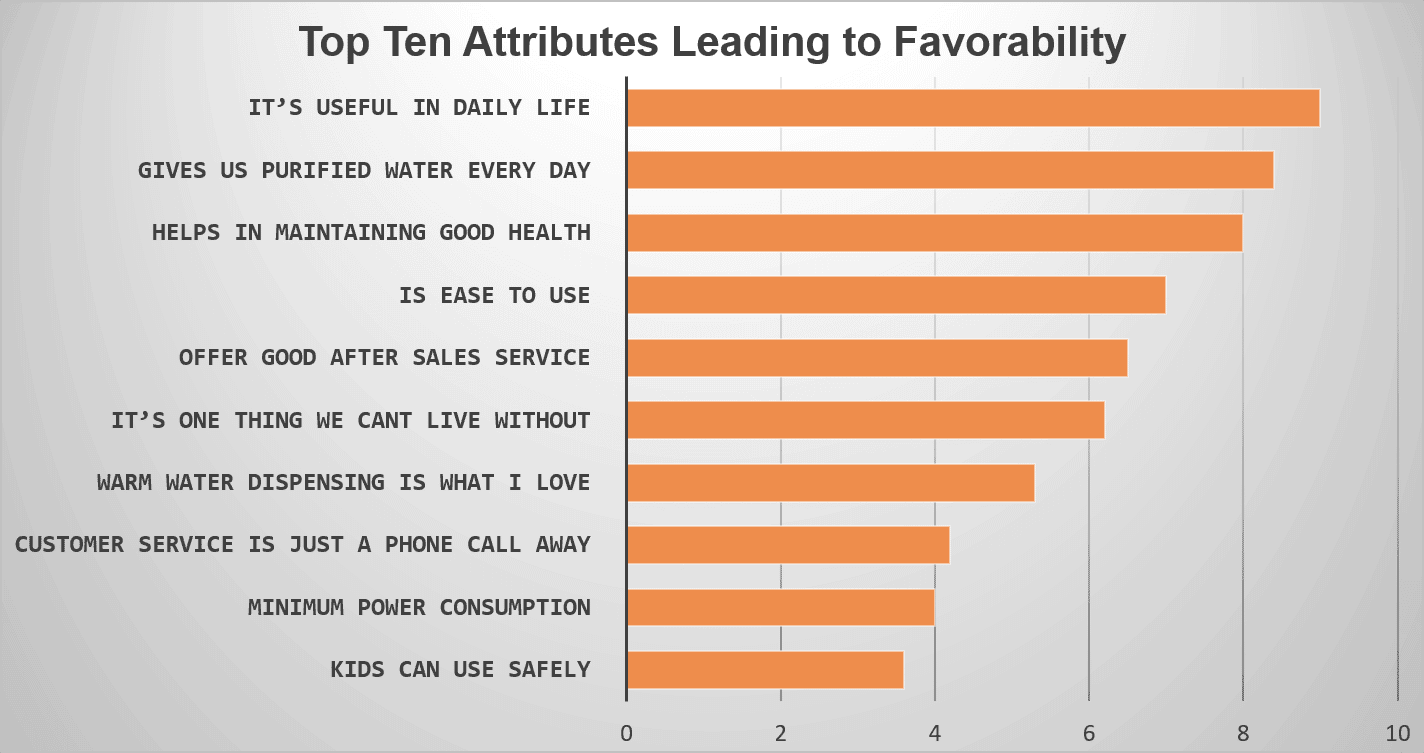
Örnek: Bir su arıtma cihazı şirketi, marka tercih edilirliğine yol açan faktörleri anlamak istedi. Anket, mevcut ve potansiyel müşterilere ulaşmak için en iyi araçtı. Büyük ölçekli bir tüketici anketi planlanmış ve en iyi anket aracı kullanılarak gizli bir anket hazırlanmıştır. Ankette marka, tercih edilirlik, memnuniyet ve olası memnuniyetsizlikle ilgili bir dizi soru etkin bir şekilde sorulmuştur. Ankete optimum yanıtlar alındıktan sonra, marka tercih edilirliğini yönlendiren ilk on faktörü daraltmak için regresyon analizi kullanılmıştır. Türetilen (aşağıdaki resimde belirtilen) on özelliğin tümü, şu veya bu şekilde, söz konusu su arıtma cihazı markasının tercih edilirliğini etkilemedeki önemlerini vurgulamıştır.
Regresyon analizi anketlerden nasıl içgörü elde eder?
Excel veya SPSS kullanarak bir regresyon analizi yapmak kolaydır, ancak bunu yaparken dört sayının verileri yorumlamadaki önemi anlaşılmalıdır.
Dört sayıdan ilk ikisi doğrudan regresyon modelinin kendisiyle ilgilidir.
F-Değeri: Anket modelinin istatistiksel anlamlılığının ölçülmesine yardımcı olur. Unutmayın, 0,05’ten önemli ölçüde küçük bir F-Değeri daha anlamlı olarak kabul edilir. 0,05’ten küçük F-Değeri, anket analizi çıktısının tesadüfi olmamasını sağlar.
- R-Kare: Bağımsız değişkenin bağımlı değişken tarafından hareket miktarını açıklamaya çalıştığı değerdir. R-Squared değerinin 0,7 olduğunu düşünürsek, bu bağımlı değişkenin hareketinin %70’inin test edilen bağımsız değişken tarafından açıklanabileceği anlamına gelir. Bu, elde edeceğimiz anket analizi çıktısının doğası gereği son derece öngörücü olduğu ve doğru kabul edilebileceği anlamına gelir.
Diğer iki sayı, regresyon analizi yorumlanırken bağımsız değişkenlerin her biriyle ilgilidir.
- P-Değeri: Tıpkı F-Değeri gibi, P-Değeri de büyük istatistiksel öneme sahiptir. Ayrıca, burada bağımsız değişkenin etkisinin ne kadar ilgili ve istatistiksel olarak anlamlı olduğunu gösterir. Bir kez daha, 0,05’ten küçük bir değer arıyoruz.
- Dördüncü sayı, değişkenlerin etkisi ölçüldükten sonra elde edilen katsayı ile ilgilidir. Örneğin, ‘diğer tüm bağımsız değişkenler aynı değerde sabitken bağımsız değişkenler (dikkate aldığımız) bir arttığında bağımlı değişkenin ne kadar artması beklendiğini’ söyleyen bir katsayı elde etmek için birden fazla bağımsız değişkeni test ederiz. Birkaç durumda, basit katsayının yerini, her bir bağımsız değişkenin bağımlı değişkeni hareket ettirmek veya bir değişiklik meydana getirmek için yaptığı katkıyı gösteren standartlaştırılmış bir katsayı alır.
Çevrimiçi bir ankette regresyon analizi kullanmanın avantajları
Tahmine dayalı analitiklere erişim sağlayın:
Bir araştırmanın sonucunu anlamak için regresyon analizini kullanmayı biliyor musunuz?
i̇ş anketi̇
gelecekteki fırsatları ve riskleri ortaya çıkarma gücüne sahip olmak gibi mi?
Örneğin, belirli bir televizyon reklamı aralığını gördükten sonra, o aralık için maksimum teklifi tahmin etmek için bu verileri kullanarak işletmelerin tam sayısını tahmin edebiliriz. Bir bütün olarak finans ve sigorta sektörü, daha doğru planlama ve karar verme için eğilimleri ve fırsatları belirlemek üzere anket verilerinin regresyon analizine büyük ölçüde bağlıdır.
Operasyonel verimliliği artırın:
İşletmelerin iş süreçlerini optimize etmek için regresyon analizini kullandığını biliyor musunuz?
Örneğin, işletmeler yeni bir ürün grubunu piyasaya sürmeden önce
tüketi̇ci̇ anketi̇
çeşitli faktörlerin o ürünün üretimi, paketlenmesi, dağıtımı ve tüketimi üzerindeki etkisini daha iyi anlamak amacıyla. Veriye dayalı bir öngörü, tahmin, varsayım ve iç politikanın karar alma sürecinden çıkarılmasına yardımcı olur. Operasyonel verimliliği ve gelirleri etkileyen alanların daha iyi anlaşılması, daha iyi iş optimizasyonuna yol açar.
Karar verme için niceliksel destek:
İş anketleri Günümüzde finans, gelir, operasyon, satın alma vb. ile ilgili çok sayıda veri üretilmektedir ve işletme sahipleri bilinçli iş kararları almak için çeşitli veri analizi modellerine büyük ölçüde bağımlıdır.
Örneğin regresyon analizi, işletmelerin bilinçli stratejik işgücü kararları almasına yardımcı olur. Çalışan Bağlılığı Anketi, Çalışan Memnuniyeti Anketi, İşveren İyileştirme Anketi, Çalışan Çıkış Anketi gibi çalışan anketlerinin yapılması ve sonuçlarının yorumlanması, çalışan ve işletme arasındaki ilişkinin anlaşılmasını artırır. Ayrıca, kurumun çalışma kültürünü, çalışma ortamını ve verimliliğini etkileme kapasitesine sahip belirli konular hakkında adil bir fikir edinilmesine de yardımcı olur. Ayrıca, akıllı iş odaklı yorumlamalar yoluyla, daha bilinçli bir karar vermek için devasa ham veri yığınını eyleme dönüştürülebilir bilgilere indirger.
Sezgiler nedeniyle meydana gelen hataları önleyin:
Bilerek
regresyon analizi nasıl kullanılır
Anket sonuçlarını yorumlamak için, bilinçli kararlar almak için yönetime kolayca gerçeklere dayalı destek sağlanabilir. Ancak, bunun aynı zamanda yargıdaki hataları dışarıda tutmaya da yardımcı olduğunu biliyor musunuz?
Örneğin, bir alışveriş merkezi yöneticisi, alışveriş merkezinin kapanış saatini uzatırsa, bunun daha fazla satışla sonuçlanacağını düşünür. Regresyon analizi, artan satışlar nedeniyle artan gelirin, daha uzun çalışma saatlerinden kaynaklanan artan işletme giderlerini desteklemek için yeterli olmayacağını öngörerek bu inanışla çelişmektedir.







