Spearman korelasyon katsayısı: Tanım
Spearman’ın sıra korelasyon katsayısı veya Spearman korelasyon katsayısı, sıra korelasyonunun parametrik olmayan bir ölçüsüdür (iki değişken arasındaki sıralamanın istatistiksel bağımlılığı).
Charles Spearman’ın adıyla anılan bu terim genellikle Yunanca ‘ρ’ (rho) harfiyle gösterilir ve öncelikle veri analizi için kullanılır.
İki sıralı değişken arasındaki ilişkinin gücünü ve yönünü ölçer. Ancak Spearman korelasyon katsayısından bahsetmeden önce Pearson korelasyonunu anlamak önemlidir. Pearson korelasyonu, eşleştirilmiş veriler arasındaki doğrusal ilişkinin gücünün istatistiksel bir ölçüsüdür.
Sıralama değişkeninin hesaplanması ve anlamlılık testi için aşağıdaki veri varsayımının doğru olması gerekmektedir:
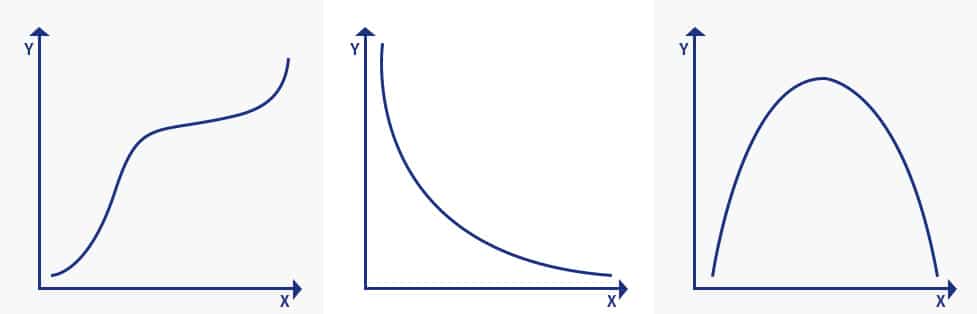
Verileriniz yukarıdaki varsayımları karşılamıyorsa, Spearman Katsayısına ihtiyacınız olacaktır. Spearman korelasyon katsayısını anlamak için monotonik fonksiyonun ne olduğunu bilmek gerekir. Monoton bir fonksiyon, bağımsız değişken arttıkça ya hiç azalmayan ya da hiç artmayan bir fonksiyondur. Monotonik bir fonksiyon aşağıdaki resim kullanılarak açıklanabilir:
Görsel, monotonik fonksiyonla ilgili üç kavramı açıklamaktadır:
- Monoton olarak artan: ‘x’ değişkeni arttığında ve ‘y’ değişkeni asla azalmadığında.
- Monoton olarak azalan: ‘x’ değişkeni artarken ‘y’ değişkeni hiç artmadığında
- Monotonik değil: ‘x’ değişkeni arttığında ve ‘y’ değişkeni bazen arttığında ve bazen azaldığında.
Monotonik ilişki, Pearson katsayısında kullanılan doğrusal ilişkiye kıyasla daha az kısıtlayıcıdır. Monotonluk Spearman korelasyon katsayısı için nihai gereklilik olmasa da, değişkenler arasındaki ilişkinin monoton olmadığı zaten biliniyorsa, monotonik bir ilişkinin gücünü ve yönünü gerçekten belirlemeden Spearman korelasyonunu takip etmek anlamlı olmayacaktır.
Daha fazla bilgi edinin: Örneklerle Çim Analizi
Spearman korelasyon katsayısı: Formül ve Örnekle Hesaplama
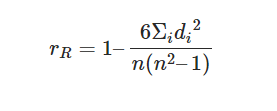
n= iki değişkene ait veri noktası sayısı
di=“ith” elemanının rütbelerindeki fark
Spearman Katsayısı, ⍴, +1 ile -1 arasında bir değer alabilir,
- 1’lik bir ⍴ değeri, mükemmel bir rütbe ilişkisi anlamına gelir
- ⍴ değerinin 0 olması rütbeler arasında bir ilişki olmadığı anlamına gelir
- ⍴ değerinin -1 olması, sıralamalar arasında mükemmel bir negatif ilişki olduğu anlamına gelir.
⍴ değeri 0’a ne kadar yakınsa, iki rütbe arasındaki ilişki o kadar zayıftır.
Spearman’ın Sıralama Korelasyon Katsayısı ile devam etmeden önce verileri sıralayabilmeliyiz. Bir değişken arttığında diğer değişkenin monoton bir ilişki izleyip izlemediğini gözlemlemek önemlidir.
Her seviyede, iki değişkenin değerlerini karşılaştırmanız gerekecektir. Hesaplamalar şu şekilde yapılır:
9 öğrencinin Tarih ve Coğrafya derslerinden aldıkları puanlar aşağıdaki tabloda belirtilmiştir.
Adım 1- Elde edilen verilerin bir tablosunu oluşturun.
Adım 2- İki veri setini sıralayarak başlayın. Veri sıralaması, sütundaki en büyük sayıya “1”, ikinci en büyük sayıya “2” ve benzeri bir sıralama atanarak elde edilebilir. En küçük değer genellikle en düşük sıralamayı alacaktır. Bu işlem her iki ölçüm seti için de yapılmalıdır.
Adım 3- Veri setinize üçüncü bir d sütunu ekleyin, d burada sıralamalar arasındaki farkı ifade eder. Örneğin, ilk öğrencinin fizik sıralaması 3 ve matematik sıralaması 5 ise, sıralamadaki fark 3’tür. Dördüncü sütunda d değerlerinin karesini alın.
| Tarih | Rütbe | Coğrafya | Rütbe | d | d kare |
| 35 | 3 | 30 | 5 | 2 | 4 |
| 23 | 5 | 33 | 3 | 2 | 4 |
| 47 | 1 | 45 | 2 | 1 | 1 |
| 17 | 6 | 23 | 6 | 0 | 0 |
| 10 | 7 | 8 | 8 | 1 | 1 |
| 43 | 2 | 49 | 1 | 1 | 1 |
| 9 | 8 | 12 | 7 | 1 | 1 |
| 6 | 9 | 4 | 9 | 0 | 0 |
| 28 | 4 | 31 | 4 | 0 | 0 |
| 12 |
Adım 4- Tüm d kare değerlerinizi toplayın, yani 12 (∑d kare)
Adım 5- Bu değerleri formüle ekleyin
=1-(6*12)/(9(81-1))
=1-72/720
=1-01
=0.9
Bu veriler için Spearman’ın Sıralama Korelasyonu 0,9’dur ve yukarıda belirtildiği gibi ⍴ değeri +1’e yakınsa mükemmel bir sıralama ilişkisine sahiptirler.
Daha fazla bilgi edinin: Konjoint Analizi – Tanım, Türler, Örnek, Algoritma ve Model
QuestionPro ile korelasyon katsayısı nasıl yapılır
Bu bölümde, anketiniz için Spearman’ın Sıra Korelasyon Katsayısını nasıl çalıştırabileceğinizi öğreneceksiniz.
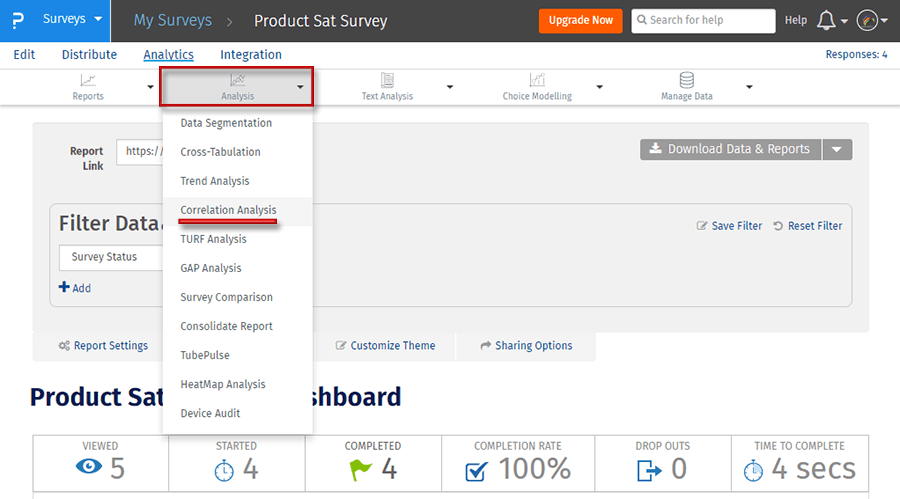
Adım 1: Anketlerim → Anket Seç→Analitik bölümüne gidin
Adım 2: Analiz altında Korelasyonel Analiz üzerine tıklayın
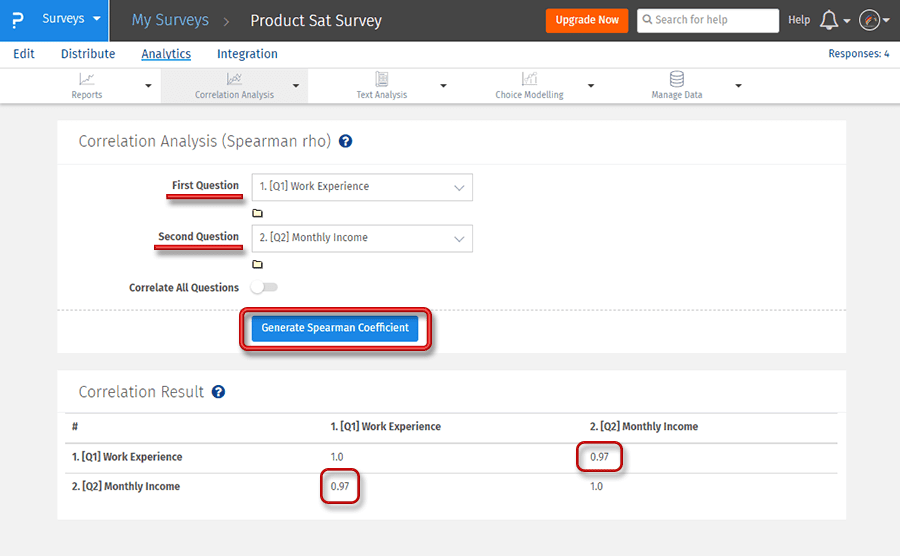
Adım 3: Ayrıntılı bir rapor almak için Spearman Katsayısı Oluştur düğmesine tıklayın
Yukarıdaki örnekte, iki değişken olan İş deneyimi ve Aylık gelir arasındaki ilişkiyi bulmak için Spearman korelasyon katsayısı kullanılmıştır. Genel bir kanıya göre, aylık gelir iş tecrübesi ile birlikte artmalıdır, bu da iki değişken arasında pozitif bir ilişki olması gerektiği anlamına gelir ki bu da 0.97 olan rs değeri ile kanıtlanmıştır
Daha fazla bilgi edinin: GAP Analizi – Tanım, Yöntem ve Örnekli Şablon