ピアソン相関係数を用いて線形関係を定量化するのが通常のやり方です。2つの変数の間の接続の強さと方向を示すために、それは-1から1の間の値を取ります。
投資家の分散に役立ちます。株式-債券、株式-コモディティ、債券-不動産など、資産のペア間の過去のリターンの散布図から計算することにより、投資家がリスク-リターンのポートフォリオを構築するのに役立ちます。
そこで、ピアソン相関係数について学び、それを使って関連する2つの変数の関係を測定する方法を学びます。
ピアソン相関係数とは?
ピアソン相関係数(Pearson correlation coefficient)またはピアソンの相関係数(Pearson’s correlation coefficient)またはピアソンのr(Pearson’s r)は、統計学では、2つの変数間の関係の強さの測定、およびそれらの互いの関連性と定義されます。
簡単に言うと、ピアソンの相関係数は変数が変化したときの、もう1つの変数の変化の効果を計算します。
例: ある年齢まで(ほとんどの場合)、子供の身長は年齢が上がるにつれて伸び続けます。もちろん、その子の成長は遺伝子、場所、食事、ライフスタイルなど様々な要因に依存します。
このアプローチは共分散に基づいており、したがって、2つの変数の間の関係を測定するための最良の方法です。
ピアソン相関係数のテストとは?
ピアソン係数相関は、統計的有意性が高いです。これは2つの変数の間の関係に注目します。これは、2つの変数のデータを通して線を引き、それらの関係を示そうとします。変数の関係は、ヘルプピアソン相関係数電卓で測定されます。この線形関係は、正または負のことができます。
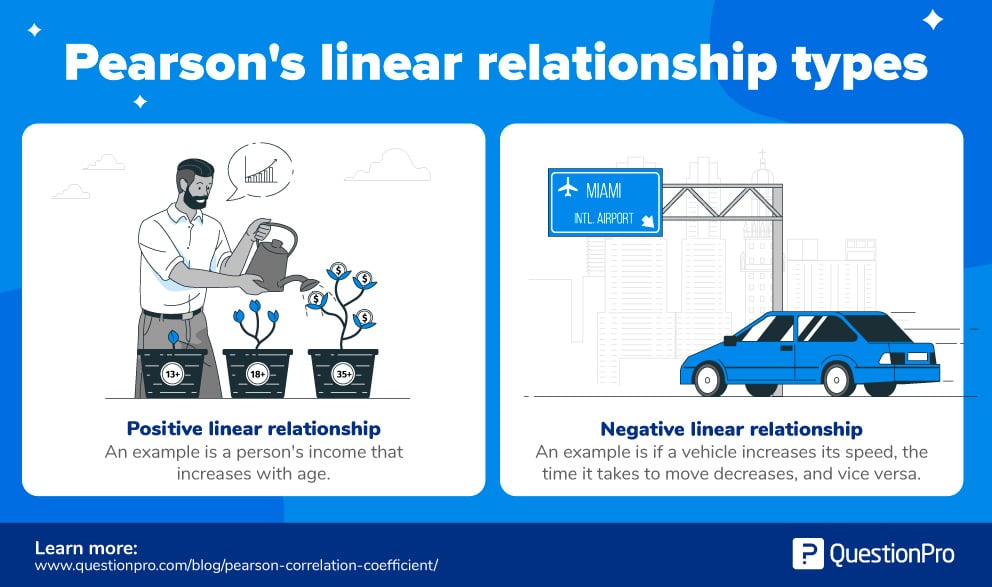
例:
- 正の線形関係: ほとんどの場合、普遍的に、人の収入は年齢が増加するにつれて増加します。
- 負の線形関係:車速を上げると走行時間が短くなり、逆に車速を下げると走行時間が長くなる。
上記の例から、ピアソン相関係数rは、与えられたサンプルサイズから関係の強さと方向性の2つを見つけ出そうとしていることがわかります。
ピアソン相関係数の公式と計算
相関係数の式は、変数間の関係を見つけます。それは-1から1の間の値を返します。2つの変数の強さを測定するために、以下のピアソン係数相関計算機を使用してください。
ピアソン相関係数の式:
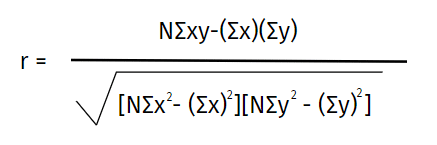
ここでは:
N = スコアのペアの数
Σxy = ペアのスコアの積の合計
Σx = xのスコアの合計
Σy = yスコアの合計
Σx2 = xスコアの2乗和
Σy2 = yスコアの2乗和
計算方法
以下は、ピアソンの相関係数を計算するためのステップ・バイ・ステップのガイドです:
ステップ1:相関係数表を作成します。
両方の変数を含むデータ表を作成します。これらの変数に ‘x’ と ‘y’ のラベルを付けます。(xy)、(x^2)、(y^2)の3つの列を追加します。この簡単なデータ・チャートを参照してください。

ステップ2:基本的な掛け算を使って表を完成させます。

ステップ3:すべての列を下から上に足し算します。
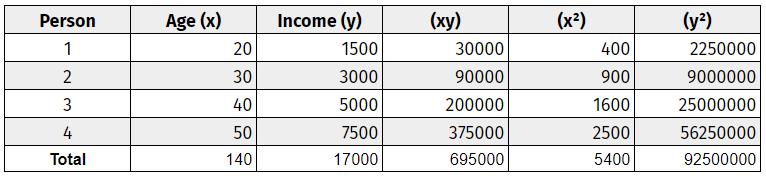
ステップ4:相関式を使用して値を差し込みます。
結果が負の場合、2つの変数の間に負の相関関係があります。結果が正なら、変数間に正の相関関係があります。結果は、線形関係の強さ、すなわち、強い正の関係、強い負の関係、中程度の正の関係なども定義できます。
ピアソン積率相関係数の強さの決定
ピアソン積率相関係数、または単にピアソン相関係数、またはピアソン係数相関 r は、2つの変数の間の線形関係の強さを決定します。
2つの変数の間の関連が強ければ強いほど、答えは1または-1に近づきます。1または-1の値を得ることは、すべてのデータ・ポイントが「ベスト・フィット」の直線上にプロットされることを意味します。それは、いずれかの変数の係数の変化が、他の変数との相関を弱めないことを意味します。答えが0に近いほど、変数のばらつきが大きいことを意味します。
ピアソン相関係数の解釈方法
下記は、ピアソン係数相関の解釈のためのガイドラインです: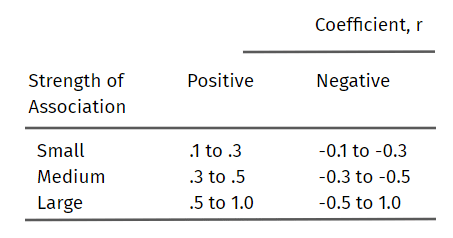
変数の関連性の強さは、測定するものと標本サイズに依存することに注意してください。
グラフ上で、変数の間の関係に気づき、計算する前に仮定を立てることができます。散布図が直線に近ければ、変数間の強い関係を示します。
散布図が線に近ければ近いほど、変数間の関係が強いことを示します。散布図が線から遠ざかれば遠ざかるほど、関係は弱くなります。散布図がグラフ上にランダム化されているため、線がx軸にほぼ平行であれば、2つの変数の間には相関がないと考えてよいでしょう。
強さと方向という用語は何を意味しますか?
「強さ」と「方向」という用語には統計的な意味があります。この2つの言葉をわかりやすく説明します:
- 強さ: 強さは、2つの変数の間の関係相関を意味します。それは、もう一方の変数の変化によって、一方の変数がどれだけ一貫して変化するかを意味します。1または-1に近い値は、強い関係を示します。これらの値は、データポイントが線上にあるか、線に非常に近い場合に達成されます。
データ点が遠ざかれば遠ざかるほど、直線関係の強さは弱くなります。データ点が散らばっていて、直線を引く現実的な方法がない場合、直線関係の強さは最も弱くなります。 - 方向:直線の方向は、変数間の正の線形関係または負の線形関係を示します。直線が上向きの傾きを持つ場合、変数は正の関係を持ちます。
これは、1つの変数の値の増加が、もう1つの変数の値の増加につながることを意味します。負の相関は、下向きの傾きを示します。これは、1つの変数の量の増加が、もう1つの変数の値の減少につながることを意味します。
ピアソン相関係数の例
相関係数の表を解釈するために、いくつかの視覚的な例を見てみましょう:
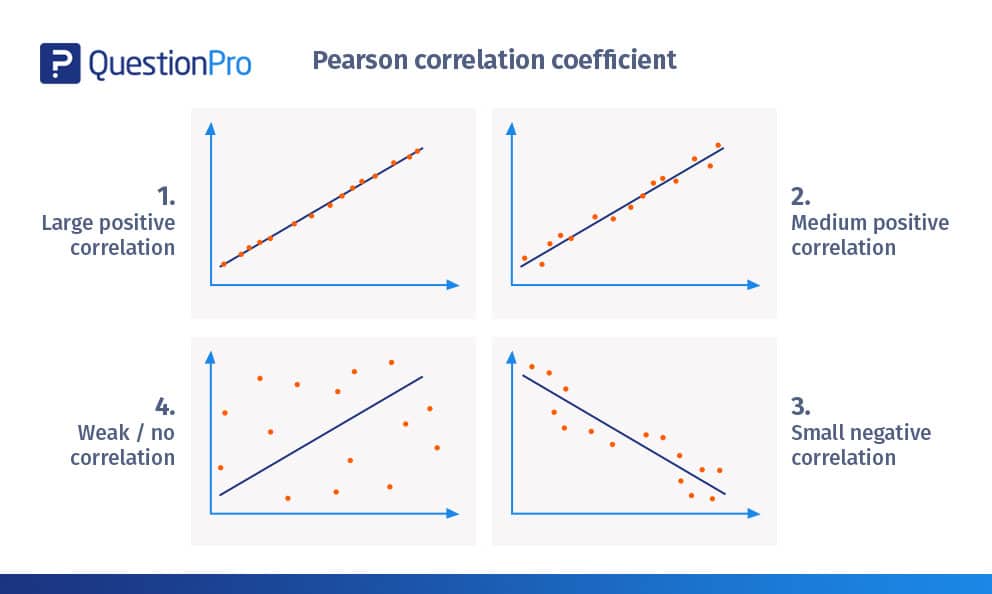
大きな正の相関
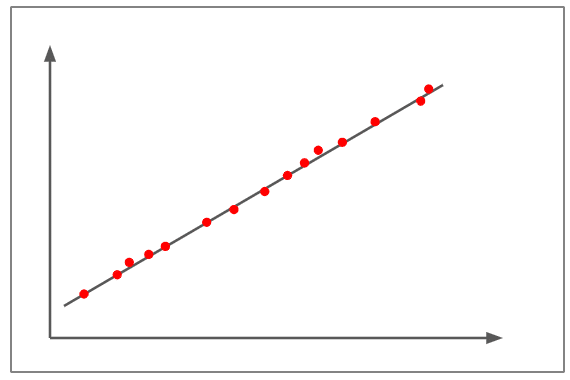
- 上の図は、ほぼ+1の相関を描いています。
- 散布図はほぼ直線にプロットされています。
- 傾きは正で、これは1つの変数が増加すると、もう1つの変数も増加することを意味し、正の直線を示します。
- これは、一方の変数の変化がもう一方の変数の変化に正比例することを示します。
- 大きな正の相関の例は、 – 子供の成長とともに、彼らの服や靴のサイズも大きくなります。
中程度の正の相関
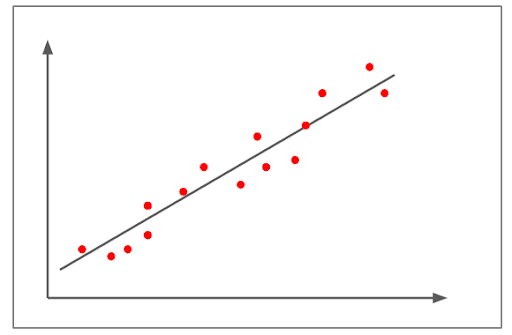
- 上の図は、正の相関を示しています。
- 相関は+0.8以上ですが、1+以下です。
- かなり強い直線的な上昇パターンを示しています。
- 中程度の正の相関の例としては、 – 自動車の数が増加するにつれて、燃料変数の需要も増加します。
小さな負の相関
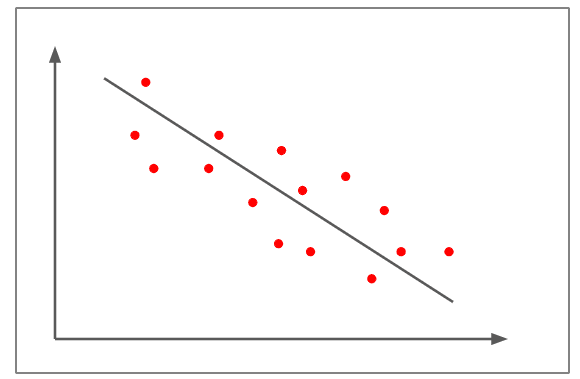
- 上の図では、散布図は先の例と比較して直線に近くありません。
- 約-0.5の負の直線相関を示しています。
- 傾きが負なので、一方の変数の変化は、もう一方の変数の変化に反比例します。
- 小さな負の相関の例としては、「食べれば食べるほど、お腹が空かなくなる」などがあります。
弱い/相関なし
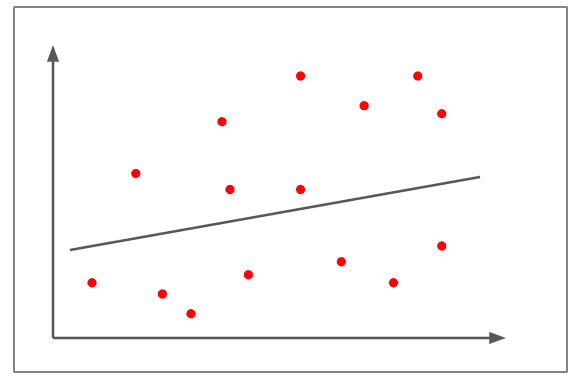
- 散布図が直線から離れています。
- 実際に線を引くのは難しい。
- 相関は約+0.15
- 一方の変数の変化が他方の変数に正比例、反比例しているとは判断できません。
- 相関が弱い/相関がない例としては、「燃料価格が上昇すると、ペットを飼う人が減る」などがあります。
結論
ピアソン相関係数は、調査を通して関心のある2つの変数のデータを収集することによって決定することができます。これを使って、2つの変数間の相関が正か負か、またどの程度強いかを知ることができます。
QuestionPro Research Suiteは、調査を活用し、インサイトを変換するためのツール群で、ピアソン相関係数分析のためのデータ収集に使用できます。QuestionProから調査データをエクスポートし、スプレッドシートや統計アプリケーションにインポートした後、相関分析を行うことができます。
QuestionProには、相関係数の計算だけでなく、クロス集計、データの可視化、統計検定など、役立つデータ分析ツールが用意されています。これらの機能は、調査や変数の相互関係の理解に役立ちます。
変数間の関係を発見し、データ分析を進める準備はできましたか?今すぐQuestionProの無料トライアルを開始して、当社の調査ソフトがどのようにピアソン相関係数を簡単に求めることができるかをご覧ください。データ分析とリサーチを改善するチャンスをお見逃しなく。







