
スピアマンの相関係数: 定義
スピアマンの順位相関係数またはスピアマン相関係数は、順位相関(2つの変数間の順位の統計的依存性)のノンパラメトリック尺度です。
チャールズ・スピアマン(Charles Spearman)にちなんで命名され、ギリシャ文字の’ρ’(rho)で表記されることが多く、主にデータ分析に使用されます。
これは、2つのランク付けされた変数の間の関連性の強さと方向を測定します。しかしスピアマンの相関係数について話す前に、まずピアソンの相関について理解することが重要です。ピアソン相関は、対になったデータ間の線形関係の強さの統計的尺度です。
順位変数の計算と有意検定には、以下のデータ仮定が成り立つことが必要です:
データが上記の仮定を満たさない場合は、スピアマンの係数が必要です。スピアマンの相関係数を理解するためには、単調関数とは何かを知る必要があります。単調関数とは、独立変数の増加に伴って、決して減少しないか、あるいは決して増加しない関数のことです。単調関数は、下の画像を使って説明できます:
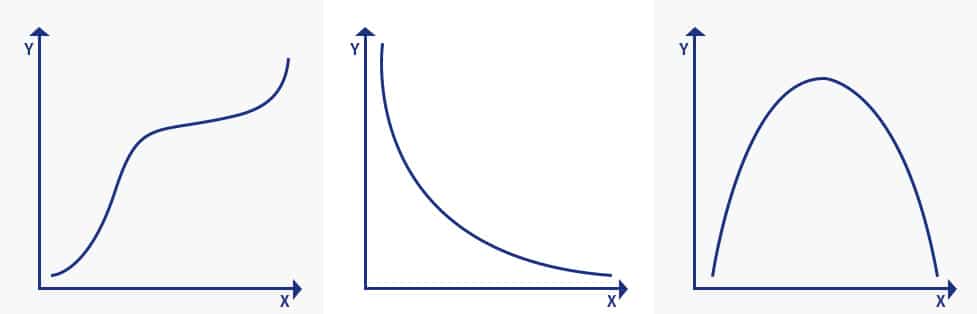
画像は単調関数の3つの概念を説明しています:
- 単調増加: 単調増加: ‘x’変数が増加し、’y’変数が決して減少しないとき。
- 単調減少: x’変数が増加し、’y’変数が増加しない場合。
- 単調でない x’変数が増加し、’y’変数が時々増加し、時々減少する場合。
単調関係は、ピアソン係数で使用される線形関係と比較すると、より制約が少ない。単調性はスピアマン相関係数の最終要件ではありませんが、変数間の関係が非単調であることがすでに分かっている場合、単調関係の強さと方向を実際に決定せずにスピアマンの相関を追求することは意味がありません。.
ここでは、
n= 2変数のデータポイントの数
di= “ith “要素のランクの差
Spearman 係数 ↪So_2374 は、+1 から -1 の間の値をとることができます、
- ⍴ 値が+1の場合は、ランクの完全な関連を意味します。
- ⍴ 値が0の場合は、ランクの関連性がないことを意味します。
- ⍴ 値が -1 の場合は、ランク間の完全な負の関連を意味します。
⍴ 値が0に近いほど、2つのランク間の関連性が弱くなります。
スピアマンの順位相関係数に進む前に、データの順位付けができなければなりません。1つの変数を増加させると、もう1つの変数が単調な関係に従うかどうかを観察することが重要です。
すべてのレベルで、2つの変数の値を比較する必要があります。計算の仕組みは次のとおりです:
歴史と地理の9人の学生の得点が、下の表に記載されています。
ステップ 1-得られたデータの表を作成します。
ステップ2-2つのデータ集合をランク付けすることから始めます。データの順位付けは、列の中で最も大きい数字に「1」、2番目に大きい数字に「2」というように、順位を割り当てることで達成できます。通常、最も小さい値が最も低い順位になります。これは、測定値の両方のセットに対して行う必要があります。
ステップ3- データセットに3番目の列dを追加します。ここでのdはランクの差を示します。例えば、最初の学生の物理の順位が3であり、数学の順位が5であれば、ランクの差は3です。4番目の列では、dの値を二乗します。
| 歴史 | 順位 | 地理 | 順位 | d | d二乗 |
| 35 | 3 | 30 | 5 | 2 | 4 |
| 23 | 5 | 33 | 3 | 2 | 4 |
| 47 | 1 | 45 | 2 | 1 | 1 |
| 17 | 6 | 23 | 6 | 0 | 0 |
| 10 | 7 | 8 | 8 | 1 | 1 |
| 43 | 2 | 49 | 1 | 1 | 1 |
| 9 | 8 | 12 | 7 | 1 | 1 |
| 6 | 9 | 4 | 9 | 0 | 0 |
| 28 | 4 | 31 | 4 | 0 | 0 |
| 12 |
ステップ4-dd乗の値をすべて足すと12(∑d乗)になります。
ステップ5ー式にこれらの値を挿入します。
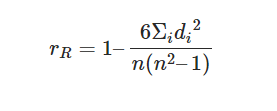
=1-(6*12)/(9(81-1))
=1-72/720
=1-01
=0.9
このデータのスピアマンの順位相関は0.9であり、前述のように、⍴の値が+1に近い場合は、順位が完全に関連しています。
QuestionProで相関係数を実施する方法
このセクションでは、アンケートのスピアマンの順位相関係数を実行する方法について説明します。
ステップ1:マイアンケートにアクセスし、アンケートを選択します。
ステップ2:分析の相関分析をクリックします。
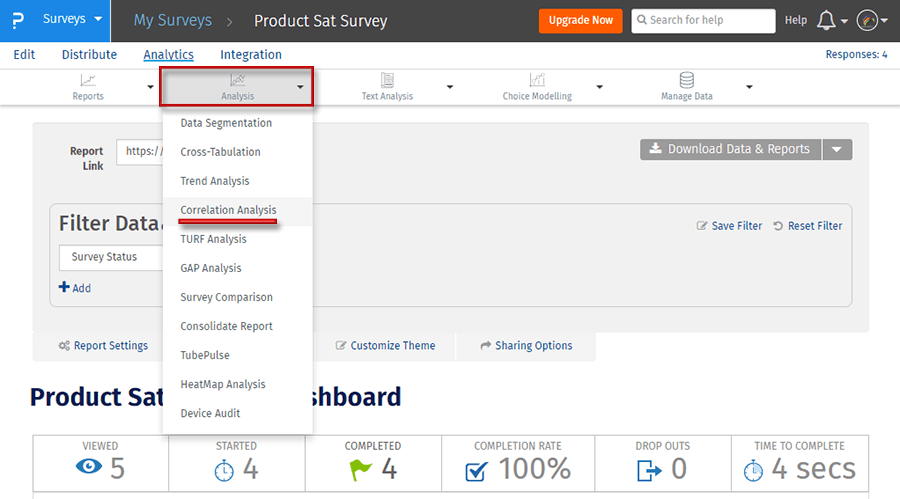
ステップ3:詳細なレポートを取得するには、スピアマン係数の生成をクリックします。
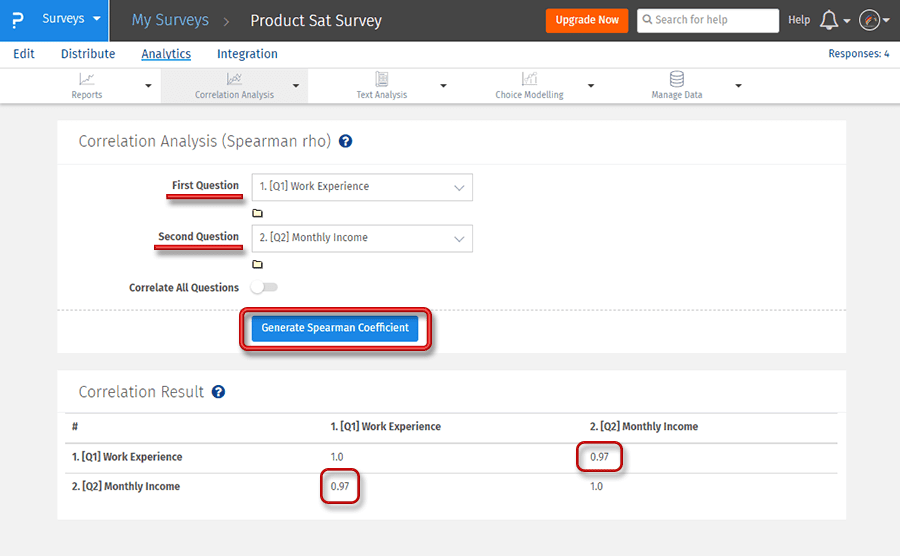
上記の例では、仕事経験と月収という2つの変数の関係を調べるために、スピアマン係数が使用されています。一般的な考え方は、月収は仕事の経験とともに増加するはずで、それは2つの変数の間に正の関連があるはずで、rs値が0.97であることによって証明されます。
詳細はこちら:ギャップ分析- 定義、手法、例付きテンプレート







