
相関は統計学やデータ分析における基本的な概念で、2つの変数の関係を理解するのに役立つ。強い正または負の相関が強調されることが多いが、ゼロ相関も同様に重要である。
これは変数間に線形関係がないことを意味する。言い換えれば、一方の変数の変化は他方の変数の変化を予測しないということである。
このブログでは、ゼロ相関の概念について、明確な定義、実例、そしてゼロ相関を判定する方法を紹介する。
ゼロ相関とは何か?
ゼロ相関とは統計用語で、2つの変数の間に線形関係がない状態を表す。2つの変数の相関がゼロのとき、一方の変数の変化は他方の変数の変化を予測しない。変数間の関係の程度と方向を測定する相関係数は、この場合正確にゼロである。
この相関関係を理解することは、統計分析において重要である。なぜなら、この相関関係は、互いに予測関係を持たない変数を特定するのに役立つからであり、統計モデルを構築したり、データ・パターンを解釈したりする際には極めて重要である。
なぜゼロ相関が重要なのか?
ゼロ相関は、統計学やデータ分析において重要な概念である:
独立性を示す
これは、互いに線形独立な変数を識別するのに役立つ。2つの変数の相関がゼロの場合、一方の変数の変化は、もう一方の変数の変化に関する情報を提供しない。これは、データの構造と変数間の関係(またはその欠如)を理解するために重要である。
統計モデルの改善
回帰分析やその他の統計モデルにおいて、従属変数と相関のある変数を含めると、ノイズが加わり、モデルの予測力が低下する可能性がある。このような変数を識別して除外することで、モデルを単純化し、より効率的にすることができ、より良いパフォーマンスと解釈可能性につながります。
この相関関係は誤解を避けるのに役立つ
この相関関係を理解することで、データの誤った解釈を防ぐことができる。
- 例えば、研究者が直感や最初の観察に基づいて、2つの変数の関係を誤って推測することがある。
相関係数を計算し、それがゼロであることがわかれば、線形関係が存在しないことが明確になり、誤った結論を避けることができる。
非線形の関係を強調する
非線形関係の可能性が浮き彫りになる。2つの変数の相関がゼロであったとしても、必ずしも無関係であるとは限らず、複雑で非線形な関係があるかもしれない。これを認識することで、非線形回帰やデータ変換など、他の方法を用いてさらに調査を進めることができます。
相関は実験計画の指針に役立つ
実験計画では、どの変数の相関がゼロであるかを知ることで、含める変数やコントロールする変数の選択を導くことができる。これは、無関係な変数の影響が最小化され、より明確で信頼性の高い結果につながる、よりロバストな実験計画に役立ちます。
可変的な行動を理解する
データセットに含まれる変数の挙動に関する洞察を提供する。金融分析では、どの資産が互いにゼロ相関であるかを理解することは、そのような資産を組み合わせることで全体的なリスクを減らすことができるため、ポートフォリオの分散に役立ちます。
仮説検証をサポート
仮説検定では、この相関関係を帰無仮説とすることが多い。
- 例えば、2つの変数が関連しているかどうかを検定する場合、帰無仮説は両者の相関がゼロであるとする。
これが真か偽かを確定することは、仮説の検証や反証に役立つ。
ゼロ相関の例とは?
ある変数の変化と別の変数の変化が一致しないという相関関係の例は、さまざまな分野で見られる:
研究分野
例科学論文の数と好きなアイスクリームのフレーバー
ある研究が、研究者の科学論文の数と好きなアイスクリームの味の関係を調査している。
研究者が発表する科学論文の数と、特定のアイスクリームの味に対する嗜好との間には、論理的な関連性はない。その結果、この2つの変数にはこのような相関関係があると予想される。
教育分野
例生徒の靴のサイズと数学の成績
ある教育研究では、生徒の靴のサイズと数学の成績に関係があるかどうかを調べている。
靴のサイズは身体的特徴であり、生徒の数学の成績には関係ない。したがって、靴のサイズと数学の成績の相関関係はゼロである可能性が高い。
ヘルスケア分野
例血液型と風邪の罹患率
血液型と1年間に風邪をひく回数に関係があるかどうかを調べた医療研究がある。
血液型は風邪の罹患頻度とは無関係であり、風邪はウイルスへの暴露や免疫力の強さなど、他の様々な要因に影響される。したがって、血液型と風邪の罹患率との相関関係はゼロであると予想される。
ゼロ相関を見極めるには?
ここでは、視覚的検査、統計計算、仮説検証、文脈分析を通じて、この相関関係を特定する方法を探る。
1.散布図を用いた目視検査
散布図は、2つの変数の関係を視覚的に評価するための効果的なツールである。
散布図を作成する:
- 一方の変数をx軸に、もう一方の変数をy軸に置く。
- データ・ポイントに識別可能なトレンドやパターンがないか探す。
相関関係を特定する:
- ポイントがランダムに散らばっていて、明確な傾向がない(上向きでも下向きでもない)場合は、相関関係があることを示唆している。
- ランダムな散らばりは、(直線であれ曲線であれ)どの直線もデータ点にうまくフィットしないことを意味する。
例
- 生徒の靴のサイズと数学の成績:靴のサイズと数学の成績をプロットし、トレンドのないランダムな点の散らばりを見た場合、これは相関関係がゼロであることを示す。
2.相関係数を計算する
ピアソン相関係数(r)は、線形相関の最も一般的な尺度である。
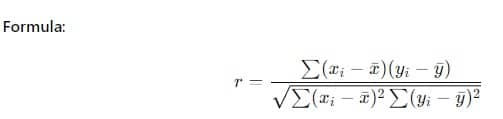
ステップ
- 2つの変数の対になるデータ点を集める。
- 各変数の平均(平均値)を求める。
- 各データ点が平均からどのくらい離れているかを計算する。
- 各ペアの偏差を掛け合わせ、その積を合計する。
- 式を使って相関係数を求めなさい。
相関関係の解釈:
0に近い値: 𝑟 rが0に近い場合は、変数間の線形関係がほとんどないことを示す。
例
- 靴のサイズと数学の成績:算出された ᵅ がほぼ0の場合、相関がゼロであることが確認される。
3.仮説検証を行う
統計的仮説検定は、観察された相関係数がゼロから有意に異なるかどうかを決定することができる。
ステップ
- 帰無仮説:相関係数がゼロであると仮定する。
- 代替仮説:相関係数がゼロではないと仮定する。
- 検定統計量の計算:相関係数についてt検定を使用する。
- p値を決定する:p値を有意水準(例えば0.05)と比較する。
相関性ゼロ:
- p値が有意水準より大きい場合は、帰無仮説を棄却せず、相関はゼロから有意に異ならないことを示唆する。
例
- 血液型と風邪の発生率:血液型と風邪の罹患率の相関を調べ、p値が高ければ、観察された相関は統計的に有意ではないことを示し、相関ゼロを支持する。
4.文脈分析を理解する
相関結果を解釈するためには、変数の文脈と理論的背景を理解することが不可欠である。
ステップ
- 変数を調べる: 変数の性質と予想される関係を検討する。
- 分野の知識を応用する: 分野の知識を使って、ある関係が予想されるかどうか仮説を立てる。
相関性ゼロ:
- 理論や先行研究が論理的な関係を示唆しないのであれば、この相関関係の発見を支持することになる。
例
- 血液型と風邪の罹患率:血液型が風邪の罹りやすさに影響を与えないことを知っていれば、相関はゼロと解釈することができる。
負の相関 vs 正の相関 vs ゼロの相関
相関は、2つの変数の間の関係の強さと方向を記述する統計的尺度である。ここでは、負の相関、正の相関、ゼロの相関について詳しく説明する:
正の相関
- 定義 正の相関は、2つの変数が同じ方向に動くときに起こる。一方の変数が増加すると他方の変数も増加し、一方が減少すると他方も減少する。
- 例身長と体重の関係。一般的に、身長が高くなると体重も増加する傾向がある。
- グラフ表現:散布図では、点は左から右に向かって上向きに傾斜する線の周りに集まる傾向がある。
負の相関
- 定義 負の相関は、2つの変数が逆方向に動くときに起こる。一方の変数が増加すると、他方の変数は減少し、逆もまた同様である。
- 例 勉強時間とテストのミス数の関係。一般的に、勉強時間が長くなると、ミスの数は減る。
- グラフ表現:散布図では、点は左から右へ下降傾斜する線の周りに集まる傾向がある。
相関ゼロ
- 定義: 2つの変数の間に関係がないことを示す.一方の変数の変化は、もう一方の変数の変化を予測しない。
- 例 靴のサイズと知能指数(IQ)の関係。この2つの変数の間には論理的なつながりはない。
- グラフ表現: 散布図では、点はランダムに分布し、識別可能なパターンや傾きはない。
QuestionProは相関分析にどのように役立ちますか?
堅牢な調査プラットフォームであるQuestionProは、相関分析を効果的に行うための包括的なツールを提供しています。ここでは、相関分析を行う際にQuestionProがどのように役立つかをご紹介します:
容易なデータ収集
QuestionProは、ユーザーフレンドリーなアンケート作成ツールにより、データ収集プロセスを簡素化します。アンケートを作成して配布し、関心のあるさまざまな変数に関する定量データを収集できます。このプラットフォームはさまざまな質問タイプをサポートしており、詳細かつ関連性の高いデータを効率的に収集できます。
自動データ分析
データが収集されると、QuestionPro には相関分析のための分析ツールが組み込まれます。2つの変数間の線形関係の強さと方向を測定する相関を簡単に計算することができます。線形相関係数の範囲は-1~1です:
- 1は完全な正の相関を示す。
- -1は完全な負の相関を示す。
- 0は相関なしを示す。
視覚的表現
QuestionProは、相関分析の結果を解釈するのに役立つ可視化ツールを提供します。散布図や相関行列を生成して、変数間の関係を明確にグラフ表示することができます。この視覚的な支援は、傾向やパターンをすばやく特定するために非常に重要です。
パターンと傾向の特定
QuestionProの相関分析を用いて、研究者は変数間の相関(正、負、ゼロ)を観察した:
- 正の相関:両方の変数が同じ方向に動く。例えば、広告費の増加は売上の増加と相関する可能性がある。
- 負の相関:変数が逆方向に動く傾向がある。例えば、スクリーン利用時間の増加は学業成績の低下と相関するかもしれない。
- ゼロ相関:変数間に関係が存在しない。例えば、在学年数と名前の文字数は相関しないかもしれない。
実践的応用
QuestionProの相関分析は、次のようなさまざまな実用的なアプリケーションに使用できます:
- 市場調査:広告宣伝費と販売実績の相関関係により、マーケティング・キャンペーンの効果を測定する。
- ヘルスケア 薬の使用量と血圧値などの患者の転帰との関係を評価する。
- 教育学習時間と成績の相関から、学習習慣が学業成績に及ぼす影響を調べる。
結論
2つの変数間の相関がゼロであることは、線形関係がないことを意味し、ある変数の変化が別の変数の変化に対応しないことを示す。相関係数を計算し、散布図によってデータを視覚化することで、研究者は変数が相関しているか、正の相関があるか、負の相関があるか、あるいはこの相関があるかを正確に判断することができる。
アンケートの相関分析にQuestionProを使用すると、変数間の意味のある関係を明らかにする強力な方法が得られます。QuestionProの直感的なインターフェイス、高度な分析ツール、包括的なレポート機能を活用することで、相関分析を効率的に実施し、データから貴重な洞察を引き出すことができます。詳細については、今すぐQuestionProにお問い合わせください!







