回帰分析とは、従属変数と一連の独立した説明変数の関係を調査または推定するための、おそらく最も広く使われている統計手法です。
また、質的研究手法において、多数の変数をモデル化し分析するために利用される様々なデータ分析手法の総称としても使用される。 回帰法では、従属変数が予測因子または説明要素であり、従属変数が結果または特定のクエリに対する応答である。
回帰分析。定義
回帰分析は、データのモデル化や分析によく使われます。 調査アナリストの多くは、変数間の関係を把握し、さらに正確な結果の予測に活用するために利用しています。
例 – ある清涼飲料水メーカーが、製造部門を新しい場所に拡張したいと考えたとする。 その前に、収益モデルとそれに影響を与える様々な要因を分析したいと考えています。 それゆえ、同社は
オンライン調査
を、特定のアンケートで実施。
回帰分析を使ってから、会社は調査結果を分析し、電力などのさまざまな変数と収益の関係を理解することが容易になります – ここでは収益を従属変数とします。 さらに、価格、従業員数、物流など、さまざまな独立変数と売上との関係を把握することで、さまざまな要因が会社の売上と利益に与える影響を推定することができます。
調査研究者はしばしばこの手法を用いて、関心のある異なる変数間の相関関係を調べ、発見する。 を提供しています。 異なる独立変数が従属変数に及ぼす影響を測定する機会である。 回帰分析とは、多数の独立変数を表形式で並べ、その従属変数への影響を検証または計算することで、調査研究者のさらなる労力を節約する手法である。 新しい製品を評価するために、さまざまな種類の分析法が広く用いられています。
ビジネスアイデアを
を考え、十分な情報を得た上で決断する。
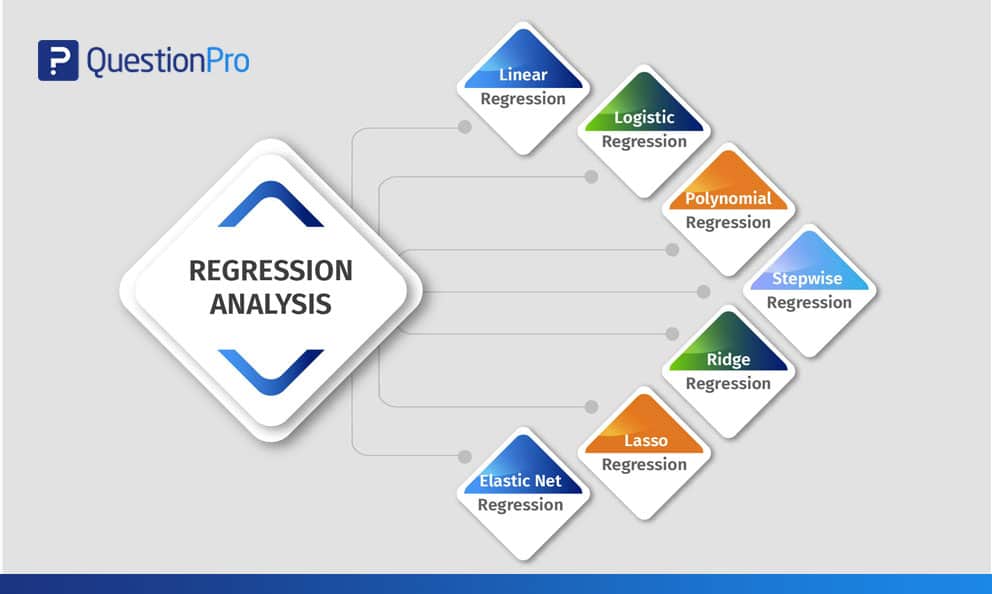
回帰分析の種類
研究者は通常、まず線形回帰とロジスティック回帰を学ぶことから始めます。 この2つの方法が広く知られ、適用が容易なため、多くのアナリストはモデルが2種類しかないと考えている。 各モデルには得意分野があり、特定の条件を満たした場合に能力を発揮する。 このブログでは、列挙された大量のデータを様々な形式で解釈するために、よく使われる7種類の回帰分析手法を解説しています。
線形回帰分析
予測モデル学習時に最初に取り上げられたエリート回帰分析手法の一つであり、最も広く知られたモデリング手法の一つである。 ここで、従属変数は連続的であり、独立変数は連続的または離散的であることが多く、線形回帰線がある。
重回帰では複数の独立変数があり、単回帰では独立変数は1つだけであることに注意してください。 したがって、線形回帰は、独立変数と従属変数の間に線形関係がある場合にのみ使用するのが最善です。
例 マーケティング・キャンペーン、価格設定、販売促進などの効果を測定するために、線形回帰を使用することができます。 例えば、スポーツ用品を販売する企業が、自社製品のマーケティングやブランディングに投じた資金が、実質的なリターンにつながっているかどうかを把握したいとします。 線形回帰は、結果を解釈するのに最適な統計手法である。 線形回帰の最も良い点は、各マーケティングやブランディング活動の不明瞭な影響を分析し、かつ売上を規制する構成要素の可能性をコントロールするのにも役立つということです。 もし会社が同時に2つ以上の広告キャンペーンを行っている場合、例えばテレビで1つ、ラジオで2つの広告を行う場合、線形回帰はこれらの広告を一緒に行うことによる独立した影響と組み合わせた影響を簡単に分析することができます。
ロジスティック回帰分析
ロジスティック回帰は、以下の確率を求めるためによく使われます。
イベント=成功
と
イベント=失敗
. 従属変数が0/1, True/False, Yes/No のようなバイナリであるときはいつでも、ロジスティック回帰が使用されます。 このように、ロジスティック回帰はどちらかの分析に使われると言えます。
クローズドエンド型設問
アンケートで数値回答を求める質問など。
なお、ロジスティック回帰は、線形回帰のように従属変数と独立変数の間に線形関係を必要としません。 ロジスティック回帰は、非線形対数変換を適用してオッズ比を予測するため、従属変数と独立変数の間の様々な種類の関係を容易に扱うことができます。
例 ロジスティック回帰は、ビジネスデータのモデリングにおいて、カテゴリデータ、特にバイナリ応答データの分析に広く用いられている。 より頻繁にロジスティック回帰が使用されるのは、従属変数がカテゴリである場合、例えば、ある人が行った健康被害が本物か(1)、詐欺であるかを予測したり、腫瘍が悪性か(1)を理解したりするためです。 企業はロジスティック回帰を用いて、年齢、収入、性別、人種、居住州、過去の購入履歴などをもとに、特定の層の消費者が自社製品を購入するか、競合他社から購入するかを予測することができます。
多項式回帰分析
多項式回帰は、曲線的なデータを分析するためによく使われ、これは独立変数のべき乗が1以上である場合に起こります。 この回帰分析法では、最適な直線は決して「直線」ではなく、常にデータポイントにフィットする「曲線」となる。
なお、多項式回帰は、指数を持つ変数が少なく、指数を持たない変数が少ない場合に使用するのがよいでしょう。 さらに、非線形分離可能なデータのモデリングが可能で、各変数の正確な指数を自由に選択でき、モデリング機能を完全に制御することも可能です。
例 多項式回帰と応答曲面分析との組み合わせは、マルチソースフィードバック研究でよく使われる高度な統計的アプローチと考えられている。 多項式回帰は、従属変数と独立変数の関係が曲線的である金融や保険関連産業で主に使用されます。 例えば、ある人が、確定した金額を稼ぐのにどれだけの時間がかかるかを判断して、予算支出計画を立てたいとします。 その人の収入と支出を考慮した多項式回帰により、その人が特定の金額を稼ぐために必要な正確な時間を簡単に決定することができます。
ステップワイズ回帰分析
これは、推定係数のt統計量に依存する変数を追加または削除することによって、統計モデルを構築する半自動化プロセスである。 ステップワイズ回帰を正しく使えば、どんな方法よりも強力なデータを手元に置くことができます。 多数の独立変数を扱う場合に有効です。 変数をランダムにつつくことで、解析モデルを微調整しているだけなのです。 ステップワイズ回帰分析は、独立変数が複数ある場合に使用することが推奨されており、独立変数の選択は、人手を介さず自動的に行われる。
なお、ステップワイズ回帰モデリングでは、変数は説明変数のセットから追加または減算される。 推定された係数の検定統計量に応じて、追加・削除される変数のセットが選択される。
例 年齢、体重、体表面積、高血圧の期間、基礎脈拍、ストレス指数など、いくつかの独立変数があり、それに基づいて血圧への影響を分析するとします。 ステップワイズ回帰では,独立変数の最適なサブセットが自動的に選択される.それは,それ以上進むために変数を選択しないことから始めるか(一度に1つの変数を追加するので),モデル内のすべての変数から始めて後方に進む(一度に1つの変数を除去する). したがって、回帰分析を使って、各変数または一群の変数が血圧に与える影響を計算することができます。
リッジ回帰分析
リッジ回帰は、多重共線性データ(独立変数が高い相関を持つデータ)を分析するために用いられる通常の最小二乗法に基づくものです。 共線性とは、変数の間に直線に近い関係があることとして説明できる。 多重共線性がある場合、最小二乗法の推定値は不偏となるが、両者の差が大きければ、真の値から大きく離れている可能性がある。 しかし、リッジ回帰では、より信頼性の高い推定値を提供することを動機に、回帰推定値にある程度のバイアスを加えることで標準誤差を排除している。
なお、リッジ回帰の前提条件は、最小二乗回帰と同様であり、唯一の違いは正規性である。 リッジ回帰では係数の値が狭まっているが、ゼロになることはなく、変数の選択ができないことが示唆される。
例 例えば、あなたが近くのイベントでライブをする2人のギタリストに夢中になって、どちらがより優れたギタリストなのかを知るために、彼らの演奏を見に行ったとします。 しかし、いざ演奏が始まると、両者が同時に黒音符と青音符を弾いていることに気がつく。 大音量で速弾きしたときに、その中で最も音に影響を与えるギタリストを見つけることは可能なのでしょうか? 両者が異なる音を奏でているため、両者を区別することは実質的に困難であり、多重共線性の最たるもので、その結果、係数の標準誤差を増大させる傾向がある。 リッジ回帰は、このような場合の多重共線性に対応し、バイアスや縮約推定を含めて結果を導出する。
ラッソー回帰分析
Lasso (Least Absolute Shrinkage and Selection Operator) は、リッジ回帰と似ていますが、リッジ回帰で使用する二乗バイアスの代わりに絶対値バイアスを使用します。 1989年に従来の最小二乗法による推定に代わる手法として開発され、データに多数の独立変数がある場合のオーバーフィッティングに関連する問題の大半を解決することを意図しています。 Lassoは、変数の選択とソフトな閾値に沿った正則化の両方を行う機能を備えています。 ラッソ回帰を適用することで、定量的な反応を分析する際に、予測誤差を最小化するための予測変数の部分集合を容易に導き出すことができるようになります。
なお、ラッソーモデルでは、縮小後にゼロになった回帰係数はモデルから除外される。 逆に、0より大きな値を持つ回帰係数は、説明変数が定量的、カテゴリー的、またはその両方である場合、応答変数と強く関連しています。
例 ある自動車メーカーが、米国における自動車の平均燃費について調査分析を行いたいとします。 サンプルとして、32の車種と自動車設計の10の特徴(シリンダー数、排気量、総馬力、後軸比、重量、1/4マイルタイム、対エンジン、トランスミッション、ギア数、キャブレター数)が選ばれました。 応答変数mpg(miles per gallon)の相関が、重量、排気量、シリンダー数、馬力などのいくつかの変数と非常に相関があることがおわかりいただけると思います。 を活用することで、問題を分析することができます。
glmnet
パッケージを使用し、特徴選択にはlasso回帰を使用しています。
エラスティック・ネット回帰分析
L1ノルムとL2ノルムで学習したリッジ回帰モデルとラッソ回帰モデルの混合モデルである。 エラスティックネットは、相関の強い予測変数が一緒にモデルに入ったり出たりする傾向があるグループ化効果をもたらす。 予測変数の数が観測値の数よりはるかに多い場合、エラスティック・ネット回帰モデルを使用することが推奨されます。
なお、elastic net回帰モデルは、lasso回帰モデルの変数部分がデータに依存しすぎて不安定になったため、lasso回帰モデルのオプションとして誕生した。 エラスティックネット回帰を使うことで、統計学者はリッジ回帰とラッソ回帰のペナルティをオーバーブリッジして、両方のモデルからベストなものを得ることができるようになりました。
例 白血病に関するマイクロアレイデータセット(LEU)を入手した臨床研究チームは、提示された遺伝子サンプルの発現レベルに基づき、白血病の種類を予測する診断ルールを構築することに関心を持った。 彼らが持っていたデータセットは、多数の遺伝子と少数のサンプルから構成されていました。 さらに、学習用サンプルとして、1型白血病(急性リンパ性白血病)と2型白血病(急性骨髄性白血病)に感染したサンプルも用意されました。 学習データに対して、モデルフィッティングと10重CVによるチューニングパラメータの選択を行った。 そして、必要な結果を得るために、テストデータに対して予測値の平均二乗誤差を計算することで、それらの手法の性能を比較した。
市場調査での活用
大きく3つのマトリックスに着目して市場調査を実施。
顧客満足度
カスタマー・ロイヤリティ、カスタマー・アドボカシーの3つです。 これらのマトリックスは、顧客の健康状態や意向を知ることはできても、ポジションを改善する方法を知ることはできないことを忘れてはならない。 したがって、消費者の不満の理由を尋ねることを意図した詳細な調査アンケートは、実用的な洞察を得るための方法であることは間違いありません。
しかし、人は自分のやる気ややる気を出したり、満足度や不満足度を表現するのに苦労することが多いことが分かっています。 さらに、人々は常に価格やパッケージなど、いくつかの合理的な要素を過度に重視します。 全体として、市場調査における予測分析・予測ツールとして機能する。
予測ツールとして使用する場合、回帰分析では、外部市場のデータを考慮して組織の売上高を決定することができます。 ある多国籍企業が、GDP(国内総生産)やCPI(消費者物価指数)など、さまざまな要因が収益モデルに与える影響を把握するために、市場調査を実施した。 もちろん、予測されるマーケティング指標を考慮した回帰分析によって、将来の四半期、さらには将来の年に生み出されるであろう暫定的な収益を予測することができた。 しかし、将来的に進めば進むほど、データの信頼性が低くなり、誤差が大きくなります。
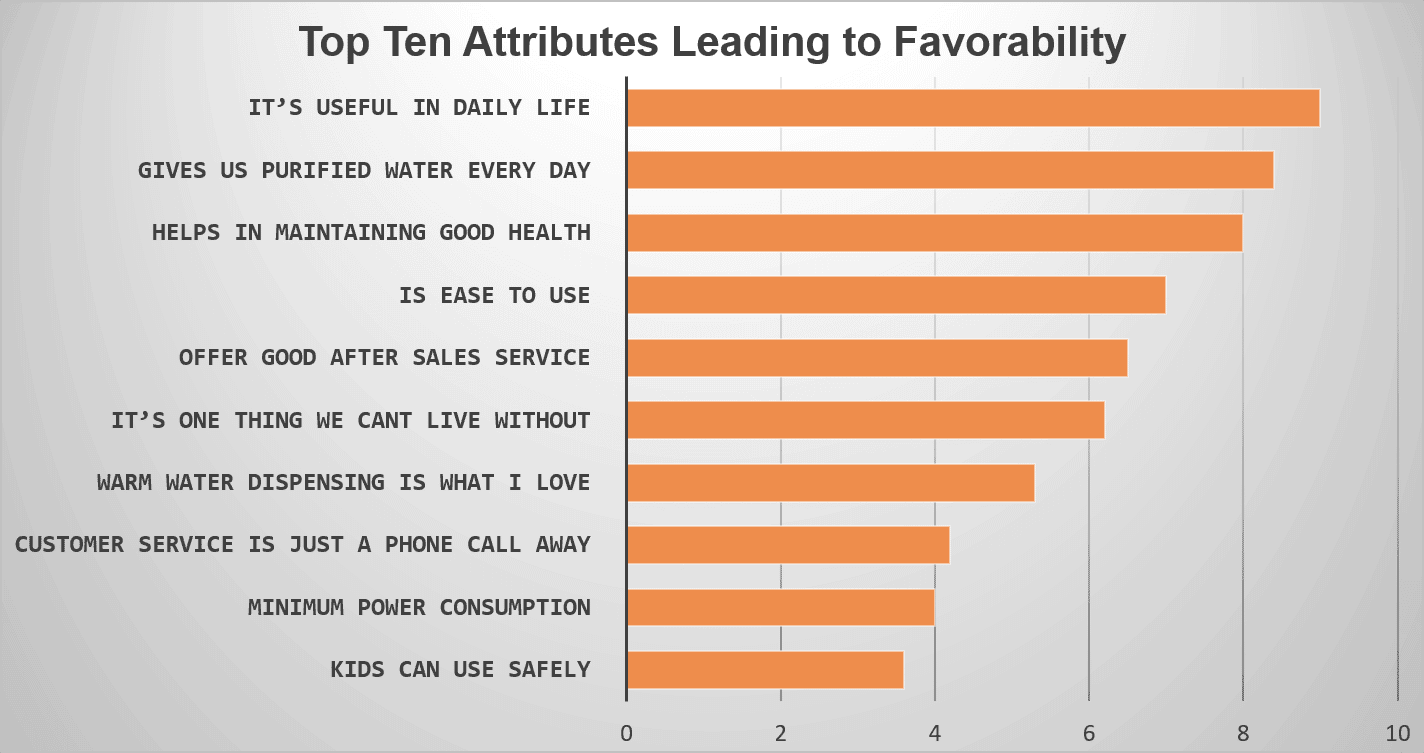
例 ある浄水器メーカーは、ブランドの好感度につながる要因を把握したいと考えていました。 アンケートは、既存顧客や見込み客にアプローチするための最適なメディアでした。 大規模な消費者調査を計画し、最適な調査ツールを用いて控えめなアンケートを作成しました。 この調査では、ブランド、好感度、満足度、不満足度などに関する多くの質問が効果的に行われました。 アンケートで最適な回答を得た後、回帰分析によりブランド好感度の要因上位10項目を絞り込みました。 下の画像にある10個の属性はすべて、その浄水器ブランドの好感度に影響を与える重要なものであることが、何らかの形で強調されています。
ExcelやSPSSを使って回帰分析を行うのは簡単ですが、その一方で、データを解釈する上で4つの数字の重要性を理解する必要があります。
4つの数値のうち、最初の2つの数値は、回帰モデルそのものに直接関係する。
F値。調査モデルの統計的有意性を測定するのに役立つ。 F値が0.05より有意に小さい場合は、より意味のある値とみなされることを覚えておいてください。 0.05 以下の F-Value は、調査分析の結果が偶然のものではないことを保証します。
- R-2乗。独立変数が従属変数の移動量を説明しようとする値である。 R2乗の値が0.7であると考えると、これは従属変数の動きの70%がテストされた独立変数で説明できることを意味します。 つまり、私たちが手にする調査分析のアウトプットは、高い予測性を持ち、正確であると考えることができるのです。
他の2つの数値は、回帰分析を解釈する際に、それぞれの独立変数に関連するものである。
- P-Value(ピーバリュー)。F値と同様に、P値も統計的に重要な意味を持つ。 さらにここでは、独立変数の効果がどの程度関連性があり、統計的に有意であるかを示している。 もう一度、0.05以下の値を求めます。
- 4番目の数字は、変数の影響を測定した後に達成された係数に関するものである。 例えば、複数の独立変数を検定して、「他の独立変数が同じ値で停滞しているときに、独立変数(我々が検討している変数)が1つ増えたら、従属変数は何倍になると予想されるか」を示す係数を得ます。 いくつかのケースでは、単純な係数は、各独立変数が従属変数を動かす、または変化をもたらすことへの寄与を示す標準化された係数に置き換えられます。
オンライン調査で回帰分析を使用するメリット
予測分析にアクセスできるようになります。
回帰分析を使って、ビジネス・サーベイの結果を把握する方法をご存知ですか?
ビジネス・サーベイ
将来のチャンスとリスクを明らかにする力を手に入れたようなものだと思いませんか?
例えば、あるテレビ広告の枠を見た後、そのデータから正確な企業数を予測し、その枠の最大入札額を推定することができます。 金融・保険業界では、より正確な計画や意思決定のために、調査データの回帰分析による傾向や機会の特定に多くを依存しています。
業務効率の向上
ビジネスでは、回帰分析を使ってビジネスプロセスを最適化していることをご存知でしょうか。
例えば、新しい製品ラインを発売する前に、企業は消費者調査を実施します。
消費者調査
その製品の生産、包装、流通、消費に及ぼすさまざまな影響をよりよく理解することを目的としています。 データ駆動型の先見性は、意思決定から当て推量や仮説、社内政治を排除するのに役立ちます。 業務効率と収益に影響を与える分野をより深く理解することで、より良いビジネスの最適化につながります。
意思決定を定量的に支援する。
ビジネス調査現代は、財務、収益、経営、購買などに関する多くのデータが生成され、経営者は情報に基づいたビジネス上の意思決定を行うために、さまざまなデータ分析モデルに大きく依存しています。
例えば、回帰分析では、企業が十分な情報に基づいて戦略的な人員配置を決定するのに役立ちます。 従業員エンゲージメント調査、従業員満足度調査、雇用主改善調査、従業員退社調査などの従業員調査を実施し、その結果を解釈することで、従業員と企業の関係性をより深く理解することができます。 また、組織の労働文化、労働環境、生産性に影響を与える可能性のある特定の問題について、公平に把握することができます。 さらに、インテリジェントなビジネス指向の解釈により、膨大な生データを実用的な情報に落とし込み、より多くの情報に基づいた意思決定を行うことができます。
直感で起こるミスを防ぐ。
回帰分析の使い方を知ることで
回帰分析の使い方
また、調査結果の解釈については、経営陣の意思決定のための事実関係の裏付けを容易にすることができます。 しかし、判定に誤りがないようにするのにも役立つことをご存知でしょうか?
例えば、あるショッピングモールの店長が、閉店時間を延ばせば売上が上がると考えたとする。 回帰分析では、売上高が増加しても、労働時間の延長に伴う営業費用の増加を支えるには十分でないと予測し、この考えを否定しています。