- Dateien hochladen (Bilder/Multimedia/Ton)
- Anzahl der Fragen pro Umfrage
- Umfrage mit MS Word erstellen
- Live-Online-Umfragen bearbeiten
- Umfrageblocks
- Umfrageblock-Randomizer
- Fragen-Randomizer
- Skalenbibliothek
- Monadische Tests
- Sequentielle monadische Tests
- Extraktionsunterstützung für Fragetypen mit Bildauswahl
- Vergleichstest
- Custom validation messages
- Erstellen von Umfragen mit QxBot
- Testing Send
- Survey Preview Options
- Online Umfrage erstellen: Standard-Fragetypen
- Erweiterte Fragetypen
- Multiple-Choice-Fragen (Geschlossen)
- Text Frage- Kommentarfeld
- Matrix multi-point scales question type
- Rangordnung
- Smiley-Bewertungsfragen
- Bildfragetyp
- Datum und Uhrzeit Fragetyp
- Captcha-Frage
- Net Promoter Score question type
- Van Westendorp's price sensitivity question
- Auswahlbasierte Conjoint Analyse
- Seite-an-Seite-Matrix
- fragetyp medizin schmerzemfinden studie
- Vorhersage-Antwortoptionen - QuestionPro AI
- Präsentationstext
- Multiple Choice: Wählen Sie eine aus
- Multiple Choice: Wählen Sie viele aus
- Page Timer
- Frage zur Kontaktinformation
- Matrix-Mehrfachauswahlfrage
- Matrix-Tabellenkalkulationsfrage
- Geschlossener Fragetyp - Kartensortierung
- Flex Matrix
- Text Schieberegler - Fragentyp
- Emojis als Bewertung einrichten möglich?
- Rank Order - Drag and Drop
- Bipolare Matrix - Schieberegler
- Bipolare und Likert-Matrix-Fragen
- Gabor-Granger-Preismethode
- Verifizierte Signatur - Fragetyp
- Fragetyp: Sternenbewertung
- Push To Social: Feedback in sozialen Medien “pushen"
- Frage-Dateien hochladen
- Konstantsummen-Fragetyp hinzufügen
- Video-Insights
- Plattform Verbinden
- Rekrutierung von Gemeinden
- TubePulse Videobewertung
- Offener Fragetyp - Kartensortierung
- Map Question Type
- Antwort-Typ und -Layout
- Fragen nachbestellen
- Frage-Tipps
- Textfeld-Anzeige
- Offene Texteinstellungen für die Kommentar-Box
- Option Sonstiges hinzufügen
- Matrix - Einstellungen
- Bildbewertungsfragen-Einstellungen
- Skalierungsoptionen
- Konstantensumme - Einstellungen
- Standard ausgewählte Option
- Exklusive Optionsvalidierung für Multiple-Choice
- Fragen mit erforderlicher Validierung
- Validierung - Einstellungen
- Validierung entfernen
- Fragenseparatoren
- Fragecodes
- Seitenumbrüche
- Einleitungstext mit Akzeptanz-Kontrollkästchen
- RegEx-Validation
- Verwendung der Fragebibliothek
- Embed Media
- Slider Start Position
- Answer Display Order - Alternate Flip
- Auto-focus für Matrix-Fragen
- Textvalidierungen
- Numeric Input Settings- Spreadsheet
- Antwortgruppen hinzufügen
- Fragen ausblenden
- Mehrere Dateien – Datei anhängen/hochladenj
- Eingabe im Textfeld - Tastaturtyp
- Randomisierung von Antwortoptionen
- Alternate colors
- Conjoint-Analyse - FAQ zur Umsetzung bewährter Verfahren
- Limits für Bilder/Multimedia-Dateien
- Decimal Separator Currency Format
- Deep Dive
- Logo hinzufügen
- Individuelles Design
- Anzeigeeinstellungen und Umfrage Steuerung
- Automatischer Fragevorschub (Auto-Advance)
- Fortschrittsbalken
- Automatische Fragennummerierung
- Symbolleiste "Soziales Netzwerk"
- Browser-Titel
- Umfrage ausdrucken - Word/PDF-Datei erzeugen
- Navigationsschaltflächen der Umfrage
- Barrierefreies Thema
- Back and Exit Navigation Buttons
- Anzeigemodus - Fokus
- Umfrage Anzeigemodus
- Umfragelayout – Visuell
- Fernseher Integration
- Telly-Integration
- Arbeitsbereich URL
- Klassisches Layout
- Verzweigungs- oder Skip-Logik
- Zusammengesetzte Verzweigungslogik
- Zusammengesetzte oder verzögerte Verzweigung
- Dynamische Quoten-Kontrolle bei Online Umfragen
- Dynamische Text- oder Kommentarfelder
- Extraktionslogik
- Fragen ein- und ausblenden
- Dynamische Show / Hide-Logik
- Bewertungslogik: sofortige Ergebnisanzeige
- Scoring Logik: Net Promoter Score
- Piping-Text (Weiterleitungstext)
- Umfragen verketten
- Schleifenlogik
- Verzweigung zum Beenden der Umfrage
- Logik Operatoren
- Ausgewählte N aus M-Logik
- JavaScript-Logik Syntax-Referenz
- Block-Flow
- Block-Looping
- Syntax-Referenz der Bewertungs-Engine
- Logik "Immer extrahieren" und "Nie extrahieren
- Matrix Extraction
- Gesperrte Extraktion
- Dynamische benutzerdefinierte Variablenaktualisierung
- Erweiterte Randomisierung
- Beispiele für benutzerdefinierte Skripts
- Benutzerdefiniertes Scripting
- Survey Logic Builder - AI
- Befragungseinstellungen
- Sicherheit: Optionen speichern und fortfahren
- Mehrfachabstimmung verhindern
- Schließen, beenden und deaktivieren einer Umfrage
- Admin-Bestätigungs-E-Mail
- Aktionsaufrufe
- Session Timeout bei Online Umfragen
- Abschlussoptionen
- Spotlight-Report
- Antwort ansehen / drucken
- Suchen & Ersetzen
- Einrichten einer Timeout-Option
- Umfragen mehrfach auf einem Gerät ausfüllen
- Text Input Size Settings
- Admin Confirmation Emails
- Datum und Uhrzeit der Umfrage-Schließung
- Standortdaten des Befragten
- Überprüfungsmodus
- Überprüfen, bearbeiten und drucken von Antworten
- Geokodierung
- Fortschrittsanzeige - Dynamischer Stil
- Quotensteuerung | Antworten begrenzen
- Altersüberprüfung
- Umfrageoptionen | Werkzeuge
- Umfrage-Authentifizierung
- Globaler Passwortschutz
- Umfrage-Authentifizierung nur mit E-Mail-Einladungen
- E-Mail Passwort
- Verwendung der Teilnehmer-ID. Login und Sicherheit
- Umfrageauthentifizierung Benutzername/Passwort
- SSL Verschlüsselung
- Facebook-Authentifizierung für Online Umfrage
- Umfrage-Authentifizierung - SAML SSO
- Verschlüsselte Medien-URLs
- Umfrage-URL
- Benutzerdefinierte URL
- E-Mail-Einladungsvorlagen erstellen
- Seriendruck/Personalisierung von E-Mails
- E-Mail-Einstellungen | Absender-Name oder E-Mail
- E-Mail-Listen filtern
- Umfrage-Erinnerungen
- Batch-Export: E-Mail-Listen für externe Verarbeitung
- E-Mail-Status
- spam index online umfragen
- SMS-Einladung erstellen
- Auswertungen von Telefon- und Papier-Umfragen
- Manuelles Hinzufügen von Antworten
- SMS-Preisgestaltung
- Frage in E-Mail einbetten
- E-Mail-Listen löschen
- Mehrsprachiger E-Mail-Verteiler
- Mail-Server-Integration via SMTP Relay
- Antwort-E-Mail-Adresse
- Domain-Authentifizierung
- Fehlerbehebung bei der E-Mail-Zustellung
- QR Code
- Email Delivery and Deliverability
- Offline App Themen
- ${WEB} - Loop-Umfragen
- Mobile App
- Kiosk-Modus
- App-Daten synchronisieren
- Rückmeldung überprüfen / PDF auf Offline-App drucken
- Feld & Geräteprüfung
- Variablen für Offline-Geräte
- Manuelle Synchronisierung von Antworten
- Geräteschlüssel - Details zur Gerätehardware
- Gesichtserkennung im Kiosk-Modus
- Text to Speech
- Push-Benachrichtigung
- Offline-App – Best Practices
- Bericht zum Umfrage-Dashboard
- Teilnehmerstatistiken und Rücklaufquoten
- Drop-Out-Analyse
- Erweiterte Optionen: Banner-Tabelle
- TURF-Analyse
- Trendanalyse
- Korrelationsanalyse
- Umfragenvergleich
- GAP-Analyse
- Mittelwert-Kalkulation
- Gewichteter Mittelwert
- Spinnendiagramm
- Cluster-Analyse
- Dashboard-Filter
- QuestionPro-Datapad
- Dashboard - Download-Optionen
- HotSpot-Bild-Tests
- Heatmap Analysis
- Gewichtete Rangfolge
- Antwortoptionen für die Kreuztabellengruppierung
- A/B-Tests in QuestionPro-Umfragen
- Datenqualität
- Antwort für Datenqualitätskennzeichen beenden
- Matrix-Heatmap-Diagramm
- TURF Reach Analysis
- Sicherheit: Passwortgeschützte Umfragen
- Gewichtung - Eliminierung von Stichprobenverzerrungen
- Column proportions test
- Response Identifier
- Conjoint Analysis (Discrete Choice Module) Designs
- Conjoint Teil-Wert-Berechnung
- Conjoint-Analyse - Berechnungen / Methodik
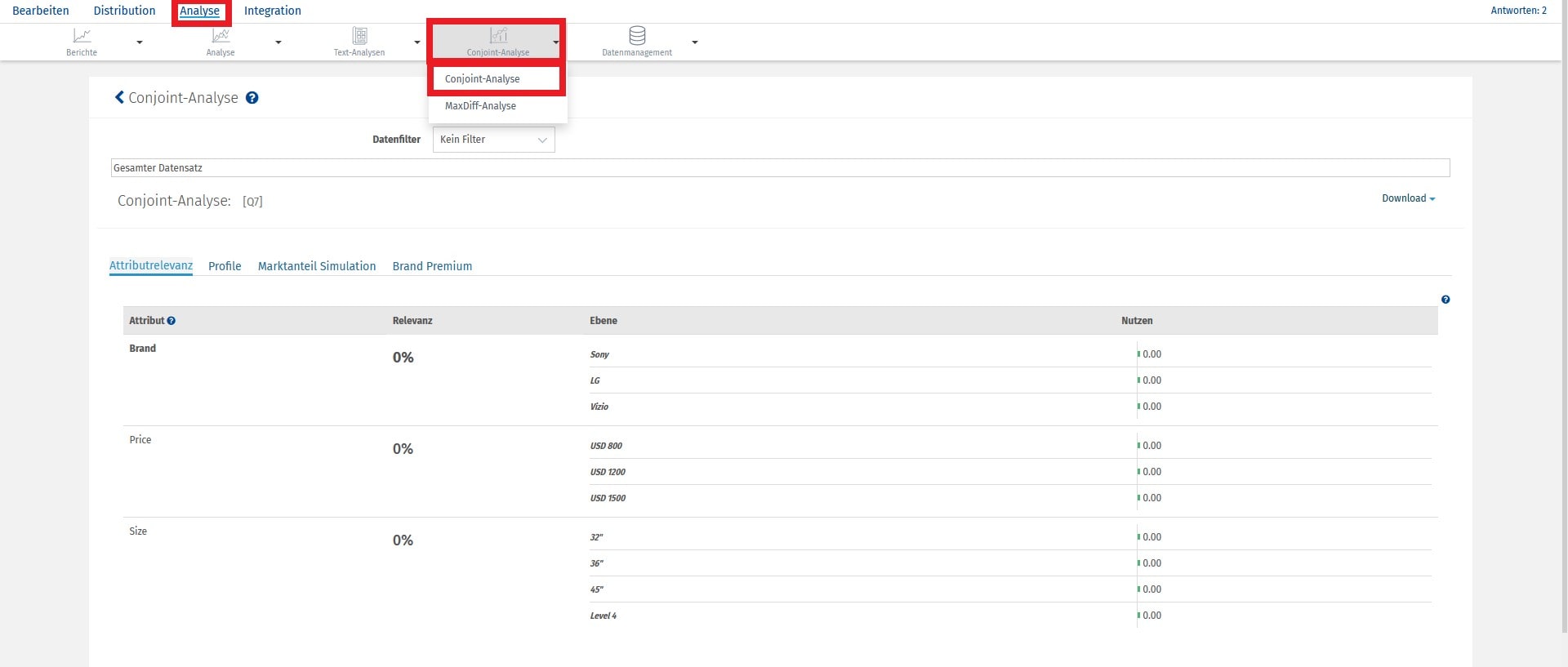
- Conjoint-Analyse - Bedeutung der Attribute
- Conjoint-Profile
- Marktanteil Simulation
- Conjoint-Analyse - Brand Premium
- Was ist MaxDiff Skalierung
- MaxDiff Einstellungen
- Anchored MaxDiff Analysis [BETA-Version]
- MaxDiff FAQ
- MaxDiff- Interpreting Results
- Automatischer E-Mail-Versand von Berichten
- Datenqualität - Gemusterte Antworten
- Datenqualität - gibberish words
- Externe Daten in neue Umfrage importieren
- Download-Center
- Berichte konsolidieren und zusammenfassen
- Befragungsdaten löschen
- Datenqualität - Alle Kontrollkästchen aktivieren
- Berichtexport in Word, Excel und PowerPoint
- Terminplaner
- Datenpad für eine Umfrage
- Merge Data 2.0
- Plagiatserkennung
- Umfrage-Ergebnisse exportieren in SPSS-Format
- Notification Group
- Unselected Checkbox Representation
- IP based location data
- SPSS variable name
- Benutzerprofil aktualisieren
- Zeitzone innerhalb des Umfragekontos ändern
- Geschäftsbereiche
- Organisationsübergreifendes Umfrage Konto
- Nutzungsdashboard
- E-Mail-Adresse für Support-Anfragen
- umfrage software lizenz vergleich
- Log-In - Fehlerbehebung
- Software-Unterstützung
- Welcome Email
- Benutzerrollen und Berechtigungen
- Viele Benutzer gleichzeitig hinzufügen
- Kontobestätigung: Zwei-Faktor-Authentifizierung
- Netzwerkzugang
- Navigating QuestionPro Products
- Changing ownership of the survey
- Unable to access Chat support
- Agency Partnership Referral Program
- Response Limits
- CAN-SPAM-Konformitätstool
- GDPR Compliance
- SAS 70 Typ II Sicherheit
- Sicherstellung der Anonymität der Befragten (RAA)
- Sicherheit
- Einhaltung des kalifornischen Verbraucherschutzgesetzes (CCPA)
- GDPR - right to be Forgotten
- QuestionPro Erklärung zur Zugänglichkeit
- Data Center
- Strong Password
- Automated deletion of data
Conjoint Teil-Wert-Berechnung
Wir verwenden den folgenden Algorithmus, um CBC Conjoint Teil-Wert-Berechnung zu berechnen:
- NOTATION
Es gibt R Befragte mit Individuen r = 1 ... R.
Lassen Sie jeden Befragten T Aufgaben mit t = 1 ... T haben
Lassen Sie jede Aufgabe t C-Konfigurationen (oder Konzepte) mit c = 1 ... C haben (C ist in unserem Fall normalerweise 3 oder 4)
Wenn wir A-Attribute haben, a = 1 bis A, wobei jedes Attribut La-Ebenen hat, l = 1 bis La, dann ist der Teilwert für a
bestimmtes Attribut / Niveau ist w '(a, l). Es ist dieses (gezackte Gitter) von Teilwerten, nach denen wir in dieser Übung suchen.
Vereinfachen Sie dies zu einem eindimensionalen Gitter w (s), in dem die Elemente sind:
{w '(1,1), w' (1,2) ... w '(1, L1), w' (2,1) ... w '(A, LA)} mit w mit S Elementen .Eine bestimmte Konfiguration x kann als eindimensionales Gitter x (s) dargestellt werden, wobei x (s) = 1 ist, wenn die spezifische Ebene / Attribut vorhanden ist, andernfalls 0.
Lassen Sie Xrtc die spezifische Konfiguration der c-ten Konfiguration in der t-ten Aufgabe für den r-ten Befragten darstellen.
Der Versuchsaufbau wird durch die vierdimensionale Matrix X mit der Größe RxTxCxS dargestellt
Wenn der Befragte r in Aufgabe t die Konfiguration c wählt, sei Yrtc = 1; sonst 0.
- NUTZEN EINER BESTIMMTEN KONFIGURATION
Das Dienstprogramm Ux einer bestimmten Konfiguration ist die Summe der Teilewerte für die in der Konfiguration vorhandenen Attribute / Ebenen, dh das Skalarprodukt xw
- DAS MULTI-NOMIALE LOGIT-MODELL
Für eine einfache Auswahl zwischen zwei Konfigurationen mit den Dienstprogrammen U1 und U2 sagt das MNL-Modell voraus, dass Konfiguration 1 ausgewählt wird
EXP (U1) / (EXP (U1) EXP (U2)) der Zeit (eine Zahl zwischen 0 und 1).
Für eine Auswahl zwischen N Konfigurationen wird Konfiguration 1 ausgewählt
EXP (U1) / (EXP (U1) EXP (U2) ... EXP (UN)) der Zeit.
- MODELLIERTE WAHLWAHRSCHEINLICHKEIT
Die Auswahlwahrscheinlichkeit (unter Verwendung des MNL-Modells) für die Auswahl der c-ten Konfiguration in der t-ten Aufgabe für den r-ten Befragten ist:
Prtc = EXP (xrtc.w) / SUMME (EXP (xrt1.w), EXP (xrt2.w), ..., EXP (xrtC.w))
- LOG-WAHRSCHEINLICHKEITSMAß
Das Log-Likelihood-Maß LL wird berechnet als:
Prtc ist eine Funktion des Teilwertvektors w, der die Menge der Teilwerte darstellt, nach denen wir suchen.
- LÖSUNG FÜR TEIL-WERTE MIT MAXIMALER WAHRSCHEINLICHKEIT
Wir lösen für den Teilwertvektor, indem wir den Vektor w finden, der den Maximalwert für LL ergibt. Beachten Sie, dass wir nach S-Variablen suchen.
Dies ist ein mehrdimensionales nichtlineares Problem der kontinuierlichen Maximierung und erfordert eine Standardlöserbibliothek. Wir verwenden den Nelder-Mead-Simplex-Algorithmus.
Die Log-Likelihood-Funktion sollte als Funktion LL (w, Y, X) implementiert und dann optimiert werden, um den Vektor w zu finden, der uns ein Maximum gibt. Die Antworten Y und das Design X sind gegeben und für eine spezifische Optimierung konstant. Anfangswerte für w können auf den Ursprung 0 gesetzt werden.
Die endgültigen Teilewerte w werden neu skaliert, so dass die Teilewerte für jedes Attribut einen Mittelwert von Null haben, indem einfach der Mittelwert der Teilewerte für alle Ebenen jedes Attributs subtrahiert wird.
- Login » Surveys » Reports » Choice Modelling » Conjoint Analysis