クロス集計とカイ二乗分析

この分析は、食事やカロリー消費に関して、十分な情報に基づいた決定を下すのに役立ちます。

クロス集計は、メインフレームの統計モデルであり、同じような行程をたどります。パターンや傾向、調査パラメータ間の相関関係を特定することで、リサーチャーが十分な情報に基づいた意思決定を行うのに役立ちます。研究を実施する際、ローデータは通常困難なものです。それらは常に、いくつかの混沌とした可能性のある結果を指し示します。そのような状況において、クロスタブは、研究内の相互に包括的な要因間の傾向、比較、相関を導き出すことによって、疑いなく単一の理論に集中するのに役立ちます。

例えば、大学受験を考えてみましょう。おそらくその時は気づいていなかったと思いますが、あなたは出願中に、志望する大学に関する意識的な決定を下すために、関係する要素を精神的にクロス集計していたのです。意思決定のプロセスを、1つずつ見ていきましょう。

まず学業面では、高校での成績、SATのスコア、専攻したい分野、出願エッセイを書く必要があります。次に、学費や奨学金の可能性を見る経済的な要素。最後に情緒的な要素で、自宅からの距離や、友人が検討している大学がどの程度遠いかを考慮します。言い換えれば、学業＋財務＋情緒のクロス集計によって、あなたは大学を絞り込むことができ、そのうちの1校があなたの母校になるか、または近いうちに母校になるのです。

クロス集計は、クロスタブまたは分割表とも呼ばれ、カテゴリーデータに使用される統計ツールです。カテゴリーデータには、互いに排他的な値が含まれます。データは常に数字で収集されますが、数字には意味がなければ価値はありません。例えば、リンゴ4個、バナナ7本、キウイ9個というように。

リサーチャーがクロス集計を使うのは、データ内の関係性を調べるためです。クロス集計は、市場調査やアンケート調査において非常に有用です。クロス集計レポートは、調査で尋ねられた2つ以上の質問間の関連性を示します。

例を用いたクロス集計の理解

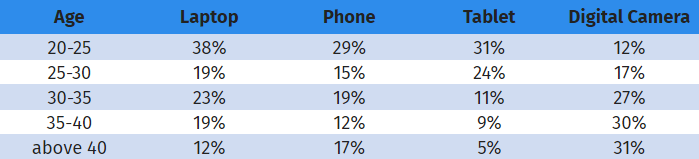
クロス集計は統計データ分析によく使われます。報告/分析ツールであるため、順序または名義など、どのようなデータレベルでも使用できます。すべてのデータを名義データとして扱います（名義データは測定されたものではなく、分類されたものです）。たとえば、年齢と電子機器の購入のような2つのカテゴリ変数の関係を分析できます。

ここで2つの質問があります：

• あなたの年齢はいくつですか?

• 今後半年以内に購入する可能性のある電子機器は何ですか？

この例では、年齢と電子機器の購入の間に特徴的な関係があることがわかります。収集されたデータを通して、2つの変数の相関関係を見ることは、驚くべきことではありませんが、エキサイティングなことです。

調査リサーチでは、クロス集計を使用することで、見込みデータを深く掘り下げて分析することができ、回答から収集したすべてのデータに圧倒されることなく、傾向や機会を簡単に見つけることができます。

クロス集計とカイ二乗

カイ二乗またはピアソンのカイ二乗検定は、リサーチャーが1つまたは複数のカテゴリにおいて、予想される度数と観察された度数の間に有意な差があるかどうかを判断するために使用する統計的仮説です。

調査結果をクロス集計する際に重要なことは、クロス集計の表現が真か偽かを検証することです。これは、私たちが大学に入った後に抱く、「これは本当に合っているのだろうか」という疑念に似ています。このジレンマを解決するために、クロスタブはカイ二乗分析とともに計算され、研究の変数が互いに独立しているか、関連しているかを識別するのに役立ちます。もし2つの要素が独立しているなら、その表は重要でないとされ、その研究は帰無仮説と呼ばれます。要素が互いに関連していないので、研究の結果は信頼できません。逆に、2つの要素の間に関係があれば、集計結果は有意であり、戦略的意思決定を行う上で信頼できることが確認できます。

ここで紹介するもう一つの重要な用語は、帰無仮説です。帰無仮説は、データセットに見られる差異や重要性は偶然によるものであると仮定します。帰無仮説の反対は対立仮説と呼ばれます。

調査へのカイ二乗の適用は、通常これらの質問タイプで行われます：

• 人口統計

• リッカート尺度の質問

• 都市

• 商品名

• 日付と番号（一緒にした場合）

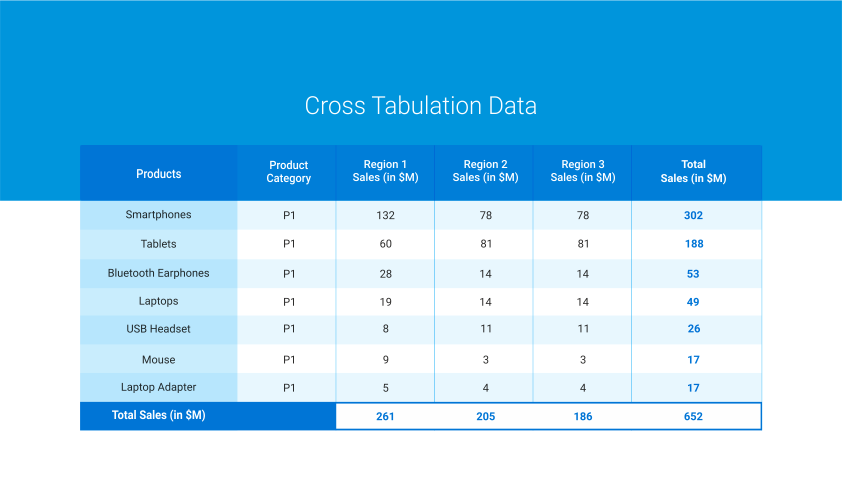
例えば、電子機器を購入する購買行動と、それが販売されている地域との間に関連性があるかどうかを調べる必要があります。データは下の表のように入力します：

前述のように、カイ二乗検定は、2つの離散変数が関連しているかどうかを決定するのに役立ちます。関連性がある場合、一方の変数の分布は、もう一方の変数の値によって異なります。しかし、2つの変数が独立であれば、1番目の変数の分布は、2番目の変数のすべての値で類似します。

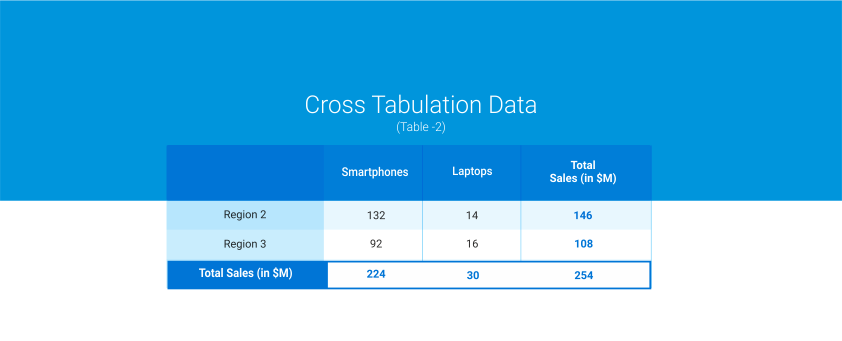
クロス集計とカイ二乗を用いて、我々は次の推論を導きます：

上記の値にカイ二乗計算を適用すると - ピアソンのカイ二乗= 0.803、 P-値= 0.05。これは何を意味するのでしょうか？p値に注目する必要があります。p-値を一般的に0.05であるアルファ・レベルと比較します。

• p-値がアルファ値以下であれば、2つの変数は関連しています。

• p-値がアルファ値より大きければ、変数は独立であると結論づけます。

この事例では、ピアソン カイ二乗統計量は、0.803（p値は0.05）です。したがって、アルファ値0.05では、相関がなく、重要でないと結論づけられます。

クロス集計とカイ二乗

• 調査でクロス集計を使用する大きな利点は、計算が簡単で非常に理解しやすいことです。リサーチャーがその概念について深い知識を持っていなくても、結果を解釈するのは簡単です。

• ローデータを理解し、解釈することは時に困難であるため、混乱を避けることができます。たとえ小さなデータセットであっても、データが整然と並べられていなければ混乱してしまうかもしれません。クロス集計は、データ表現に関連する混乱を最小限に抑えるのに役立つ変数を相関させる簡単な方法を提供します。

• クロス集計から多くの洞察を得ることができます。上のセクションのクロス集計の例で述べたように、ローデータを解釈するのは簡単ではありません。クロス集計は、変数間の相関をマップし、そうでなければ見落とされていたかもしれない洞察が明確に理解されます。統計の複雑な形式からの洞察を理解するのは簡単です。

• 複数の特徴にまたがる2つ以上の変数に関する適格な、または相対的なデータを簡単に提供します。

• 調査分析にクロス集計を使用する最も重要な利点は、データが名義、順序、区間、比率のいずれであっても簡単に使用できることです。

QuestionProを使用したクロス集計

1.QuestionPro アカウントにログインし、分析したいアンケートを選択します。

2.アナリティクスの下に「分析」のオプションがあります。分析」の下にある「クロス集計」をクリックします。

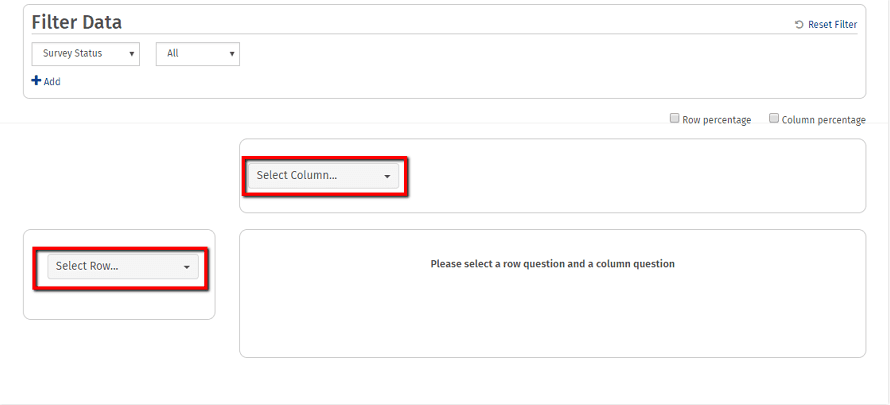
3.行の質問と列の質問をそれぞれドロップダウンから選択します。

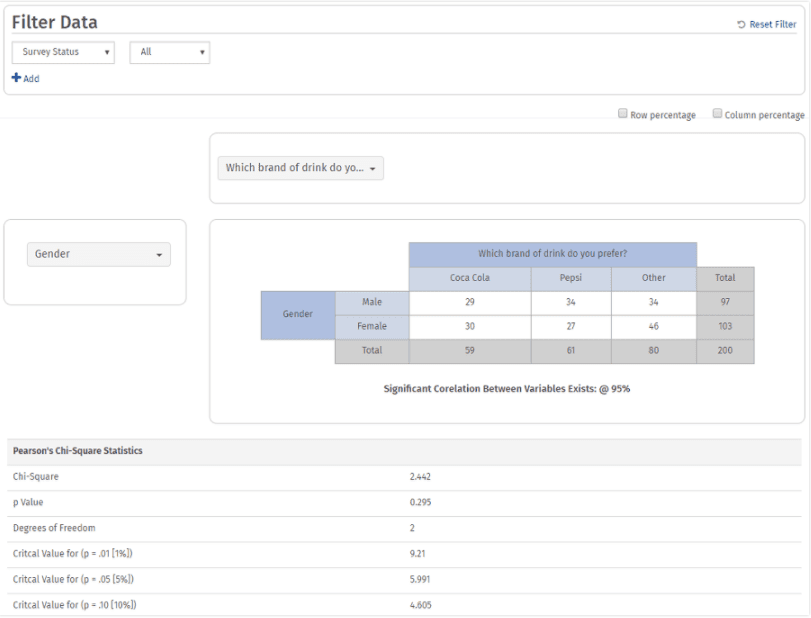
4.ピアソンのカイ二乗分析とともにクロス集計表が作成されます。

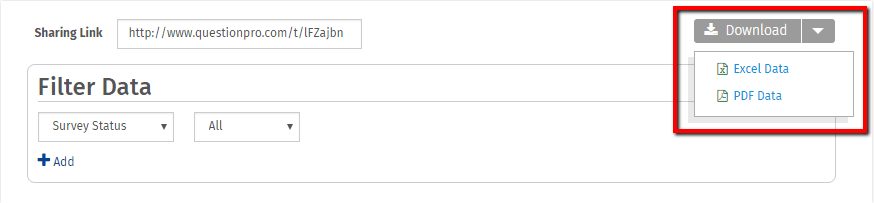
5.レポートを作成したら、レポートをダウンロードすることもできます。