Korrelationsanalyse

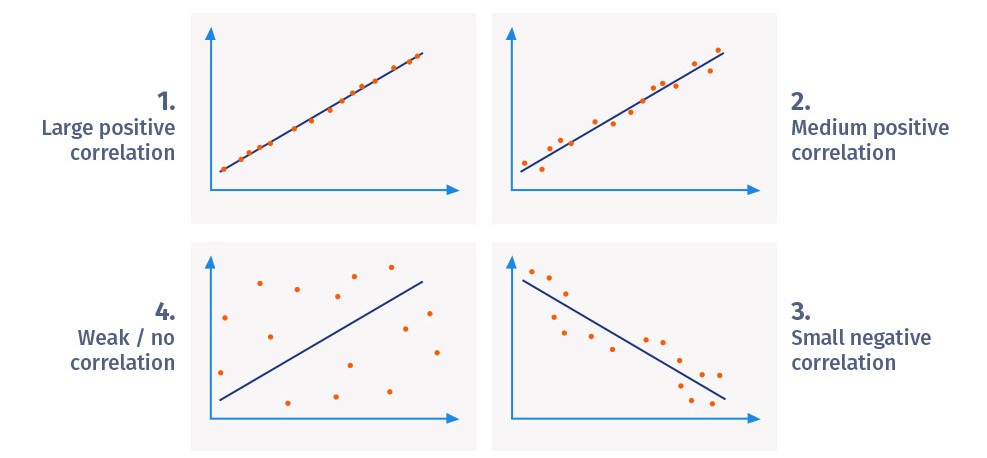
Eine hohe Korrelation weist auf eine starke Beziehung zwischen den beiden Variablen hin, während eine niedrige Korrelation bedeutet, dass die Variablen schwach miteinander verbunden sind.

Wenn es um Marktforschung geht, verwenden Forscher Korrelationsanalysen, um quantitative Daten zu analysieren, die durch Forschungsmethoden wie Umfragen und Live-Umfragen gesammelt werden. Sie versuchen, die Beziehungen, Muster, signifikanten Verbindungen und Trends zwischen zwei Variablen oder Datensätzen zu identifizieren.

Es besteht eine positive Korrelation zwischen zwei Variablen, wenn ein Anstieg einer Variablen zu einem Anstieg der anderen führt. Andererseits bedeutet eine negative Korrelation, dass, wenn eine Variable zunimmt, die andere abnimmt und umgekehrt.

Der Korrelationskoeffizient

Eines der statistischen Konzepte, das am meisten mit dieser Art der Analyse zu tun hat, ist der Korrelationskoeffizient.

Der Korrelationskoeffizient ist die Maßeinheit, die zur Berechnung der Intensität in der linearen Beziehung zwischen den an einer Korrelationsanalyse beteiligten Variablen verwendet wird. Dies ist leicht zu erkennen, da es mit dem Symbol dargestellt wird r und ist normalerweise ein Wert ohne Einheiten, der zwischen 1 und -1 liegt.

Beispiel einer Korrelationsanalyse

Die Korrelation zwischen zwei Variablen kann entweder eine positive Korrelation, eine negative Korrelation oder keine Korrelation sein. Schauen wir uns Beispiele für jeden dieser drei Typen an.

• Positive Korrelation: Eine positive Korrelation zwischen zwei Variablen bedeutet, dass sich beide Variablen in die gleiche Richtung bewegen. Eine Zunahme einer Variablen führt zu einer Zunahme der anderen Variablen und umgekehrt.

Wenn Sie beispielsweise mehr Zeit auf einem Laufband verbringen, werden mehr Kalorien verbrannt.

• Negative Korrelation: Eine negative Korrelation zwischen zwei Variablen bedeutet, dass sich die Variablen in entgegengesetzte Richtungen bewegen. Eine Zunahme einer Variablen führt zu einer Abnahme der anderen Variablen und umgekehrt.

Wenn Sie beispielsweise die Geschwindigkeit eines Fahrzeugs erhöhen, verkürzt sich die Zeit, die Sie benötigen, um Ihr Ziel zu erreichen.

• Schwach/Null-Korrelation: Es besteht keine Korrelation, wenn eine Variable die andere nicht beeinflusst.

Zum Beispiel gibt es keinen Zusammenhang zwischen der Anzahl der Schuljahre, die eine Person besucht hat, und den Buchstaben in ihrem Namen.

Verwendungen der Korrelationsanalyse

Korrelationsanalyse wird zur Untersuchung praktischer Fälle verwendet. Hier kann der Forscher einzelne Variablen nicht manipulieren. Mithilfe der Korrelationsanalyse wird beispielsweise die Korrelation zwischen dem Blutdruck des Patienten und den verwendeten Medikamenten gemessen.

Vermarkter nutzen es, um die Wirksamkeit von Werbung zu messen. Forscher messen den Anstieg/Rückgang des Umsatzes aufgrund einer bestimmten Marketingkampagne.

Vorteile der Korrelationsanalyse

In der Statistik bezieht sich Korrelation auf die Tatsache, dass zwischen verschiedenen Ereignissen ein Zusammenhang besteht. Eines der Werkzeuge, um festzustellen, ob ein solcher Zusammenhang besteht, ist die Korrelationsanalyse. Die praktische Einfachheit ist zweifellos einer der Hauptvorteile.

Um eine zuverlässige Korrelationsanalyse durchzuführen, ist es wichtig, zwei Variablen gründlich zu beobachten, was uns einen Vorteil bei der Erzielung von Ergebnissen verschafft. Zu den bemerkenswertesten Vorteilen der Korrelationsanalyse gehören:

• Bewusstsein über das Verhalten zwischen zwei Variablen: Eine Korrelation hilft dabei, das Fehlen oder Vorhandensein einer Beziehung zwischen zwei Variablen zu erkennen. Es ist tendenziell relevanter für den Alltag.

• Ein guter Ausgangspunkt für die Forschung: Es erweist sich als guter Ausgangspunkt, wenn ein Forscher zum ersten Mal mit der Untersuchung von Zusammenhängen beginnt.

• Verwendung für weitere Studien: Forscher können die Richtung und Stärke der Beziehung zwischen zwei Variablen identifizieren und die Ergebnisse später in späteren Studien eingrenzen.

• Einfache Metriken: Forschungsergebnisse sind einfach zu klassifizieren. Die Befunde können zwischen -1,00 und 1,00 liegen. Es kann nur drei mögliche allgemeine Ergebnisse der Analyse geben.

Wie nutzen Sie die Korrelationsanalyse in Ihren Umfragen?

Erfahren Sie mit unserem wie Sie diese Funktion einrichten und verwenden Hilfedatei zur Korrelationsanalyse.